Tablice

Pewien restaurator, przyjmując zamówienia na ekskluzywne bankiety, prosił klientów o przysłanie spisu gości z zaznaczeniem, kto ma koło kogo siedzieć. Oto jeden z takich spisów:

Bankiet klubu "Biały Mankiet"

Przed bankietem kierownik sali ustalał liczbę potrzebnych stołów. Na przykład, by usadzić gości według powyższego spisu, potrzeba jednego stołu dla gości o numerach 0, 4 i 8, drugiego stołu dla gości o numerach 3, 2 i 1 oraz trzeciego stołu dla gości o numerach 5, 7, 6 i 9. Zaszła jednak seria nieprzyjemnych pomyłek, w wyniku której restaurator stracił zaufanie do kierownika sali i postanowił zamówić program komputerowy obliczającym m.in. liczbę potrzebnych stołów.

Zadanie bankiet

Dane: spis gości ponumerowanych kolejnymi liczbami naturalnymi ze wskazaniem numeru prawego sąsiada.

Wynik: liczba stołów.

Kierownik sali miał swoje sprawdzone metody wyznaczania liczby stołów. Przenosił spis na kartkę (same numery z pominięciem nazwisk) i rysował relację "bycia prawym sąsiadem". Zaczynał od takiego rysunku:

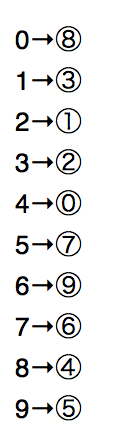
następnie zaznaczał sąsiedztwo i od razu wychodziła mu potrzebna liczba stołów:

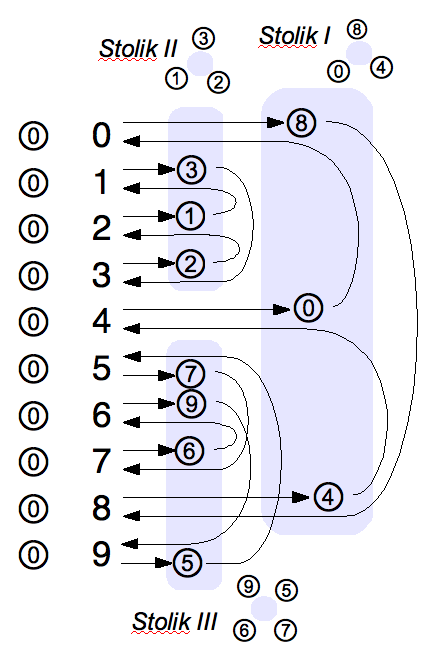
Konkretnie to robił to tak, że schodził po kolejnych wierszach od góry. Jeżeli znalazł osobę nie usadzoną przy stoliku, to zaznaczał, że potrzebny jest jeszcze jeden stolik i przechodząc po strzałkach wykreślał kolejnych sąsiadów. Po "obejściu stolika" lądował w tym wierszu, w którym rozpoczął "obchód" i kontynuował przeglądanie tabeli w dół. Zatrudniony konsultant-programista sformułował ten algorytm następująco:

 liczbaStolow = 0
 k = 0
 dopóki k < liczba gości
     jeżeli gość k nie jest usadzony
         liczbaStolow = liczbaStolow + 1
         powtarzaj, co następuje:
             wykreśl usadzonego gościa k
             k = prawy sąsiad k
         dopóki gość k nie jest gościem już skreślonym
     k = k + 1

Wydawałoby się, że dalej będzie z górki, ale na pierwszą trudność napotykamy już przy próbie zapisania nagłówka funkcji:

def policzStoly(sasiadGoscia0, sasiadGoscia1, sasiadGoscia2)

W ten sposób moglibyśmy obsłużyć dowolną, ale ustaloną liczbę gości (tutaj trzech). Takie rozwiązanie zastosowaliśmy np. w programie wyznaczającym najlżejszy z trzech odważników. Tu jednak liczba gości nie jest z góry znana.

Z matematycznego punktu widzenia spis gości, a w zasadzie tylko jego "liczbowa" część (nazwiska nas na razie nie interesują), to tzw. ciąg skończony. W naszym przypadku ta funkcja dla numeru gościa podaje numer sąsiada z prawej strony. W programowaniu skończone ciągi reprezentujemy za pomocą tzw. tablic.

W języku Python ciągami posługujemy się tak:

• [1, 1, 2, 5, 8] - utworzenie wektora o zadanych elementach (czyli inaczej ciągu o zadanych wyrazach),
• s[n] - indeksowanie, czyli pobranie n-tego elementu ciągu (n-tego wyrazu ciągu),
• s[n] = x - modyfikacja ciągu, polegająca na podmianie n-tego elementu na x,
• len(s) - wyznaczenie liczby elementów ciągu (czyli długości ciągu)

Teraz przynajmniej wiemy, jak zacząć:

def policzStoly(sasiedztwo):
    liczbaStolow = 0
    k = 0
    while k < len(sasiedztwo):
        ...
        k = k+1
    return liczbaStolow

Kierownik sali skreślał usadzonych gości, dzięki czemu obchodził każdy stolik tylko jeden raz. W jaki sposób "skreślić" element wektora? Możemy skorzystać z faktu, że wszystkie elementy wektora są nieujemne i umówić się, że jeżeli zamiast numeru sąsiada figuruje np. liczba -1, to gość jest skreślony. Wykorzystamy ten pomysł w poniższym programie:

def policzStoly(sasiedztwo):
    SKRESLONY = -1
    liczbaStolow,k = 0,0
    while k < len(sasiedztwo):
        if sasiedztwo[k] != SKRESLONY:
            assert 0 <= k < len(sasiedztwo)
            liczbaStolow = liczbaStolow + 1
            while True:
                kolejny = sasiedztwo[k]
                sasiedztwo[k] = SKRESLONY
                k = kolejny
                if sasiedztwo[k] == SKRESLONY: break
        k = k+1
    return liczbaStolow

Pętla zewnętrzna przebiega kolejne wiersze tabeli. Instrukcja if odpowiada pomijaniu tych gości, którzy zostali już usadzeni (skreśleni), a pętla wewnętrzna "obchodzi" stoliki, wykreślając gości. Pętla zewnętrzna jest tak skonstruowana, by jednym z jej niezmienników był warunek:

wszyscy goście o numerach mniejszych od k są usadzeni (skreśleni).

Kolejnym istotnym niezmiennikiem zewnętrznej pętli jest warunek:

wartość zmiennej liczbaStolow jest liczbą stołów potrzebną i wystarczającą do usadzenia wszystkich gości o numerach mniejszych od k, przy zachowaniu sąsiedztwa wymaganego w spisie gości .

Oba te niezmienniki gwarantują nam poprawność rozwiązania.

Zadanie minimum

Dane: skończony, niepusty ciąg \(n\) liczb \(a_0\), \(a_2\), ... \(a_{n-1}\) dany w postaci wektora A.

Wynik: wartość najmniejszego elementu ciągu.

Z problemem wyszukiwania minimum spotykamy się w życiu codziennym, np. grając w karty. Zasady konkretnej gry określają "starszeństwo" kart (np. że dwójka kier jest "słabsza" od trójki kier, walet pik jest "słabszy" od damy pik). Mając w ręku karty z rozdania przeglądamy je próbując znaleźć najsłabszą. Zazwyczaj robi się to w ten sposób, że przegląda się karty np. od lewej do prawej, pamiętając dotychczas najsłabszą, znalezioną dotąd kartę. Po dojściu do ostatniej (skrajnie prawej) karty wiemy, która karta jest najsłabsza spośród wszystkich kart w ręce. Ta prosta metoda opiera się na fakcie, że przeglądając karty utrzymujemy niezmiennik: zapamiętana karta jest najsłabsza z dotychczas przejrzanych.

Algorytm możemy zapisać w ten sposób:

    zmiennej m przypisz wartość pierwszego elementu ciągu
    dopóki zostały jeszcze jakieś elementy
        jeżeli wartość kolejnego elementu ciągu jest mniejsza od wartości zmiennej m, przypisz tę wartość na zmienną m
    wartość m to poszukiwane minimum

Opis możemy uściślić wprowadzając zmienną k przebiegającą kolejne elementy ciągu:

    niech m = A[0]
    niech k = 1
    dopóki k < n:
        jeśli A[k] < m:
            niech m równa się A[k]
        zwiększ k o jeden
    zwróć m

Niezmiennik - "zapamiętana karta jest najsłabsza z dotychczas przejrzanych" - możemy teraz wyrazić w ten sposób: wartość m jest najmniejsza w ciągu A[0], A[1], ..., A[k-1].

Powyższy warunek (niezmiennik) zachodzi każdorazowo po sprawdzeniu dozoru pętli. Ciało pętli jest skonstruowane w ten sposób, żeby posuwać pracę do przodu poprzez zwiększanie wartości k, ale by jednocześnie nie popsuć niezmiennika - o niezmiennik "troszczy się" instrukcja warunkowa wewnątrz pętli.

Dzięki niezmiennikowi mamy pewność, że po zakończeniu wykonywania pętli wartość zmiennej m, to minimum z liczb A[0], ..., A[k-1]. Skąd jednak wiadomo, że A[0],...,A[k-1] to cały ciąg A? Innymi słowy, skąd wiadomo, że po zakończeniu pętli k==n ?

Pętla while gwarantuje, że po zakończeniu jej wykonywania prawdziwa jest negacja dozoru, czyli "nie prawda, że \(k < n\)", czyli \(k \ge n\). Prawie o to chodziło, mamy zagwarantowane, że \(k \ge n\), czyli że na pewno wszystkie elementy ciągu A są uwzględnione przy wyznaczeniu wartości minimum. Pozostaje jednak pewien niesmak: przecież widać, że na koniec \(k == n\). Jak to udowodnić?

Na każdą równość można patrzeć, jak na dwie nieostre nierówności: zdanie \(k==n\) jest równoważne koniunkcji \(k \ge n\) oraz \(k \le n\). Widać, że brakuje nam uzasadnienia dla "połowy" tego warunku: chcielibyśmy pokazać, że po zakończeniu pętli nie tylko \(k \ge n\), ale też że \(k \le n\).

Niezmiennik to dowolne zdanie logiczne, które jest prawdziwe każdorazowo po sprawdzaniu dozoru pętli. Każda pętla ma bardzo wiele niezmienników, niektóre są przydatne, niektóre są bez sensu. Może wśród niezmienników naszej pętli jest jakiś, który uzasadnia nierówność \(k \le n\) ?

Nie trzeba daleko szukać, w istocie samo zdanie \(k \le n\) to jeden z niezmienników. Jedyną instrukcją, która mogłaby popsuć niezmiennik \(k \le n\) jest zwiększenie \(k\) o jeden w pętli. Na szczęście dozór pętli gwarantuje, że to zwiększenie wykonywane jest wyłącznie pod warunkiem \(k < n\). Ostrość nierówności gwarantuje, że wartość \(k\) powiększona o jeden nie przekroczy wartości \(n\). Zauważmy przy tym, że warunek niepustości ciągu nałożony na dane wejściowe jest bardzo ważny - bez niego zdanie \(k \le n\) nie byłoby spełnione dla ciągu pustego (zmienną \(k\) ustawiamy początkowo na 1, a przy ciągu pustym \(n==0\)).

Reasumując, dwa ważne niezmienniki to:

• wartość \(m\) jest najmniejsza w ciągu A[0], A[1], ..., A[k-1],
• \(k \le n\).

Te niezmienniki gwarantują, że po zakończeniu wykonania pętli mamy:

• wartość \(m\) jest najmniejsza w ciągu A[0], A[1], ..., A[k-1] (niezmiennik),
• \(k \le n\) (niezmiennik),
• \(k \ge n\) (negacja dozoru).

czyli, że wartość zmiennej \(m\) jest najmniejsza w ciągu A[0], A[1], ..., A[k-1] (niezmiennik) i \(k == n\), a stąd wartość \(m\) jest
najmniejsza w całym ciągu A. I o to chodziło!

Zadanie wyszukiwanie liniowe

Dane: skończony ciąg \(n\) liczb \(a_0\), \(a_2\), ... \(a_{n-1}\) dany w postaci wektora A oraz wartość x.

Wynik: indeks pod którym wartość x występuje w ciągu A (czyli liczba k taka, że A[k] = x) lub -1, jeżeli x nie występuje w ciągu A.

Wyszukiwanie elementu to kolejny elementarny problem, który częściej pojawia się w rozwiązaniach innych problemów, niż jako zadanie samo w sobie.

Podobnie jak przy wyznaczaniu minimum możemy przeglądać kolejne elementy wektora. W tym jednak przypadku nie musimy tego robić do końca. Jeżeli element x się znajdzie, to wykonywanie pętli można przerwać.

    niech k = 0
    dopóki k < n:
        jeżeli A[k] == x, zwróć k
        zwiększ k o jeden
    zwróć -1

Istotnym niezmiennikiem pętli jest warunek: przejrzane elementy wektora A nie zawierają elementu x.

Bardziej precyzyjnie możemy go zapisać tak: elementy A[0], ..., A[k-1] nie zawierają elementu x.

Zauważmy, że w powyższym algorytmie wykonywanie pętli może zakończyć się z dwóch powodów. Po pierwsze, jeżeli wartość k osiągnie koniec wektora (czyli, gdy k zrówna się z n), to dozór przestanie być spełniony i wykonanie pętli zakończy się. Po drugie, może nastąpić wymuszone wyjście z pętli, jeżeli znajdziemy x. W drugim przypadku poprawność nie pozostawia wątpliwości - znaleźliśmy k takie, że A[k]==x i już. W pierwszym przypadku, po wyjściu z pętli mamy zagwarantowane spełnienie następujących warunków:

• elementy A[0], ..., A[k-1] nie zawierają x (niezmiennik),
• k <= n (niezmiennik),
• k >= n (negacja dozoru).

czyli elementy A[0], ..., A[k-1] nie zawierają x i k == n, a co za tym idzie elementy wektora A nie zawierają x.
W takim przypadku możemy z czystym sumieniem zwrócić wartość -1, oznaczającą brak wystąpień x.

ZADANIA

Zadanie 1

Zakoduj algorytm wyszukiwania liniowego jako funkcję "wyszukaj".

Rozwiązanie:

def wyszukaj(A, x):
    k = 0;
    while k < len(A):
        if A[k] == x: return k;
        k = k+1;
    return -1;

Zadanie 2*

Pętle przebiegające ciągi: W wielu przypadkach kod wykorzystujący pętle do operacji na ciągach ma na przykład postać:

k = 0
while k < len(A):
    ... zrób coś z A[k] ...
    k = k+1

Wiele języków programowania oferuje specjalne postaci pętli upraszczające ten zapis:

for x in A:
    ... zrób coś z x ...

Zapisz rozwiązanie zadania minimum za pomocą pętli for.

Rozwiązanie:

def minimum(A):
    m = A[0]
    for x in A:
        if m < x: m = x
    return m

Zadanie 3

Okazuje się, że odpowiedzialność za wpadkę ponosi nie tylko kierownik sali. W spisie gości był błąd, oto początkowy fragment wektora opisującego sąsiadów:

s[0]=4, s[1]=7, s[2]=0, s[3]=2, s[4]=3, s[5]=1, s[6]=4, s[7]=15, s[8]=6, s[9]=26, s[10]=8.

Wynika z niego, że zarówno zero, jak i szóstka mają czwórkę za prawego sąsiada. Zmodyfikuj program i dopisz odpowiednie asercje, by zapobiec zwróceniu niepoprawnego wyniku w sytuacji, gdy dane wejściowe są niepoprawne (funkcja która otrzyma niepoprawne dane powinna zakończyć się z powodu niespełnienia warunku asercji).

Rozwiązanie:

def policzStoly(sasiedztwo):
    SKRESLONY = -1
    liczbaStolow,k = 0,0
    while k < len(sasiedztwo):
        if sasiad[k] != SKRESLONY:
            assert 0 <= k < len(sasiedztwo)
            liczbaStolow = liczbaStolow + 1
            m = k
            while True:
                kolejny = sasiedztwo[m]
                sasiedztwo[m] = SKRESLONY
                m = kolejny
                if sasiedztwo[m] == SKRESLONY: break
             assert k == m #niespełniona asercja, to zły spis
        k += 1
    return liczbaStolow

Zadanie 4

Co by się zmieniło, gdyby algorytm wyszukiwania najmniejszego elementu zapisać tak:

    niech m równa się A[0]
    niech k równa się 1
    dopóki k < n:
        jeśli A[k] < m:
            niech m równa się A[k]
        w przeciwnym przypadku:
            zwiększ k o jeden
    zwróć m

Rozwiązanie:

W zasadzie nic, program dawałby takie same wyniki, ale byłby mniej czytelny, a także pętla obracałaby się więcej razy. To nie jest zmiana na lepsze.

Zadanie 5

Napisz program, który w niepustym ciągu A znajduje pozycję elementu o wartości minimalnej.

Rozwiązanie:

Zauważ, że w ciągu może być kilka elementów o wartości minimalnej, na przykład w ciągu [1,3,1,5] mamy dwie jedynki. Przy tak sformułowanym zadaniu zakładamy zazwyczaj, że chodzi o znalezienie pozycji dowolnego elementu o wartości minimalnej. Zleceniodawca nie precyzuje, o który dokładnie element chodzi, więc mamy prawo napisać program tak, jak nam wygodnie.

def pozycjaMinimum(A):
    assert len(A) > 0
    k = 1
    p = 0
    while k < len(A):
        if A[k] < A[p]:
            p = k
        k = k + 1
    return p

Zadanie 6

Jeśli chcielibyśmy funkcję "minimum" zmienić w funkcję "maksimum", to jakich zmian należałoby dokonać w kodzie?

Rozwiązanie:

Należy (a) zmienić nazwę funkcji, (b) zmienić zwrot nierówności w instrukcji warunkowej.

Zadanie 7

Udowodnij, że algorytm podany jako rozwiązaniezadania wyszukiwania liniowego znajduje pierwsze wystąpienie x w wektorze A.

Zadanie 8

Zaprojektuj i zakoduj algorytm, który znajduje ostatnie wystąpienie liczby x w wektorze A.

Zadanie 9

Zaprojektuj i zakoduj algorytm, który policzy ile razy dana liczba x występuje w danym wektorze A.