Informatyka MIMUW

W niniejszym wykładzie wszystkie rozważane przestrzenie są skończenie wymiarowe a bazy są uporządkowane.

Macierz odwzorowania liniowego

Niech dane będą przestrzenie wektorowe $V$ i $W$ nad ciałem $\mathbb K$ oraz odwzorowanie liniowe $f:V\longrightarrow W$.

Niech $e_1,...,e_n$ będzie bazą przestrzeni wektorowej $V$, zaś $e'_1,...,e'_m$ bazą przestrzeni $W$. Dla odwzorowania liniowego $f$ mamy

$\begin{array} {rcl} &&f(e_1) =a_{11}e'_1+... +a_{m1}e'_m,\\ &&\ \ \ .\\ &&\ \ \ .\\ &&\ \ \ .\\ &&f(e_n)= a_{1n}e'_1+...+a_{mn}e'_m. \end{array}$      (1.1)

dla pewnych skalarów $a_{ij}$, $i=1,...,m$, $j=1,...,n$. Inaczej zapisując

dla każdego $j=1,...,n$.

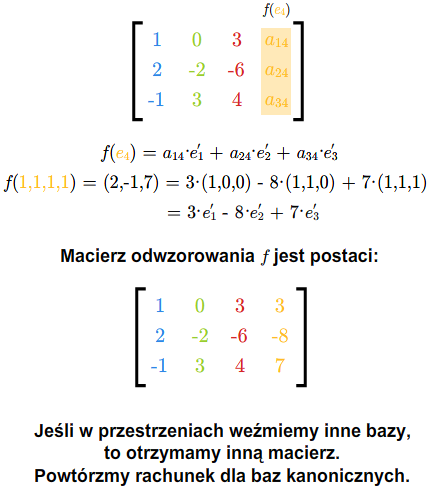
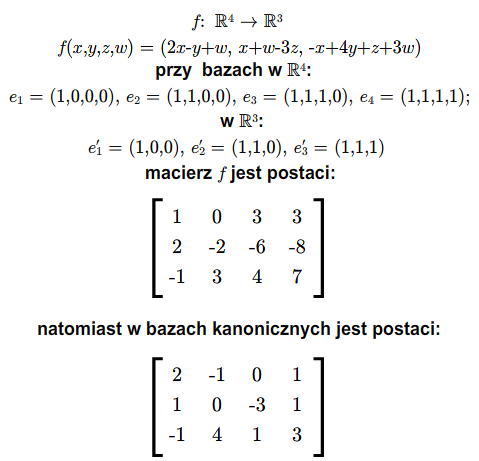
Otrzymaliśmy więc macierz $A=[a_{ij}]_ {\tiny\begin{array} {l} 1\le i\le m\\ 1\le j\le n \end{array} }$, która całkowicie opisuje odwzorowanie liniowe $f$. Istotnie, jeśli znamy wartości odwzorowania liniowego na bazie, to znamy to odwzorowanie. Macierz tę nazywamy macierzą odwzorowania $f$ przy bazach $e_1,...,e_n$ i $e'_1,...,e'_m$.

Jeśli mamy daną macierz $A$, ustalone bazy w przestrzeniach $V$, $W$, to macierz ta jest macierzą odwzorowania liniowego $f:V\longrightarrow W$. Odwzorowanie to jest dane formułą (1.1).

Wygodnie jest myśleć o macierzach jako o odwzorowaniach liniowych. Jeśli żadne szczególne przestrzenie nie są wyróżnione, to macierz $A=A_{m\times n}$ możemy traktować jako odwzorowanie liniowe $f:\mathbb K ^n\longrightarrow \mathbb K^m$ dane przepisem (1.1), gdzie $e_1,...,e_n$ jest bazą kanoniczną przestrzeni $\mathbb K ^n$, zaś $e'_1,...,e'_m$ jest bazą kanoniczną przestrzeni $\mathbb K ^m$.

Jeśli $A$ jest macierzą odwzorowania $f:V\longrightarrow W$ i przez $A_1,..., A_n$ oznaczymy kolumny macierzy $A$, to każda kolumna $A_j$ jest ciągiem współrzędnych wektora $f(e_j)$ w bazie $e'_1,..., e'_m$. Oznacza to, że układ kolumn macierzy $A$ można uważać za wektory (wyrażone we współrzędnych w bazie $e_1,...,e_n$) $f(e_1),...,f(e_n)$. Rząd odwzorowania $f$ jest więc rzędem układu wektorów $A_1,..., A_n$ macierzy $A$.

Mamy więc

Twierdzenie 1.1

Jeśli $A$ jest macierzą odwzorowania $f:V\longrightarrow W$ przy pewnych bazach przestrzeni $V$ i $W$, to $rk A= rk f$.

Niech $f,h :V\longrightarrow W$ będą dwoma odwzorowaniami liniowymi. Wiemy, że suma tych odwzorowań jest odwzorowaniem liniowym. Przy danych bazach $e_1,...,e_n$, $e'_1,...,e'_m$ przestrzeni $V$ i $W$ odpowiednio, macierz odwzorowania $f+h$ jest sumą macierzy $A_f+A_h$, gdzie $A_f$ jest macierzą odwzorowania $f$ a $A_h$ macierzą odwzorowania $h$. A zatem dodawanie macierzy odpowiada dodawaniu odwzorowań liniowych. Podobnie mnożeniu macierzy przez skalar odpowiada mnożenie odwzorowania liniowego przez skalar.

Załóżmy teraz, że mamy trzy przestrzenie wektorowe $V$, $W$, $U$. Załóżmy ponadto, że $e_1,...,e_n$ jest bazą $V$, $e'_1,...,e'_k$ jest bazą $W$ i $e''_1,...,e''_m$ jest bazą $U$. Niech $f:V\longrightarrow W$ i $h:W\longrightarrow U$ będą odwzorowaniami liniowymi. Oznaczmy przez

macierze odwzorowania $f$, $h$ i $h\circ f$ odpowiednio, przy danych bazach. Zachodzą następujące równości

Z drugiej strony

Zatem

Oznacza to, że

Krótko mówiąc, mnożenie macierzy odpowiada składaniu odwzorowań liniowych. Ponieważ składanie odwzorowań jest łączne, więc mnożenie macierzy jest łączne. Wspomnieliśmy już tę własność w poprzednim wykładzie. Teraz uzasadniliśmy jej prawdziwość.

Zauważmy także, że jeśli $h_1, h_2: W\longrightarrow U$, to $(h_1+h_2)\circ f= h_1\circ f +h_2\circ f$. Jeśli $f_1, f_2:V\longrightarrow W$, to $h\circ (f_1+f_2)=h\circ f_1 +h\circ f_2$. W języku macierzy oznacza to, że $(B_1 +B_2)A=B_1A+B_2A$ oraz $B(A_1+A_2)=BA_1+BA_2$ (jeśli występujące tu dodawania i mnożenia macierzy można wykonać). Te własności rachunku macierzy również wymieniliśmy w poprzednim wykładzie.

Macierz dualna i odwzorowanie dualne

Niech $e^*_1,..., e^*_n$ będzie bazą dualną do bazy $e_1,...,e_n$ przestrzeni $V$ i $e'^*_1,...,e'^*_m$ bazą dualną do bazy $e'_1,...,e'_m$ przestrzeni $W$. Rozważmy odwzorowanie dualne $f^*:W^* \longrightarrow V^*$. Chcemy znaleźć macierz $f^*$ przy wyróżnionych właśnie bazach dualnych. Oznaczmy poszukiwaną macierz przez $B=[b_{ji}]_ {\tiny\begin{array} {l} 1\le j\le n\\ 1\le i\le m \end{array} }$, czyli

Po obydwu stronach powyższej równości mamy wektory z $V^*$, czyli odwzorowania liniowe określone na $V$ i o wartościach w $\mathbb K$. Obliczymy wartość tych odwzorowań na wektorach bazy $e_1,..., e_n$. Otrzymujemy

Z drugiej strony

A zatem $a_{is}=b_{si}$, co oznacza, że macierz $B$ jest macierzą dualna do macierzy $A$.

Macierz odwzorowania dualnego jest macierzą dualną do macierzy odwzorowania danego, jeśli w przestrzeniach dualnych wybierzemy bazy dualne.

Stąd, że dla odwzorowań liniowych zachodzi formuła $(f \circ h)^* = h^* \circ f^*$, otrzymujemy analogiczną formułą dla macierzy.

Twierdzenie 2.1

Jeśli iloczyn $AB$ jest wykonalny, to wykonalny jest iloczyn $B^* A^*$ oraz

Udowodnimy teraz następujące twierdzenie

Twierdzenie 2.2

Rząd odwzorowania dualnego do $f$ jest równy rzędowi odwzorowania $f$.

Dowód

Wiemy, że

$rk f^*=\dim W^*-\dim ker f^*=\dim W-\dim\ker f^*.$      (2.2)

Przyjrzyjmy się więc przestrzeni $\ker f^*$. Mamy

Weźmy bazę $w_1,...,w_k$ przestrzeni $im f$. Jeśli $im f= W$, to $rk f=\dim W$ i $\ker f^*= \{0\}$. Twierdzenie w tym przypadku jest prawdziwe..

Jeśli $im f\ne W$, to układ $w_1,...,w_k$ rozszerzmy do bazy

przestrzeni $W$. Przestrzeń $U$ rozpięta na wektorach $w_{k+1},...,w_m$ jest dopełnienieniem algebraicznym do $im f$ w $W$, czyli $W=U\oplus im f$. Zauważmy, że odwzorowanie

jest izomorfizmem. Oczywiście odwzorowanie $\phi$ jest liniowe. Jeśli $\phi(\beta)=0$, to $\beta_{|U}$ i $\beta _{| im f}$ są odwzorowaniami zerowymi. A zatem, $\beta$ jest odwzorowaniem zerowym na całym $W$. Odwzorowanie $\phi$ jest więc monomorfizmem.

Jest też epimorfizmem. Jeśli bowiem $\gamma :U\longrightarrow \mathbb K$ jest liniowe, to odwzorowanie liniowe $\beta: W\longrightarrow \mathbb K$ zdefiniowane na bazie przestrzeni $W$ następująco: $\beta (w_i)=0$ dla $i=1,...,k$,$\beta (w_i)=\gamma (w _i)$ dla $i=k+1,..., m$, jest takie, że $\phi (\beta)=\gamma$.

Ponieważ $\phi$ jest izomorfizmem, więc $\dim\ker f^* = \dim U ^* =\dim U =m-k =\dim W- rk f$. Porównując tę równość z równością z pierwszego zdania tego dowodu otrzymujemy żądaną tezę.

Z powyższego twierdzenia i stąd, że macierz odwzorowania dualnego jest macierzą dualną do macierzy odwzorowania danego wynika następujący wniosek

Wniosek 2.3

Dla dowolnej macierzy $A$ zachodzi równość $rk A= rk A^*$.

Przypomnijmy sobie teraz operacje dopuszczalne na macierzy (ze względu na rząd macierzy). Korzystając z równości ${rk} A={rk} A^*$ dostajemy natychmiast kilka kolejnych operacji dopuszczalnych, tzn. nie zmieniających rzędu macierzy. Mianowicie, dodając do danego wiersza macierzy $A$ kombinację liniową pozostałych wierszy tej macierzy, nie zmieniamy jej rzędu. Mnożąc dowolny wiersz przez niezerowy skalar nie zmieniamy rzędu macierzy. I wreszczcie, permutując wiersze macierzy nie zmieniamy jej rzędu.

Tak jak w dowodzie twierdzenia o istnieniu bazy z Wykładu 2. możemy stwierdzić, że rząd skończonego układu wektorów jest równy maksymalnej liczbie wektorów liniowo niezależnych, które można wybrać z danego układu wektorów.

A zatem mamy następujące twierdzenie

Twierdzenie 2.4 [Rząd macierzy]

Niech $A\in M(m,n;\mathbb K)$.

1. Rząd macierzy A jest równy maksymalnej liczbie kolumn liniowo niezależnych, które można wybrać z macierzy $A$.
2. Rząd macierzy A jest równy maksymalnej liczbie wierszy liniowo niezależnych, które można wybrać z macierzy $A$.

Macierz odwrotna, ogólna grupa liniowa

Załóżmy teraz, że $V=W$ i $f:V\longrightarrow V$ jest endomorfizmem. Wybieramy jedną bazę, tzn. bazę $e_1,...,e_n$ przestrzeni $V$, i definiujemy macierz kwadratową $A=[a_{ij}]_ {\small 1\le i,j\le n}$ formułą

Ponieważ mnożenie macierzy odpowiada składaniu odwzorowań, więc odwracalność macierzy $A$ jest równoważna izomorficzności odwzorowania $f$. Ponadto macierz odwrotna $A^{-1}$ do macierzy $A$ jest macierzą odwzorowania odwrotnego $f^{-1}$.

Ogólną grupę liniową $GL(n;\mathbb K)$ możemy traktować jako grupę wszystkich izomorfizmów liniowych $f:\mathbb K^n\longrightarrow\mathbb K^n$, z działaniem będącym składaniem odwzorowań. Pamiętamy, że grupa ta dla $n>1$ jest nieprzemienna. Zauważyliśmy już, że macierz kwadratowa $A$ jest odwracalna wtedy i tylko wtedy, gdy jest macierzą izomorfizmu. Odwzorowanie liniowe $f:\mathbb K ^n\longrightarrow \mathbb K^n$ jest izomorfizmem wtedy i tylko wtedy, gdy $rk f=n$. Oznacza to, że prawdziwe jest następujące twierdzenie

Twierdzenie 3.1

Macierz kwadratowa $A=A_{n\times n}$ jest odwracalna wtedy i tylko wtedy, gdy $rk A=n$.

Macierz przejścia

Niech $e_1,...,e_n$ będzie bazą przestrzeni $V$ i niech $e'_1,..., e'_n$ będzie inną bazą tej samej przestrzeni. Istnieją jednoznacznie określone skalary $p_{ij}$, $1\le i,j\le n$, takie, że

$\displaystyle e'_j=\sum _{i=1}^n p_{ij}e_i,$      (4.4)

dla $j=1,...n$. Macierz $P=[p_{ij}]_{1\le i, j\le }$ nazywa się macierzą przejścia od bazy $e_1,...,e_n$ do bazy $e'_1,...,e'_n$. Macierz przejścia jest macierzą izomorfizmu przestrzeni $V$, który przekształca bazę $e_1,...,e_n$ na bazę $e'_1,...,e'_n$ i macierz ta jest utworzona przy bazie $e_1,...,e_n$. W szczególności, macierz przejścia jest macierzą odwracalną.

Zamieńmy rolami dane bazy. Istnieją jednoznacznie wyznaczone skalary $q_{ij}$, $1\le i,j\le n$, takie, że

Macierz $[q_{ij}]$ oznaczmy przez $Q$.

Otrzymujemy więc następujące równości

dla każdego $i=1,...,n$. Oznacza to, że $\displaystyle \sum _{j=1}^n p_{lj}q_{ji}=\delta _{li}$ i, w konsekwencji, macierze $P$ i $Q$ są wzajemnie odwrotne.

Niech teraz $f:V\longrightarrow V$ będzie odwzorowaniem liniowym. Niech $A$ będzie macierzą tego odwzorowania przy bazie $e_1,...,e_n$ i $B$ będzie macierzą tego samego odwzorowania $f$ przy bazie $e'_1,...,e'_n$. Chcemy ustalić związek między macierzami $A$ i $B$.

Mamy następujące równości

Z drugiej strony

Otrzymaliśmy równość $AP=PB$. A zatem udowodniliśmy następujące twierdzenie

Twierdzenie 4.1

Jeżeli $A$ jest macierzą endomorfizmu $f$ przy bazie $e_1,..., e_n$ i $B$ jest macierzą tego samego endomorfizmu przy bazie $e'_1,..., e'_n$, to

gdzie $P$ jest macierzą przejścia od bazy $e_1,...,e_n$ do bazy $e'_1,...,e'_n$.