Formy kwadratowe | Informatyka MIMUW

Niech \(V\) będzie przestrzenią wektorową nad ciałem o charakterystyce różnej od 2. Odwzorowanie

\(f:V\longrightarrow {\mathbb K}\)

nazywamy formą kwadratową, jeśli istnieje odwzorowanie dwuliniowe

\(\Phi : V^2\longrightarrow {\mathbb K}\)

takie, że

\(\Phi (v,v)=f(v)\)

dla każdego \(v\in V\). Mówimy, że odwzorowanie dwuliniowe \(\Phi\) indukuje formę kwadratową \(f\).

Udowodnimy najpierw następujący lemat

Lemat 0.1

Dla formy kwadratowej \(f:V\longrightarrow {\mathbb K}\) istnieje dokładnie jedno odwzorowanie dwuliniowe symetryczne \(\phi : V^2\longrightarrow {\mathbb K}\) indukujące \(f\).

Dowód

Niech \(\Phi\) będzie pewnym odwzorowaniem dwuliniowym indukującym \(f\). Zdefiniujmy odwzorowanie \(\phi\) następująco

\(\phi (u,v)= (1+1)^{-1}\left (\Phi (u,v) +\Phi (v,u)\right ).\)

Odwzorowanie to jest dwuliniowe, symetryczne i indukuje \(f\). Zauważmy, że tutaj właśnie wykorzystaliśmy założenie, że charakterystyka ciała \({\mathbb K}\) jest różna od \(2\).

Jedyność symetrycznego \(\phi\) indukującego \(f\) wykazujemy jak następuje.

Niech \(\phi '\), \(\phi ''\) będą odwzorowaniami dwuliniowymi symetrycznymi indukującymi \(f\). Wtedy \(\phi =\phi '-\phi ''\) jest odwzorowaniem dwuliniowym symetrycznym takim, że \(\phi (v,v)=0\) dla każdego \(v\in V\). Wykorzystując dwuliniowość i symetrię \(\phi\) otrzymujemy następujące równości

\(0=\phi (u+v, u+v)=\phi (u,u)+ 2\phi (u,v) +\phi (v,v)=2\phi (u,v)\)

dla dowolnych wektorów \(u,v\in V\). A zatem \(\phi ' (u,v)=\phi ''(u,v)\) dla dowolnych \(u,v\in V\).

Jedyne dwuliniowe odwzorowanie symetryczne indukujące \(f\) nazywa się odwzorowaniem dwuliniowym skojarzonym z formą kwadratową \(f\).

Dla odwzorowania dwuliniowego \(\Phi\) rozważamy odwzorowanie

\(\tilde \Phi:V\ni v\longrightarrow \{ V\ni u\longrightarrow \Phi (u,v)\in {\mathbb K}\}\in V^*.\) (0.1)

Odwzorowanie to jest oczywiście liniowe.

Od tego momentu zakładamy, że wszystkie rozważane w tym wykładzie przestrzenie są skończenie wymiarowe.

Macierz odwzorowania dwuliniowego

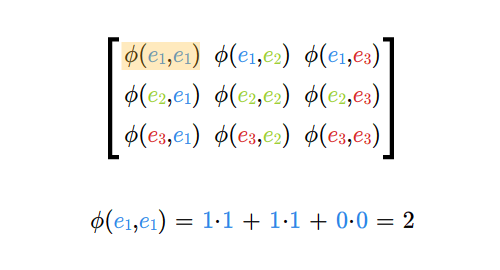
Niech \(e_1,...e_n\) będzie bazą przestrzeni \(V\) zaś \(e^*_1,...,e^*_n\) będzie jej bazą dualną. Znajdźmy macierz odwzorowania \(\tilde \Phi\) przy tak wybranych baz. Skorzystajmy ze wzoru (5.4) z Wykładu IV.

Otrzymujemy następujące równości

\(\begin{aligned} \tilde \Phi (e_j)&= (\tilde\Phi (e_j))(e_1)e^*_1+...+(\tilde \Phi (e_j))(e_n)e^*_n\\ &= \Phi (e_j, e_1)e^*_1+...+\Phi (e_j, e_n)e^*_n. \end{aligned}\)

Oznacza to, że poszukiwana macierz \(\tilde \Phi\) jest równa macierzy \([\Phi (e_i, e_j)]\). Macierz tę nazywamy macierzą odwzorowania dwuliniowego w bazie \(e_1,...,e_n\).

Jeżeli \(\phi\) jest odwzorowaniem dwuliniowym skojarzonym z formą kwadratową \(f\), to macierz tę nazywa się macierzą formy kwadratowej \(f\) przy bazie \(e_1,...,e_n\). Macierz formy kwadratowej jest symetryczna. Rząd tej macierzy jest rzędem odwzorowania liniowego \(\tilde\phi\) i nazywa się rzędem formy kwadratowej \(f\).

Mając bazę \(e_1,...,e_n\) przestrzeni \(V\) i macierz formy kwadratowej \(f\) możemy znaleźć wartość \(f\) na dowolnym wektorze \(v\in V\). Mianowicie, jeśli \(\phi\) jest odwzorowaniem dwuliniowym skojarzonym z \(f\), \(a_{ij}=\phi(e_i,e_j)\) oraz \(v=v_1e_1+...+e_ne_n\), to

\(\displaystyle f(v)=\sum _{i,j=1}^n v_iv_ja_{ij}.\) (0.2)

Zobaczmy jeszcze, jak zmienia się macierz odwzorowania dwuliniowego, jeśli zmienimy bazę. Niech więc dane będą dwie bazy przestrzeni wektorowej \(V\): \(e_1,...,e_n\), \(e'_1,...e'_n\). Niech \(P\) będzie macierzą przejścia od bazy \(e_1,...,e_n\) do bazy \(e'_1,...,e'_n\), tzn.

\(\displaystyle e'_j=\sum _{i=1}^k p_{ij} e_i,\)

dla \(j=1,...,n\) (porównaj rozdział 4. Wykładu VI). Jeśli \(\Phi :V\times V\longrightarrow {\mathbb K}\) jest odwzorowaniem dwuliniowym, to zachodzą następujące równości

\(\displaystyle \Phi (e'_i, e'_j)= \Phi \left (\sum _{k=1}^n p_{ki}e_k, \sum _{l=1}^n p_{lj}e_l\right )= \sum _{k,l=1}^n p_{ki}\Phi (e_k,e_l) p_{lj}.\)

A zatem przy zmianie bazy macierz odwzorowania dwuliniowego zmienia się według wzoru

\(A'= P^* A P,\) (0.3)

gdzie \(A\) jest macierzą \(\Phi\) przy bazie \(e_1,...,e_n\), zaś \(A'\) jest macierzą \(\Phi\) przy bazie \(e'_1,...,e'_n\).

Co prawda udowodniliśmy już, że rząd macierzy \(\Phi\) nie zależy od wyboru bazy, ale warto zauważyć, że wynika to również z powyższego wzoru, bo \(P\) jest macierzą nieosobliwą.

Formy kwadratowe w przestrzeni nad ciałem \({\mathbb R}\)

Celem tego rozdziału jest pokazanie, że w przestrzeni wektorowej nad ciałem \({\mathbb R}\), każda forma kwadratowa ma macierz szczególnie prostej postaci.

Rozważymy najpierw formy kwadratowe w przestrzeniach euklidesowych. Udowodnimy teraz twierdzenie Lagrange'a

Twierdzenie 1.1

Niech \(f\) będzie formą kwadratową na skończenie wymiarowej przestrzeni euklidesowej \(V\). Istnieje baza ortonormalna \(e_1,...,e_n\) przestrzeni \(V\), przy której macierz \(A\) formy kwadratowej \(f\) jest diagonalna i \(a_{11}\ge...\ge a_{nn}\), gdzie \(a_{11},...,a_{nn}\) są wyrazami głównej przekątnej macierzy \(A\).

Dowód

Dowód twierdzenia jest indukcyjny ze względu na wymiar przestrzeni \(V\).

Dla \(n=1\) twierdzenie jest trywialne. Załóżmy, że jest prawdziwe dla \((n-1)\).

Niech \(f\) będzie formą kwadratową na \(n\)-wymiarowej przestrzeni euklidesowej \(V\). W przestrzeni \(V\) mamy naturalną topologię. Albo wprowadzimy ją przez normę (którą mamy, bo iloczyn skalarny definiuje normę), albo bierzemy dowolny izomorfizm liniowy \(h: V\longrightarrow {\mathbb R} ^n\) i mówimy, że podzbiór \(C\) przestrzeni \(V\) jest otwarty wtedy i tylko wtedy, gdy \(h(C)\) jest otwarty w \({\mathbb R} ^n\). Ponieważ każde odwzorowanie liniowe przestrzeni \({\mathbb R} ^n\) jest ciągłe, więc tak zdefiniowana topologia nie zależy od wyboru izomorfizmu \(h\). Tak czy inaczej, sfera jednostkowa

\(S^{n-1}= \{ v\in V |\ \ \Vert v\Vert =1\}\)

jest zbiorem zwartym a forma kwadratowa jest odwzorowaniem ciągłym na \(V\) (porównaj wzór (0.2)).

A zatem istnieje wektor \(e_1\in S ^{n-1}\), w którym funkcja \(f\) osiąga swoje maksimum. Niech \(W\) będzie dopełnieniem ortogonalnym do podprzestrzeni \({\rm lin} \{e_1\}\). Podprzestrzeń \(W\) jest \((n-1)\)-wymiarowa.

Na podstawie założenia indukcyjnego wiemy, że dla \(\tilde f=f_{|W}\) istnieje baza ortonormalna \(e_2,...,e_n\) przestrzeni \(W\), przy której macierz \(\tilde f\) jest diagonalna i wyrazy na głównej przekątnej tworzą ciąg niemalejący. Twierdzimy, że \(e_1,...,e_n\) jest bazą \(V\) spełniającą żądane warunki.

Po pierwsze \(e_1,...e_n\) jest oczywiście bazą ortonormalną \(V\) i \(\phi (e_1,e_1)=f(e_1) \ge f(e_i)= \phi (e_i,e_i)\) dla każdego \(i=2,...n\), bo wszystkie \(e_2,...,e_n\) należą do \(S ^{n-1}\). Wystarczy teraz pokazać, że \(\phi (e_1,e_i)=0\) dla każdego \(i=2,...n\). W tym celu, dla ustalonego wskaźnika \(i=2,...,n\), rozważmy funkcję

\(F:{\mathbb R}\ni \tau \longrightarrow f((\cos \tau )\, e_1 +(\sin\tau )\, e_i)\in {\mathbb R} .\)

Wektor \((\cos \tau )\, e_1 +(\sin\tau )\, e_i\) należy do \(S ^{n-1}\) dla każdego \(\tau\). Ponieważ \(f\) osiąga w \(e_1\) maksimum, więc funkcja \(F\) osiąga maksimum w \(\tau =0\). Zatem \(F'(0)=0\). Mamy następujące równości

\(F(\tau )=(\cos ^2 \tau ) \phi (e_1,e_1) +(\sin ^2\tau )\phi (e_i,e_i) +{1\over 2} \sin (2\tau )\phi (e_1, e_i).\)

Łatwo stad wyliczyć, że

\(F'(0) = \phi (e_1, e_i).\)

Wobec tego \(\phi (e_1, e_i)=0\), co kończy dowód twierdzenia.

Udowodnimy teraz twierdzenie o bezwładności form kwadratowych, zwane także twierdzeniem Sylvestera.

Twierdzenie 1.2 [Sylvestera]

Niech \(V\) będzie \(n\)-wymiarową przestrzenią wektorową nad ciałem \({\mathbb R}\). Dla każdej formy kwadratowej \(f\) na \(V\) istnieje baza \(e_1,...,e_n\), przy której macierz \(f\) jest postaci blokowej

\(\left [\begin{array} {lcr} \ {\rm I} _p \ \ 0\ \ \ 0\\ \ 0\ {-{\rm I}} _q \ \ 0\\ \ 0\ \ \ 0\ \ \ 0 \end{array} \right ],\)

gdzie \({\rm I} _k\) jest macierzą jednostkową o wymiarach \(k\) na \(k\).

Liczby \(p\) i \(q\) nie zależą od wyboru bazy \(e_1,...,e_n\).

Dowód

Na przestrzeni wektorowej \(V\) wprowadzamy dowolny iloczyn skalarny (porównaj Przykład 1.4 z Wykładu X) Z twierdzenia Lagrange'a wiemy, że istnieje baza ortonormalna, przy której macierz formy \(f\) jest taka, jak to opisano w poprzednim twierdzeniu. Uporządkujmy tę bazę tak, aby na głównej przekątnej najpierw (tzn. począwszy od lewego górnego rogu) pojawiły się wyrazy dodatnie, potem ujemne i na końcu wyrazy zerowe. Wystarczy teraz pomnożyć wektory bazy odpowiadające niezerowym wyrazom macierzy pomnożyć przez przez odpowiedni skalar. Jeśli \(\phi (e_i,e_i) = a_{ii}\ne 0\), to \(e_i\) zastępujemy wektorem \({1\over {\sqrt {|a_{ii}|}}}e_i.\)

Udowodnimy teraz druga część twierdzenia. Widać, że \(p+q\) jest rzędem formy kwadratowej \(f\), a zatem nie zależy od wyboru bazy. Załóżmy, że dla dwóch baz \(e_1,...,e_n\) i \(e'_1,...e'_n\) spełniających tezę twierdzenia mamy pary liczb \(p, q\) oraz \(p',q'\) odpowiednio. Wiemy, że \(p+q=p'+q'\). Wystarczy więc pokazać, że \(p=p'\).

Dla dowodu nie wprost przypuśćmy, że \(p'>p\). Niech \(U\) będzie podprzestrzenią wektorową generowaną przez wektory \(e_{p+1},...,e_n\), zaś \(W\) - podprzestrzenią generowaną przez wektory \(e'_1,...,e'_{p'}\). Mamy następujący ciąg równości i nierówności

\(\begin{aligned} n=dim V&\ge \dim (U+W)\\ &= \dim U +\dim W-\dim (U\cap W)\\ &= (n-p) +p' -\dim (U\cap W). \end{aligned}\)

Wobec tego \(\dim (U\cap W)\ge p'-p>0\). Istnieje więc wektor \(0\ne v\in (U\cap W)\). Niech \(v=v_1e_1+...+v_ne_n\) i \(v=v'_1e'_1+...+v'_ne'_n\). Ponieważ \(v\in U\), więc

\(f(v)=-(v_{p+1})^2-...-(v_{p+q})^2\le 0.\)

Ponieważ \(v\in W\), więc

\(f(v)=(v'_1)^2+...+(v'_{p'})^2\ge 0.\)

Porównując te nierowności widzimy, że \(f(v)=0\). Ponieważ \(v\in U\), więc \(v=v_{p+1}e_{p+1}+...+v_{p+q}e_{p+q}\). Korzystając z tego, że \(0=f(v)=-(v_{p+1})^2-...-(v_{p+q})^2\), otrzymujemy, że \(v=0\), co jest sprzeczne z naszym założeniem. Dowód twierdzenia jest zakończony.

Z twierdzenia Sylvestera wynika, że przy pewnej bazie \(e_1,...,e_n\) forma kwadratowa dana jest w postaci kanonicznej, tj. wyraża się wzorem

\(f(v)=(v_1)^2+...+(v_p)^2-(v_{p+1})^2-...-(v_{p+q})^2,\) (1.4)

dla \(\displaystyle v=\sum _{i=1}^nv_ie_i\).

Definicja 1.3 [Sygnatura]

Parę liczb \((p,q)\) nazywamy sygnaturą formy kwadratowej.

Mówimy, że forma kwadratowa \(f\) jest półokreślona dodatnio, jeśli w powyższym przedstawieniu (1.4) są same plusy. Jeśli są same plusy i \(p=n=\dim V\), to mówimy, że forma kwadratowa jest dodatnio określona. Podobnie definiuje się formy półokreślone ujemnie i określone ujemnie. Forma kwadratowa nazywa się formą określoną, jeśli jest określona dodatnio lub ujemnie.

Niech \(f:V\longrightarrow V\) będzie endomorfizmem. Mówimy, że odwzorowanie \(f\) jest symetryczne, jeśli

\(f(v)\cdot w= f(w)\cdot v\)

dla każdych wektorów \(v,w\in V\).

Niech \(\phi\) będzie odwzorowaniem dwuliniowym (symetrycznym) zdefiniowanym formułą

\(\phi (v,w)=f(v)\cdot w.\)

Odwzorowanie to jest odwzorowaniem skojarzonym pewnej formy kwadratowej. Ze wzoru (1.4) z Wykładu XI i z twierdzenia Lagrange'a wynika, że istnieje baza ortonormalna, przy której macierz odwzorowania \(f\) jest diagonalna. Jest to bardzo szczególny przypadek endomorfizmu mającego bardzo prostą macierz Jordana.