Problem
Przygotujmy teraz arkusz, w którym wystąpią proste formuły. Jako pierwszy przykład wykonajmy proste zestawienie wydatków. W tym celu sporządzimy tabelę z trzema kolumnami. W poszczególnych wierszach tej tabeli zapiszemy informacje o kolejnych operacjach finansowych. I tak w pierwszej kolumnie będziemy zapisywać wykonaną transakcję, przy czym wydatki będziemy wpisywać ze znakiem minus, a przychody ze znakiem plus. W drugiej kolumnie wpiszemy aktualne saldo, czyli stan naszych finansów po wykonaniu operacji. Trzecia kolumna posłuży jako komentarz dotyczący danej operacji. Pierwszy wiersz tabeli będzie niepełny: nie będzie opisywał żadnej operacji, a jedynie zawierał informacje o początkowych saldzie. A oto przykład takiego zestawienia:
Spróbuj samodzielnie przygotować sobie taką tabelkę, nie wpisując do niej na razie żadnych danych liczbowych ani formuł, a jedynie nadając jej kształt graficzny używając poleceń do formatowania omówionych w poprzednim module. Należy przy tym wykonać następujące czynności:
- Przygotować nagłówek:
- scalić komórki A5, B5, C5
- do scalonej komórki wpisać tytuł zestawienia
- zwiększyć rozmiar czcionki i ustawić jest wytłuszczenie
- wycentrować tekst w komórce
- Przygotować nagłówki poszczególnych kolumn:
- wpisać tytuły nagłówków do komórek A7, B7, C7
- zaznaczyć zakres A7:C7 i ustawić rozmiar czcionki, centrowanie tekstu i wytłuszczenie
- Ustawić kolory tła w poszczególnych kolumnach poprzez:
- zaznaczenie odpowiednich zakresów
- zmianę koloru tła
- Zaznaczyć zakres A7:C16 i włączyć wyświetlanie wszystkich krawędzi
- Ustawić format danych w komórkach A8:B16 na waluta
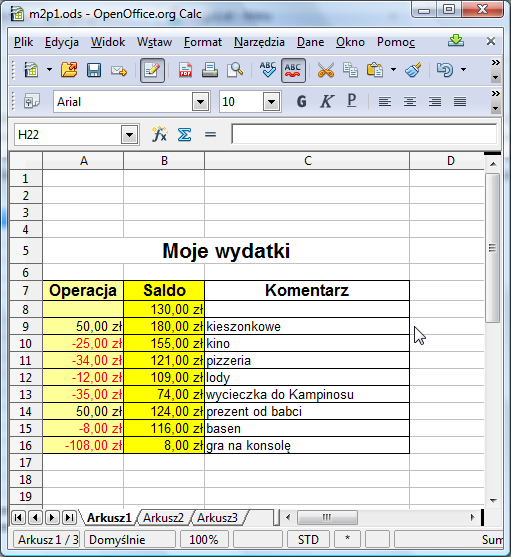
Poprawne wykonanie powyższych czynności powinno doprowadzić do uzyskania poniższej tabeli.
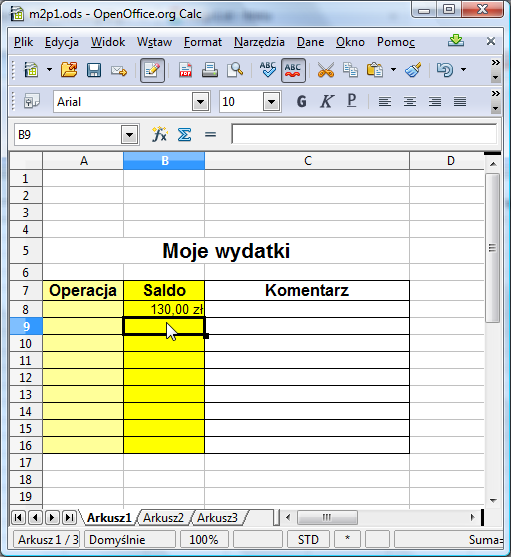
Do komórki B8 wpisz teraz kwotę, jaką dysponujesz początkowo, na przykład 130. Wpisz samą liczbę 130, nie wpisuj słowa zł ani pln. Jeśli format danych został ustawiony poprawnie, to nazwa waluty powinna pojawić się automatyczne.
Wprowadzanie formuł
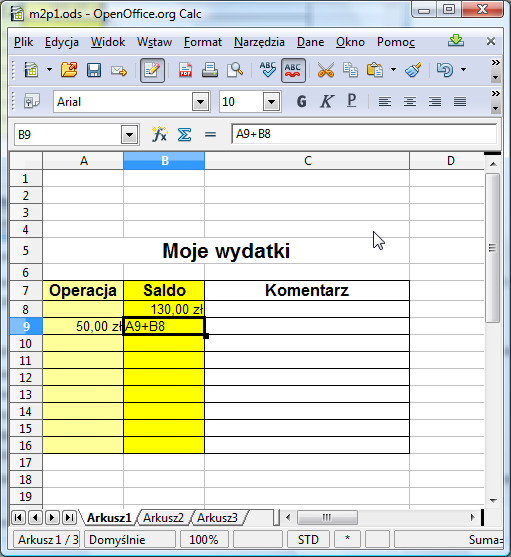
Wprowadźmy teraz pierwszą operację. Przypuśćmy, że Twoje konto zasiliło kieszonkowe od rodziców w wysokości 50 zł. Wpisujemy zatem do komórki A9 liczbę 50. Pamiętaj! Tak jak poprzednio nie wpisuj nazwy waluty! W przeciwnym razie arkusz kalkulacyjny zinterpretuje wprowadzoną wartość jako tekst i komórka A9 nie będzie mogła być argumentem operacji arytmetycznych.
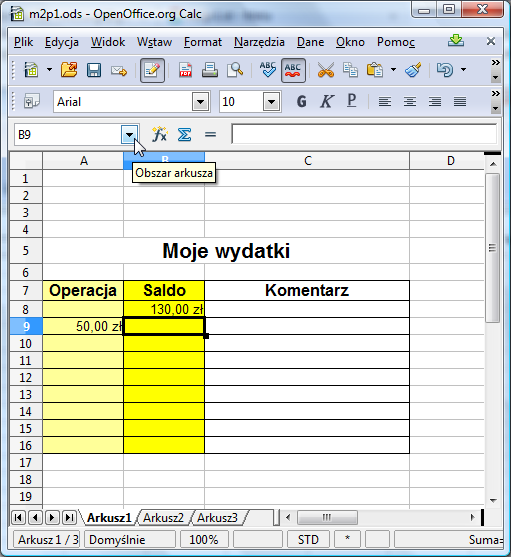
Posiadasz teraz 130 zł + 50 zł = 180 zł. Jak zmusić arkusz kalkulacyjny do automatycznego wykonania tego wyliczenia? Sprawa jest prosta: trzeba wpisać w odpowiednie miejsce właściwą formułę. Chcemy, aby w komórce B9 znalazło się aktualne saldo. Aktualne saldo wylicza się dodając do poprzedniego salda (znajdującego się w komórce B8) kwotę aktualnej operacji (zapisaną w komórce A9). Ustawiamy się więc w komórce B9 i wpisujemy do niej formułę: =A9+B8:
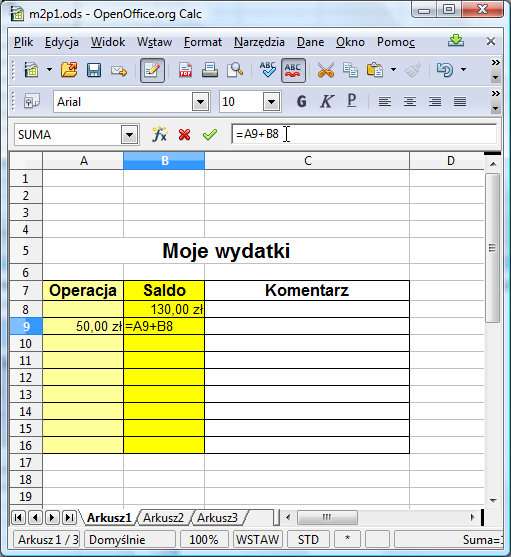
Następnie zatwierdzamy ją wciskając klawisz Enter.Jeśli wszystko przebiegło pomyślnie, to w polu B9 zobaczymy wyliczoną wartość 130+50, czyli 180. Zauważ, że wartość ta jest wyliczona, nie wprowadzona. Jeśli klikniesz na pole B9, to w polu edycji nie zobaczysz wartości 180, lecz wprowadzoną właśnie formułę.
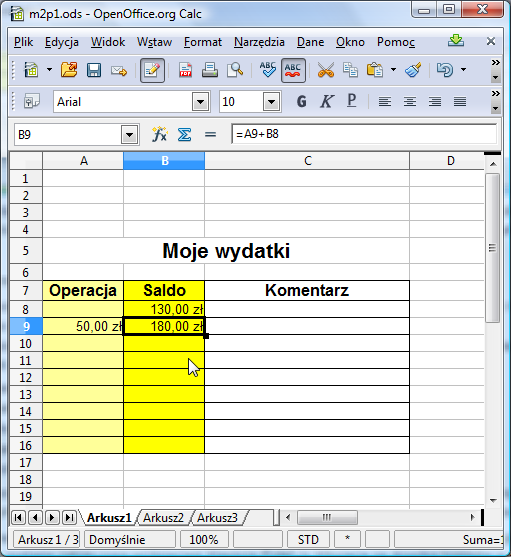
Wprowadzając formuły warto pamiętać o następujących ważnych faktach:
- Formuła musi zaczynać się od znaku =. Wpisujemy =A9+B8, a nie A9+B8. Jeśli pominiemy znak równości, to arkusz zinterpretuje wprowadzone znaki jako napis i w komórce pojawi się po prostu napis A9+B8, jak w przykładzie poniżej:
- Zamiast wpisywać adresy komórek można w trakcie edytowania formuły kliknąć myszką w odpowiednie komórki. Zamiast więc wpisywać =A9+B8 możemy postąpić tak:
- Ustawiamy się w B9 i wpisujemy znak równości.
- Klikamy na A9 i sprawdzamy, czy w polu edycji pojawił się adres A9.
- Wpisujemy znak +.
- Klikamy na B8 i sprawdzamy, czy w polu edycji pojawił się adres B8.
- Wciskamy klawisz Enter.
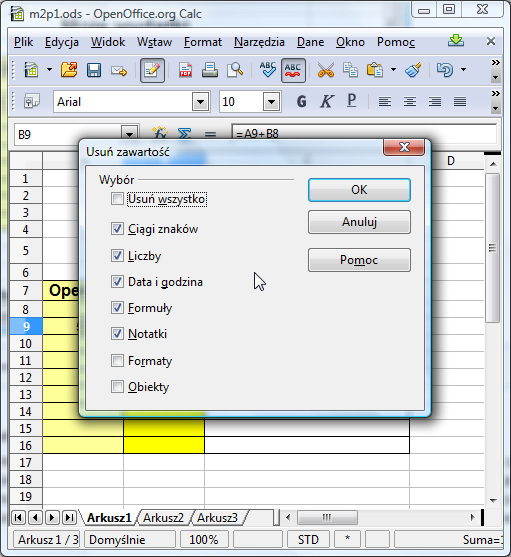
Wypróbuj ten sposób. Kliknij najpierw prawym klawiszem myszy na komórkę B9 i z menu podręcznego wybierz opcję Usuń zawartość:
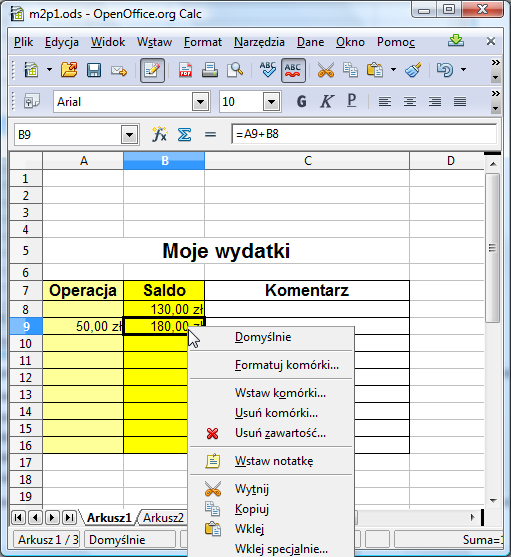
Potwierdź swój zamiar w okienku dialogowym wciskając OK. Jeśli chcesz zachować formatowanie upewnij się przedtem, że pola Formaty i Usuń wszystko są odznaczone :
Następnie wprowadź jeszcze raz powyższą formułę stosując tym razem opisany powyżej sposób.
Choć powyższa metoda wprowadzania formuł stanowi pewne ułatwienie, to jednak sprawia ona problemy początkującym użytkownikom arkusza. Chodzi o to, że dopóki edycja formuły nie zostanie zakończona wciśnięciem klawisza Enter, to kliknięcie na dowolną komórkę w arkuszu wstawia jej adres w miejsce kursora w polu edycji. A czasem zdarza się zapomnieć o zatwierdzeniu formuły klawiszem Enter. Przekonaj się sam, jakie kłopoty mogą się wówczas pojawić. Wyczyść jeszcze raz zawartość komórki B9, wprowadź ponownie formułę klikając na odpowiednie komórki arkusza, ale nie naciskaj Enter. Kliknij teraz w jakieś inne miejsce arkusza i zobacz, co się stało!
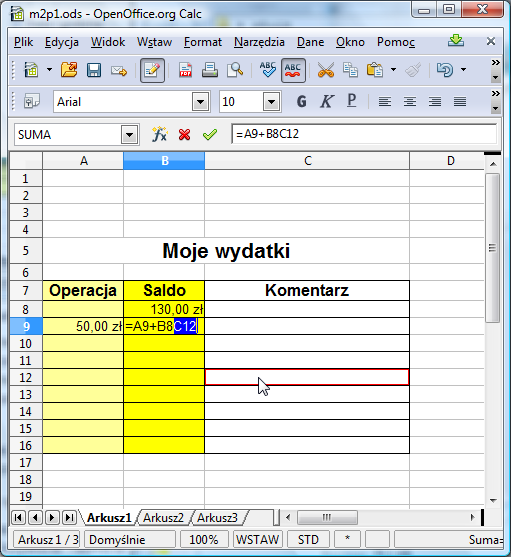
Oczywiście sytuacja jest do opanowania: można przecież usunąć niepotrzebne elementy formuły klawiszem Backspace. Zapamiętaj jednak ten efekt i nie daj się w przyszłości zaskoczyć arkuszowi!
Adresowanie względne
Wprowadźmy teraz w wierszu 10 kolejną operację. Przypuśćmy, że wydałeś 25 zł na kino. Do komórki A10 wpisz zatem wartość -25, a do komórki B10 odpowiednią formułę. Jaka to będzie formuła? Oczywiście: =A10+B9. Po jej wpisaniu (i zatwierdzeniu klawiszem Enter - pamiętasz?) w B10 pojawi się aktualne saldo.
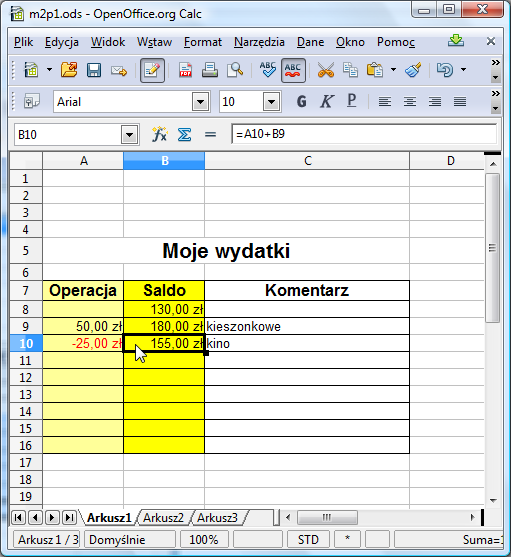
Zauważmy, że formuła =A10+B9 wpisywana do komórki B10 jest w istocie bardzo podobna do formuły =A9+B8 wpisywanej do komórki B9. Obie formuły opisują tak naprawdę tę samą czynność: dodaj zawartość komórki znajdującej się w tej samej kolumnie w poprzednim wierszu do komórki znajdującej się w tym samym wierszu w poprzedniej kolumnie. Gdy wpisujemy formułę do B10, komórką w tej samej kolumnie, ale w poprzednim wierszu jest B9, a komórką w tym samym wierszu i poprzedniej kolumnie jest A10. Podobnie, gdy wpisujemy formułę do B9, komórką w tej samej kolumnie, ale w poprzednim wierszu jest B8, a komórką w tym samym wierszu i poprzedniej kolumnie jest A9. Taki sposób adresowania: wyrażenie adresu pewnej komórki (na przykład B9) względem innej komórki (na przykład B10) nosi nazwę adresu względnego. Arkusz kalkulacyjny zapamiętuje adresy komórek występujących w formule właśnie w taki względny sposób, przy czym komórką odniesienia jest zawsze ta komórka, do której jest wpisany adres.
- Ćwiczenie
- Spróbuj samodzielnie wyrazić słowami w języku polskim sens formuły =B1*C3 znajdującej się w komórce D2. Gwiazdka oznacza mnożenie.
Ponieważ arkusz pamięta adresy w sposób względne, a przy adresowaniu względnym formuły spod adresów B9 i B10 są tymi samymi formułami, więc zamiast wpisywać formułę do B10 można po prostu skopiować do niej komórkę B9. Przekonaj się sam, że ten sposób działa. Wyczyść najpierw zawartość komórki B10, a następnie skopiuj zawartość komórki B9 (klikając na niej prawym klawiszem myszy i wybierając z menu podręcznego opcję Kopiuj) i wklej ją do B10 (prawy klawisz myszy na B10 i Wklej).
Przeciąganie
Opisany powyżej scenariusz jest bardzo częsty w arkuszu kalkulacyjnym. Często wręcz projektujemy arkusz w taki sposób, aby wszystkie formuły w pewnych kolumnach lub pewnych wierszach były wyliczane za pomocą tej samej formuły. Tak też jest w naszym przykładzie. W kolumnie B tabeli powinny znaleźć się identyczne formuły: dodaj zawartość komórki znajdującej się w tej samej kolumnie w poprzednim wierszu do komórki znajdującej się w tym samym wierszu w poprzedniej kolumnie. Wygodnie byłoby więc wpisać taką formułę do jednej komórki, na przykład do B9 (już to zrobiliśmy uprzednio), a następnie skopiować ją do wielu komórek znajdujących się w tej samej kolumnie. Ponieważ taka konieczność pojawia się bardzo często, arkusz kalkulacyjny oferuje specjalną metodę kopiowania do wielu komórek. Technika, o której mowa, nazywa się przeciąganiem.
Spróbujmy teraz "przeciągnąć" zawartość komórki B9 do komórek B10:B16. Klikamy na komórkę B9. Zauważmy, że wokół B9 pojawia się ramka, a w jej prawym dolnym rogu widać mały kwadrat:
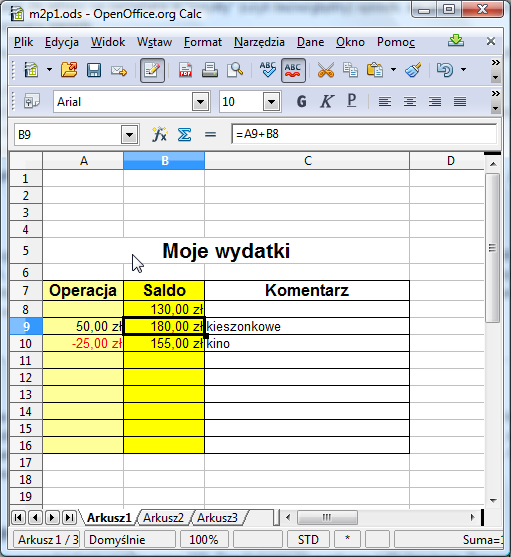
Gdy ustawimy wskaźnik myszy na tym kwadraciku, kursor zmieni kształt na krzyżyk. Teraz wystarczy wcisnąć lewy klawisz myszy i trzymając go wciśnięty przesunąć ją w dół tak, aby ramka objęła komórki B10:B16.
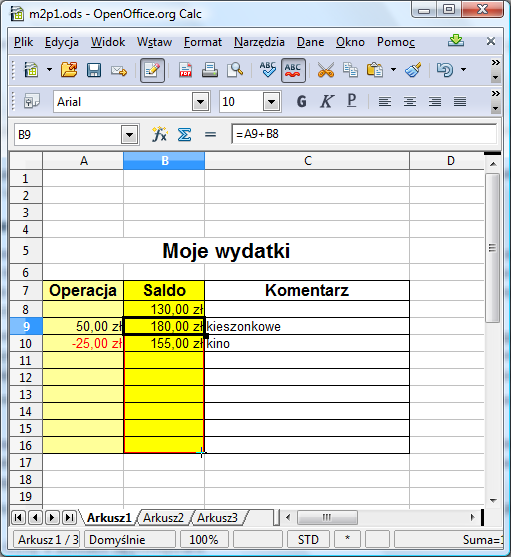
Jeśli wszystko przebiegło pomyślnie, to po puszczeniu klawisza myszy, aktualna wartość salda powinna powielić się na wskazany zakres komórek. Jednak po wpisaniu wartości w komórki A9:A16, wartości w kolumnie B zmienią się uwzględniając aktualny stan konta.
Zapamiętaj dobrze technikę przeciągania! Jest to jedna z podstawowych metod tworzenia zestawień w arkuszu kalkulacyjnym. Wiedząc, jak działa adresowanie względne i przeciąganie można projektować zestawienia i później szybko obliczać w nich potrzebne dane.
Adresowanie względne i przeciąganie - inne spojrzenie
Podejrzyjmy teraz formuły, które powstały na skutek właśnie wykonanego przeciągnięcia komórki B9 w dół. Przypomnijmy, że w B9 znajdowała się formuła =A9+B8. Zajrzyjmy do komórki B10. W tym celu klikamy na nią. Następnie przechodzimy do trybu edycji klikając myszką w polu edycji. W polu edycji widzimy formułę =A10+B9. Dodatkowo komórki występujące w tej formule są zaznaczone w arkuszu za pomocą ramek odpowiednich kolorów.
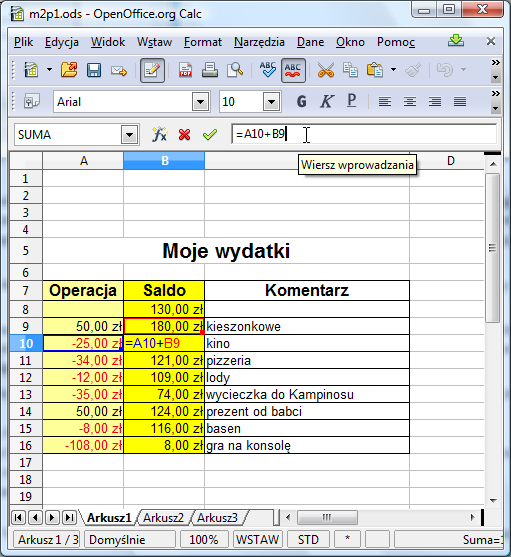
Gdy zajrzymy do B11 (pamiętaliście o zakończeniu edycji klawiszem Enter? Jeśli nie, to teraz trzeba wyjść z edycji anulując zmiany dokonane w sposób niezamierzony - wciskając klawisz Esc), zobaczymy =A11+B10.
Analizując adresy komórek występujące w formułach powstałych przez przeciąganie możemy zauważyć następującą prawidłowość. Gdy przeciągamy formułę w dół, to liczbowa część adresu komórek występujących w tej formule jest zwiększana. Z B8 w naszym przykładzie zrobiło się B9, B10 itd. Łatwo sprawdzić, że przy przeciąganiu w górę, liczby w adresach maleją. Analogicznie przeciąganie w prawo powoduje "zwiększanie" literowej części adresu (z B robi się C, D itd), a przeciąganie w lewo "zmniejsza" litery w adresie.
- Ćwiczenie
- Wykonaj eksperyment z przeciąganiem. W tym celu do komórki G10 wpisz formułę =F11. Przeciągaj następnie komórkę G10 w różne strony obserwując, co dzieje się z adresem F11.
Powyższe obserwacje umożliwiają nieco inne spojrzenie na sposób pamiętania przez arkusz adresów komórek. Zamiast wyobrażać sobie, że adresy komórek występujących w formule są pamiętane w sposób względny, możemy wyobrażać sobie, że adresy są pamiętane w "zwykły" (czyli bezwzględny) sposób, ale przeciągnięcie lub skopiowanie formuły powoduje zmianę wszystkich adresów w niej występujących w następujący sposób:
- Jeśli przeciągamy formułę w dół, to wszystkie liczby w adresach są zwiększane. Na przykład, jeśli formułę =B7+C4 przeciągniemy jedną pozycję w dół, to zmieni się ona na =B8+C5.
- Jeśli formuła jest przeciągana w górę, to wszystkie liczby w adresach są zmniejszane.
- Jeśli formuła jest przeciągana w lewo, to wszystkie litery w adresach są "zmniejszane" (tzn. Z zmienia się na Y, Y na X, ..., B na A). Na przykład, jeśli formułę =B7+C4 przeciągniemy jedną pozycję w lewo, to zmieni się ona na =A7+B4
- Jeśli formuła jest przeciągana w prawo, to wszystkie litery w adresach są "zwiększane".
- Ćwiczenie
- Jaka formuła znajdzie się w D12, jeśli przeciągniemy 10 wierszy w dół formułę =B1*C3 znajdującą się w komórce D2? Co będzie w I2, jeśli formułę z D2 przeciągniemy 5 pozycji w prawo?
Propozycje ćwiczeń
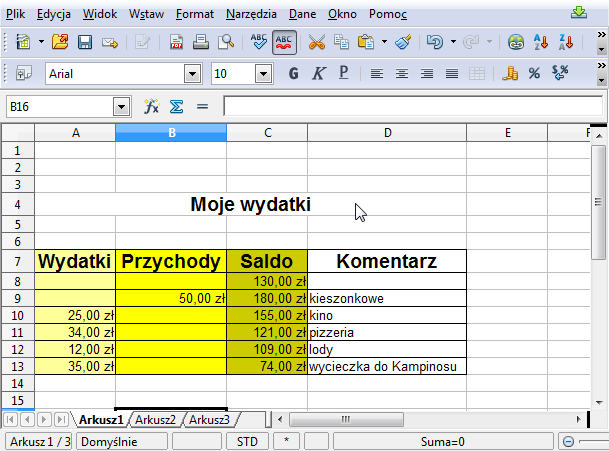
Spróbuj nieco zmodyfikować opracowany arkusz kalkulacyjny. Oddzielmy teraz wydatki od wpływów. Przygotuj arkusz przedstawiający Twój budżet w postaci tabeli z czterema kolumnami. Wydatki będziemy umieszczać w kolumnie A, przychody w kolumnie B, aktualne saldo będzie wyliczane w kolumnie C, a kolumnę D wykorzystamy do opisu operacji. W dalszym ciągu zakładamy, że w każdym wierszu opisujemy tylko jedną operację, przy czym jeśli jest to wydatek, to (dodatnią) kwotę umieszczamy w kolumnie A, a jeśli przychód do (dodatnią kwotę) umieszczamy w kolumnie B. W każdym wierszu jedna z kolumn A lub B jest pusta. Oto przykład takiego zestawienia.
Proste przykłady formuł z procentami
Przypomnienie pojęcia procenta
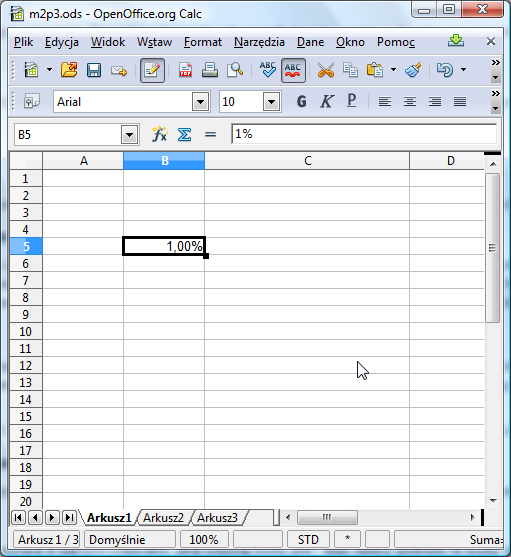
Przed wykonaniem kolejnych ćwiczeń przypomnijmy sobie pojęcie procenta. Przygotuj sobie pusty arkusz kalkulacyjny i wpisz w dowolną jego komórkę wyrażenie 1%. Zwróć uwagę, aby znak procenta nie został pominięty! Zatwierdź dane klawiszem Enter. Być może w komórce arkusza zobaczysz 1,00% - arkusz domyślnie wyświetla liczby z dwiema cyframi po przecinku:
Zmień teraz sposób formatowania tej komórki. W tym celu kliknij prawym klawiszem myszy w komórkę i wybierz opcję Formatuj komórki:
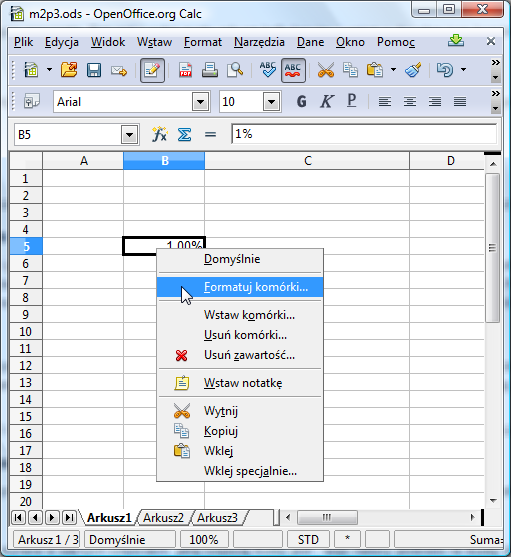
W dialogu, który się pojawi wybierz zakładkę Liczby i zmień Kategorię z Procent na Liczba.
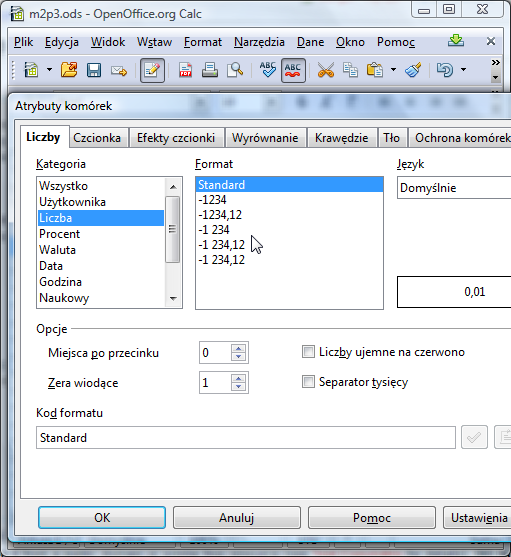
Zauważ, że 1,00% zamieniło się na 0,01.
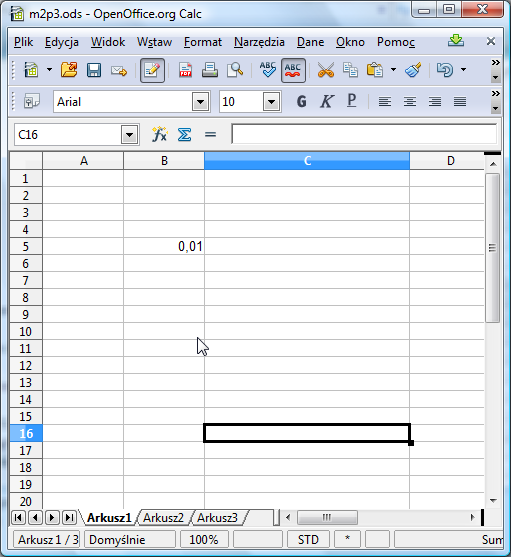
Faktycznie, 1% to po prostu jedna setna pewnej całości. 1% liczby 1234, to jedna setna liczby 1234 czyli 12,34. 10% z 50 to dziesięć setnych z 50 czyli jedna dziesiąta liczby 50 czyli 5.
Jak obliczać procenty w arkuszu kalkulacyjnym
Obliczenie x% z liczby y, to wykonanie zwykłego mnożenia xy i podzielenie wyniku przez 100. Przećwiczmy to w arkuszu kalkulacyjnym. Przygotuj sobie arkusz przedstawiony poniżej. Zwróć przy tym uwagę, aby wartości liczbowe były wpisane w osobnych komórkach i aby poza tymi liczbami nic w tych komórkach nie było. Zadbaj o formatowanie. Być może trzeba będzie wyłączyć wyświetlanie cyfr po przecinku w A6 i C6.
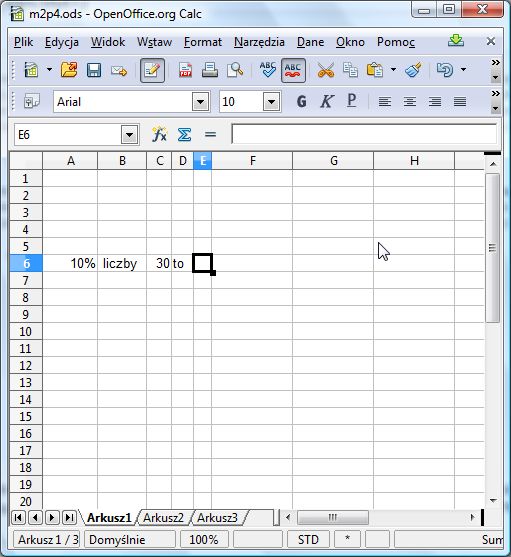
Czy wiesz już jaką formułę należy wpisać do komórki E6? Oczywiście: =A6*C6. Przypomnijmy, że mnożenie wyraża się za pomocą gwiazdki. A dlaczego nie jest potrzebne dzielenie przez 100? Przypomnij sobie poprzedni eksperyment. Po wpisaniu do komórki wartości 1% i zmianie sposobu jej formatowania, arkusz interpretował ją jako 0,01 - zatem dzielenie przez 100 było uwzględnione już tutaj.
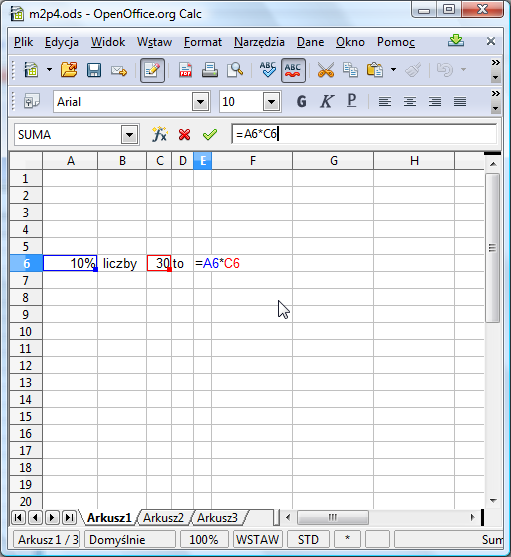
Poeksperymentuj z arkuszem zmieniając wartości w polach A6 i C6. Zauważ, że po każdej zmianie, wartość w komórce E6 jest automatycznie przeliczana.
Rozwiązania typowych zadań na procenty za pomocą arkusza kalkulacyjnego
Spróbujmy rozwiązać teraz kilka typowych zadań, w których występuje pojęcie procenta. Zacznijmy od zadania "odwrotnego" do poprzedniego przykładu.
Jakim procentem liczby x jest y?
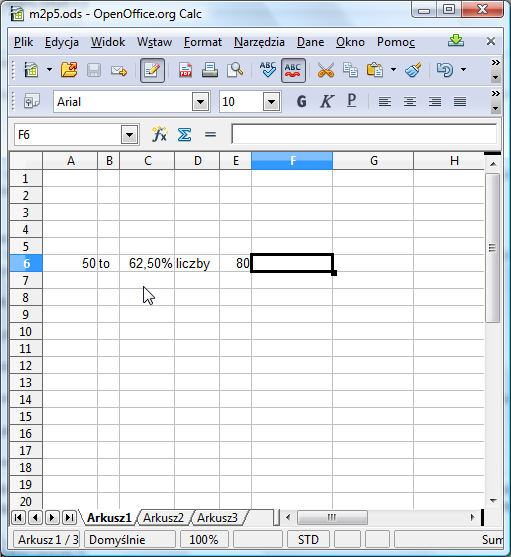
Jaką formułę należy wpisać do komórki C6? Ponieważ procent wyraża w setnych częściach, jaką częścią liczby E6 jest A6, więc należy podzielić A6 przez E6. Dzielenie zapisuje się za pomocą znaku /:
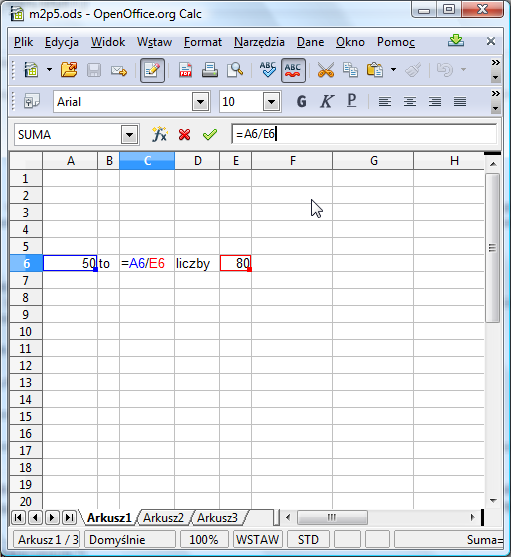
Pole C6 trzeba jednak sformatować tak, aby wyświetlało wartość w procentach (Formatuj komórki z menu podręcznego, następnie zakładka Liczby, kategoria Procent).
O ile procent x jest większe od y, a o ile y jest mniejsze od x
Kolejny przykład jest nieco bardziej złożony. Do przedstawionego poniżej arkusza chcemy wpisywać dwie liczby: większą w pole zaznaczone na żółte, mniejszą - w pole zaznaczone na zielono. Arkusz powinien sam wypełnić wartościami pozostałe pola liczbowe, czyli C6, A7, C7 i E7.
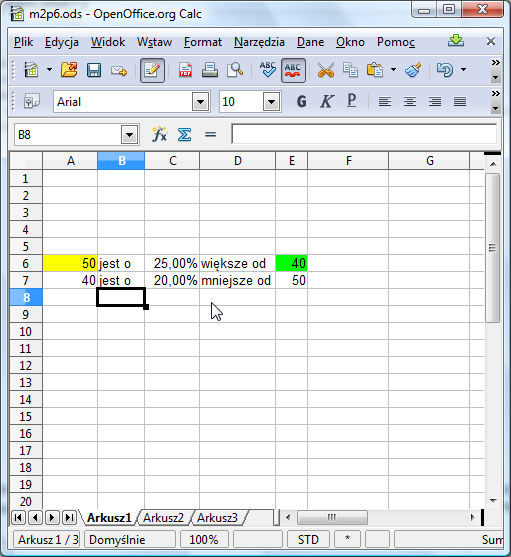
Zacznijmy od komórek A7 i E7. W A7 ma się pojawić dokładnie to, co w E6, a w E7 - to co w A6. Odpowiednimi formułami są zatem:
- =E6 w komórce A7
- =A6 w komórce E7
Jakie formuły należy jednak wpisać do C6 i C7? Gdyby formuła w komórce C6 miała określać po prostu o ile A6 jest większe od E6, to byłaby po prostu różnicą =A6-E6. My jednak pytamy, o ile procent te komórki się różnią. Zatem różnicę należy odnieść do liczby, z którą porównujemy A6, czyli do E6. Zatem odpowiedzią jest iloraz A6-E6 i E6, co w arkuszu opisujemy formułą =(A6-E6)/E6:
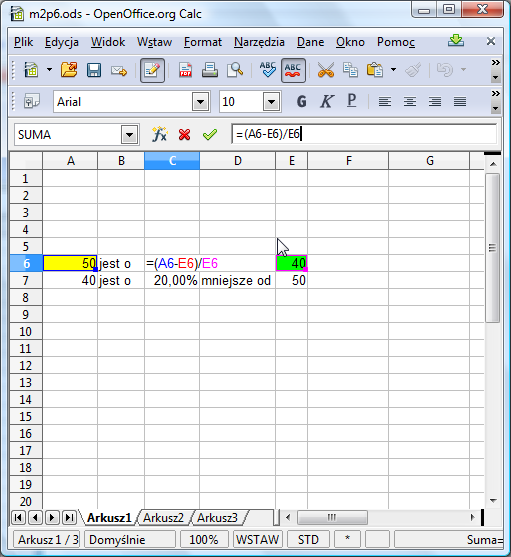
Nawiasy są niezbędne do zapewnienia właściwej kolejności obliczeń.
- Ćwiczenie
- Jaką formułę wpiszesz do C7?
- Ćwiczenie
- Poeksperymentuj z tym arkuszem. Zmieniaj wartości w A6 i E6 i obserwuj, jak zmieniają się wartości w pozostałych polach.
Pewną liczbę zwiększono o x%, a potem zmniejszono o x%. O ile procent w efekcie zmniejszono tę liczbę?
Przeanalizujmy teraz następujący arkusz:
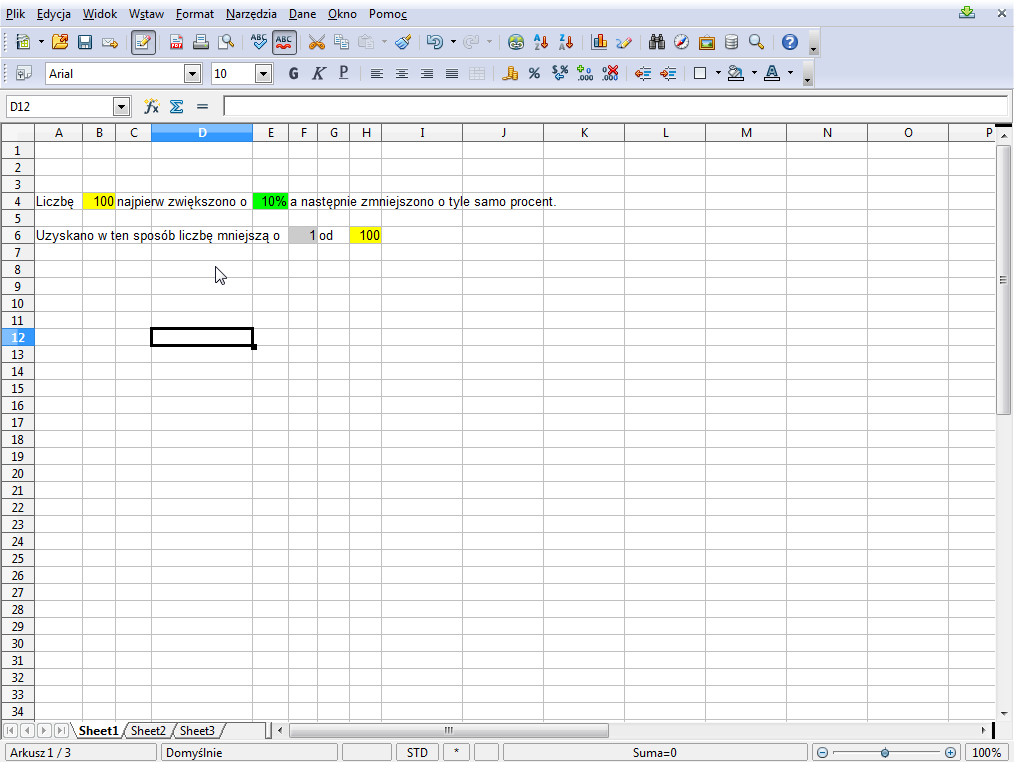
Chcemy wpisywać dane w pole B4 oraz E4. Arkusz powinien sam skopiować do H6 wartość z pola B4 oraz policzyć wartość w polu F6.
- Ćwiczenie
- Jaką formułę wpisać do H6?
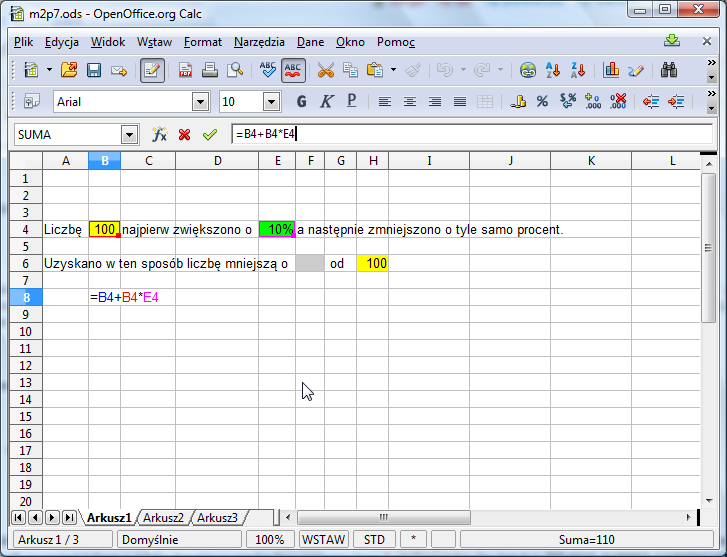
Zadanie rozwiążemy przeprowadzając obliczenia pomocnicze. Najpierw w komórce B8 obliczymy, jaka jest wartość pierwotnej liczby po zwiększeniu jej o wskazaną liczbę procent. Liczbę z komórki B4 musimy zwiększyć o (czyli dodać do niej) E4 procent z niej samej, czyli o E4*B4. Zatem właściwa formuła do wpisania w B8 to: =B4+B4*E4 (albo = B$*(1+E4)).
W analogiczny sposób wyznaczymy w komórce C8 wartość o E4 procent mniejszą od B8. Właściwa formuła to =B9-B9*E4
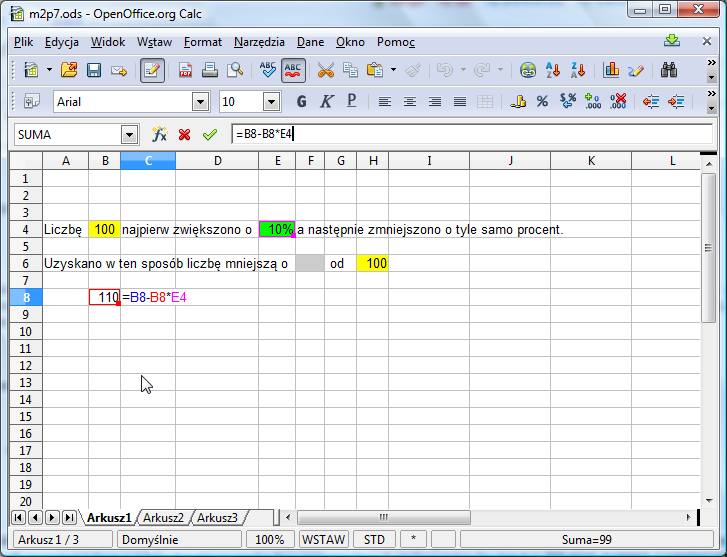
Teraz wystarczy już w pole F6 wpisać szukaną wartość: =(B4-C8)/C8:
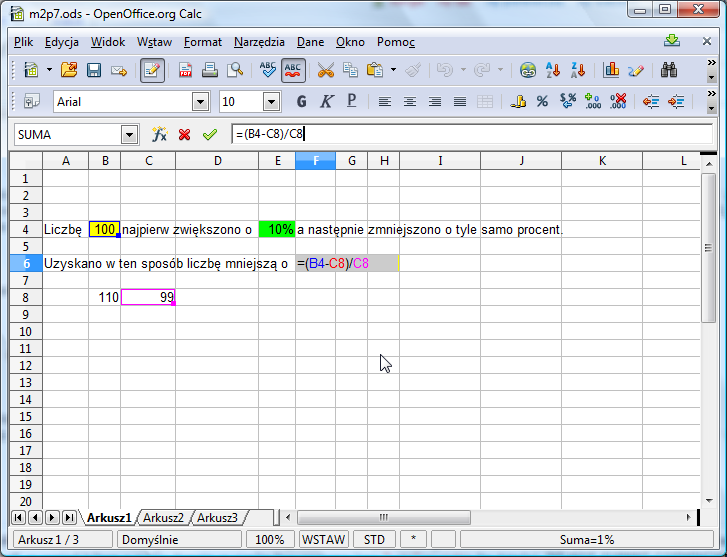
Spróbuj zmienić teraz pierwotną liczbę w komórce B4. Zauważ, że wynik w szarym polu nie zmienił się. Poeksperymentuj z innymi wartościami - w dalszym ciągu nic się nie zmienia. Faktycznie jest bowiem tak, że procentowa zmiana wartości pierwotnej liczby nie zależy od jej wartości.
- Ćwiczenie
- Spróbuj udowodnić powyższą tezę.