Różne sposoby adresowania. Symulacja spłaty kredytu. Tabliczka mnożenia.

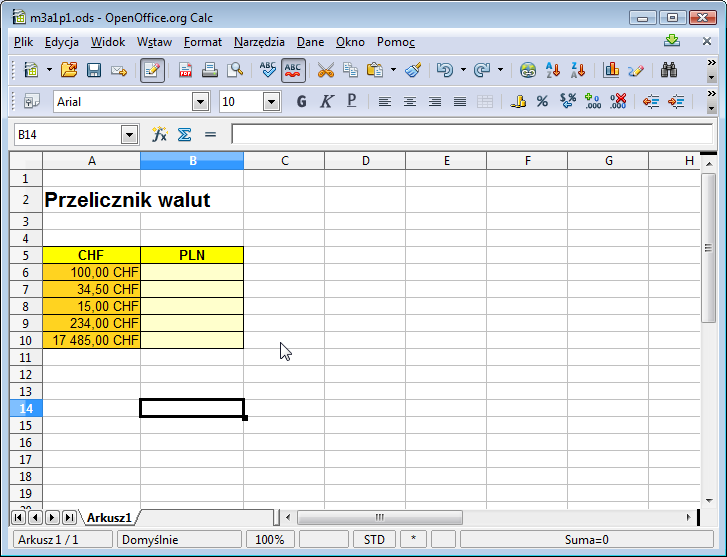
Przygotujmy teraz prosty arkusz, który posłuży nam do przeliczania różnych kwot w jednej walucie na drugą po aktualnym kursie. Dla ustalenia uwagi przyjmijmy, że przeliczamy franki szwajcarskie na złotówki. Przygotujmy za pomocą arkusza kalkulacyjnego tabelę. W jej pierwszej kolumnie wpiszmy kwoty we frankach szwajcarskich, które chcemy przeliczyć na złotówki. Wyniki znajdą się w drugiej kolumnie, którą na razie zostawmy pustą.

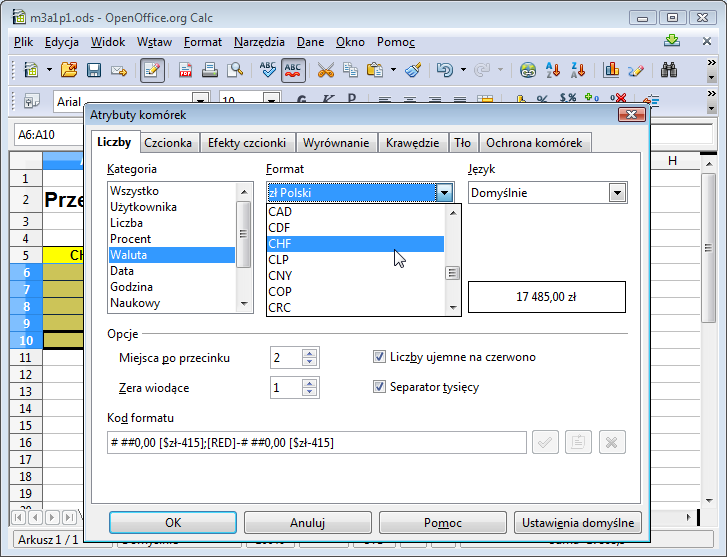
Zwróć uwagę, na formatowanie kolumny pierwszej. Symbol waluty (CHF) nie jest częścią składową pola, ale został wygenerowany automatycznie. Taki efekt jest możliwy do uzyskania tak, jak w przypadku zł w poprzednim module: z menu podręcznego wybieramy Formatuj komórki, a następnie z zakładki Liczby kategorię Waluta. Teraz na rozwijanej liście Format trzeba znaleźć oznaczenie franka szwajcarskiego:

Przeliczanie walut. Metoda pierwsza

Przypuśćmy, że aktualny kurs franka szwajcarskiego wynosi 2,81 zł.

Ćwiczenie

Wpisz do komórki B6 odpowiednią formułę i przeciągnij ją do komórek B7:B10.

Otrzymaliśmy następujący arkusz:

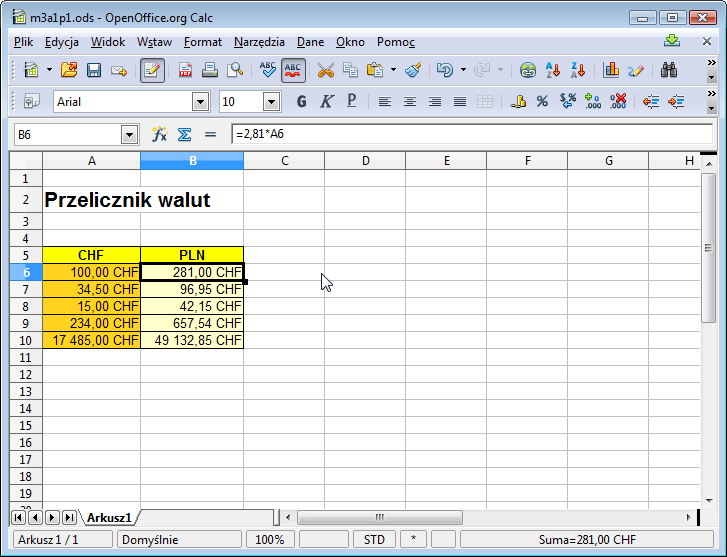
Zauważmy, że opisany w poprzednim module mechanizm adresowania względnego znów dobrze sprawdził się w tym przypadku. Co jednak trzeba zrobić, gdy kurs franka zmieni się? Niestety jest wówczas niezbędna zmiana formuły i ponowne jej przeciągnięcie do wszystkich komórek kolumny B tabeli. Nie jest to wygodne rozwiązanie. Tobie nie sprawi to już wprawdzie większych trudności, ale wyobraź sobie, że arkusz został przygotowany dla osoby, która nie wie nic o formułach!

Przeliczanie walut. Próba usprawnienia

Jak rozwiązać ten problem? Spróbujmy wpisać aktualny kurs do arkusza i odwołać się do niego w formule z komórki B6. Można to zrobić na przykład tak. Jak zwykle w E4 znajduje się jedynie liczba, a symbol waluty uzyskuje się przez odpowiednie formatowanie:

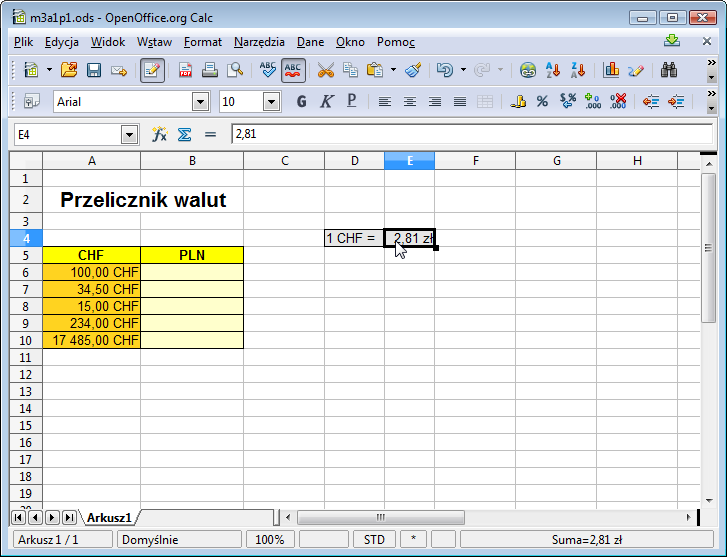
Poprawmy teraz formułę w B6 zastępując stałą 2,81 odwołaniem do odpowiedniej komórki - w tym wypadku będzie to E4.

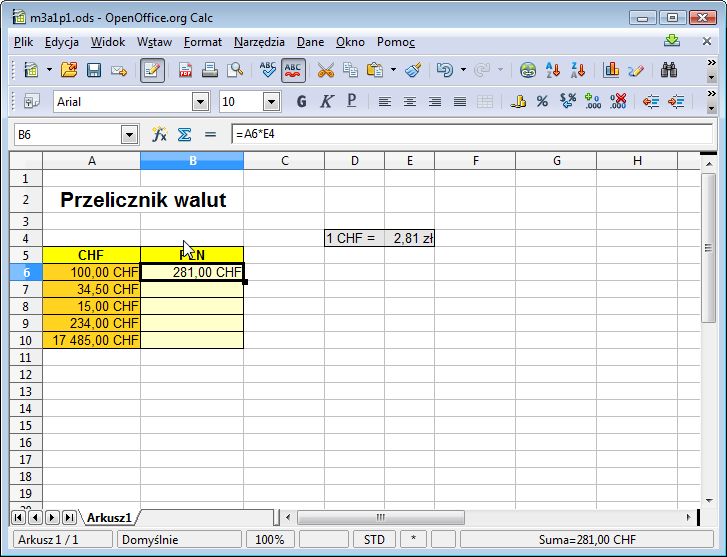
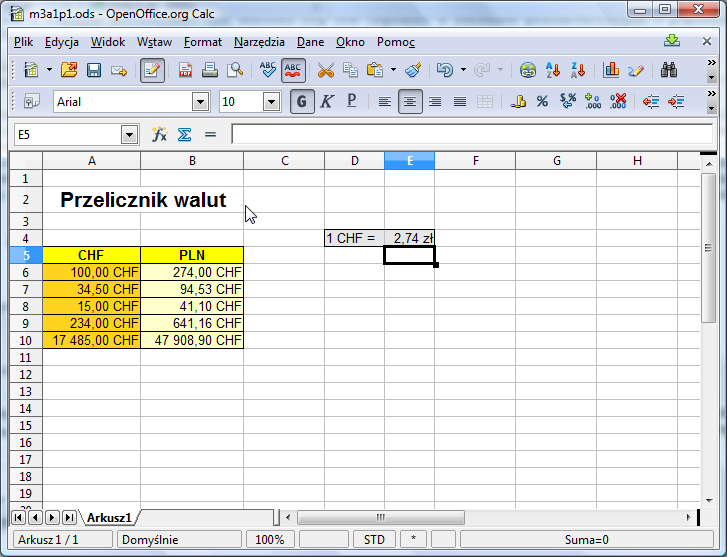
Sprawdzamy wynik w B6 - zgadza się, powinno być 281 zł i faktycznie tak jest. Teraz pozostaje jedynie przeciągnąć formułę z B6 w dół. Wykonujemy to ... i stwierdzamy, że coś się tu nie zgadza wszystkie komórki B7:B10 są równe 0.

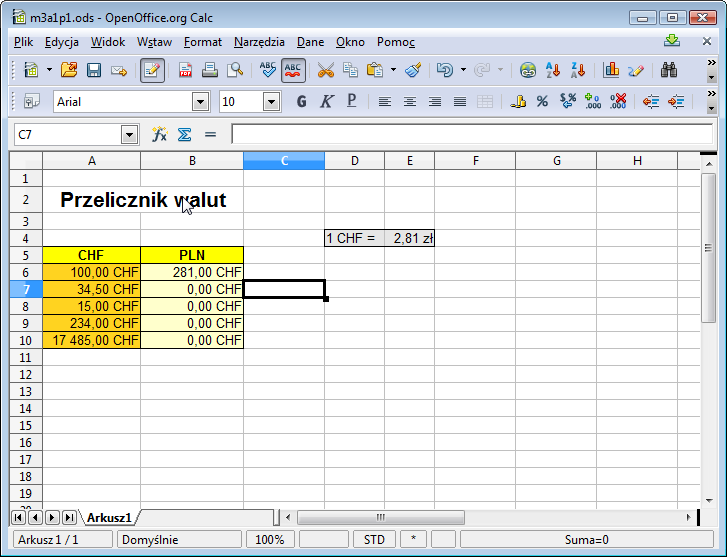
Aby zorientować się, co się stało podejrzyj zawartość komórki B7. No właśnie formuła w B7 to =A7*E5. Adres A6 z oryginalnej formuły zmienił się na A7 i jest to zgodne z naszymi intencjami. Ale zmienił się też (zgodnie z zasadami przedstawionymi w poprzednim module) adres E4 z oryginalnej formuły, a tego w tym wypadku akurat nie chcieliśmy!

Przeliczanie walut. Rozwiązanie poprawne

Przykład ten pokazuje, że domyślny sposób adresowania komórek - adresowanie względne nie zawsze jest odpowiednie w danym zastosowaniu. Na szczęście arkusz kalkulacyjny oferuje także alternatywny sposób adresowania: adresowanie bezwzględne.

Adres komórki, która ma być adresowana w sposób bezwzględny zapisujemy w specyficznej postaci: przed literą oznaczającą kolumnę oraz przed liczbą oznaczającą wiersz wpisujemy znak dolara ($). Jeśli więc chcemy, aby komórka E4 w formule była adresowana bezwzględnie, to zamiast odwoływać się do niej pisząc E4, napiszemy $E$4. Taki sposób wpisania adresu powoduje, że arkusz adresuje komórkę występującą w formule nie względem komórki zawierającej tej adres, lecz zapamiętując jej położenie w obrębie arkusza, na przykład czwarty wiersz, piąta komórka. Taki sposób interpretacji adresu powoduje, że pozostaje on niezmienny przy kopiowaniu formuły do innej komórki. Innymi słowy znaki dolarów w adresie "blokują" przeliczanie adresu przy przeciąganiu lub kopiowaniu formuły.

Możemy teraz poprawić formułę w komórce B6 naszego przykładowego arkusza:

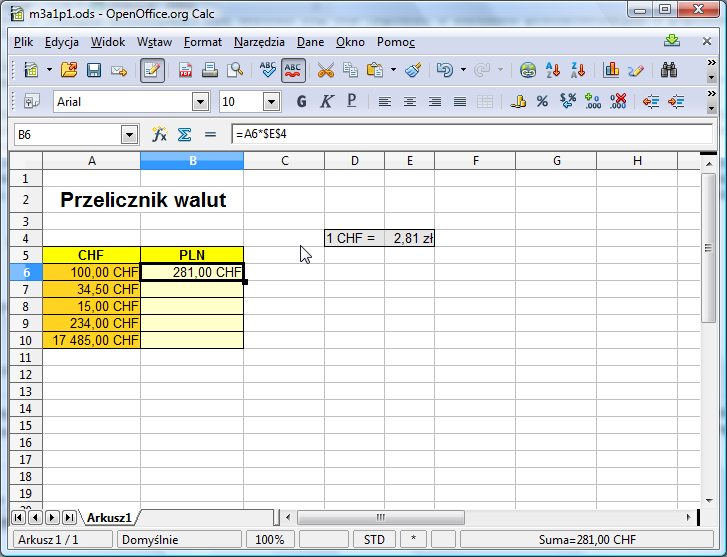
Tym razem po przeciągnięciu formuły z B6 w dół arkusza, wszystkie kwoty przeliczają się poprawnie na złotówki:

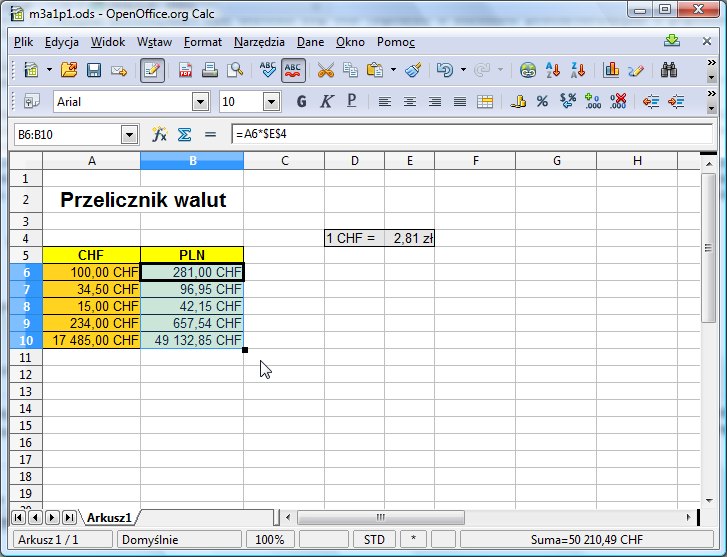
Ponadto zmiana kursu powoduje konieczność wprowadzenia zmiany tylko w jednej komórce: w E4. Cała tabelka przelicza się automatycznie.

Przykłady wykorzystujące różne metody adresowania

Obliczanie stanu lokaty

A oto inny przykład, w którym wykorzystamy adresowanie bezwzględne. Załóżmy, że dysponujesz pewną kwotą pieniędzy. Chcesz je umieścić na lokacie. Znając oprocentowanie lokaty chcesz się dowiedzieć, jaką kwotą będziesz dysponował po roku. Takie obliczenia można bez trudu wykonać w arkuszu kalkulacyjnym:

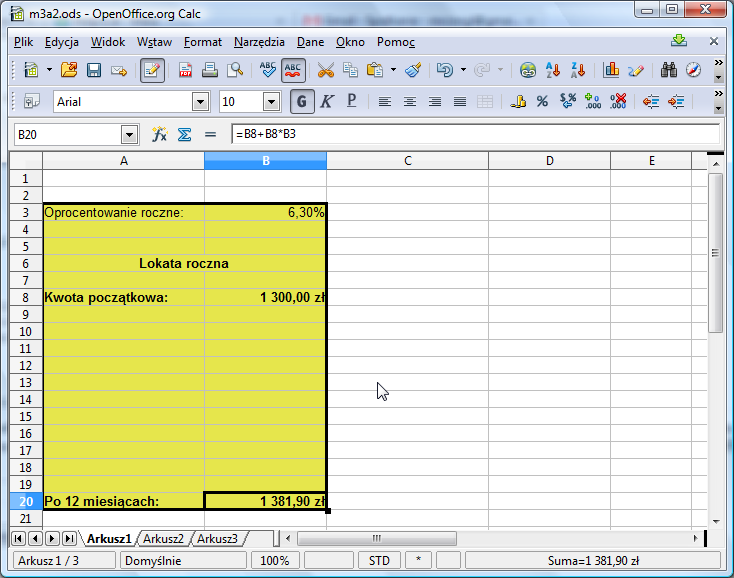
Do komórki B3 wpisujemy oprocentowanie lokaty, do B8 kwotę początkową, a do B20 formułę =B8+B8*B3 obliczającą stan konta po roku. O ile nie planujemy obliczeń stanu lokaty po kolejnych latach adresowanie bezwzględne nie jest tu konieczne, bo nie będziemy przeciągać formuły.

Przypuśćmy teraz, że inny bank oferuje oprocentowanie nieco mniejsze, ale za to lokata jest z miesięczną kapitalizacją odsetek. Znaczy to, że co miesiąc do stanu lokaty są dopisywane odsetki. W kolejnym miesiącu oprocentowanie dotyczy więc nie tylko kwoty początkowej, ale także dopisanych odsetek.

Policzmy, jak będzie wzrastać nasza lokata w poszczególnych miesiącach. Przypuśćmy, że oprocentowanie roczne znajduje się tym razem w komórce D3, a kwota początkowa w komórce D8. Po miesiącu na lokacie będzie kwota wyliczona formułą =D8+D8*$D$3/12. Dzielenie przez 12 jest konieczne, bo D3 jest oprocentowaniem w skali roku, więc oprocentowanie miesięczne wynosi =$D$3/12. Pociągnięcie tej formuły 11 pozycji w dół umożliwi wyliczenie stanu lokaty po 12 miesiącach. Zauważmy, że znaki $ są tym razem niezbędne, gdyż formuła jest kopiowania do kolejnych wierszy:

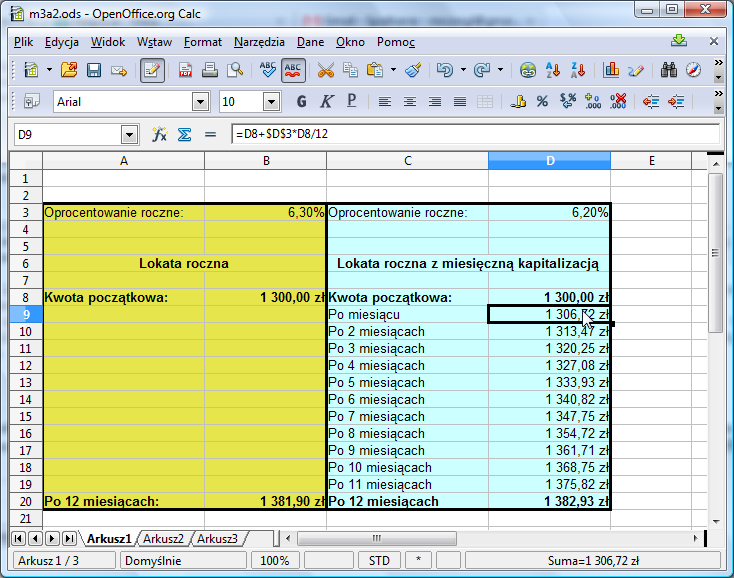
Powyższy przykład pokazuje, że miesięczna kapitalizacja odsetek może rekompensować niewielką różnicę w oprocentowaniu lokaty.

Symulacja spłaty kredytu przy zmiennych ratach

Kolejny przykład jest nieco bardziej złożony. Użyjemy arkusza kalkulacyjnego, żeby obliczyć harmonogram spłat kredytu zaciąganego w banku. Kredyt bierze się na określony czas. My założymy, że jest to kredyt dziesięcioletni, spłacany w 120 miesięcznych ratach. Aby obliczyć wielkość poszczególnych rat musimy znać oprocentowanie kredytu - podaje się go w skali roku oraz kwotę kredytu. Przyjmijmy, że kredyt jest na 150 tysięcy złotych i jest na 8,5% w skali roku. Wpiszmy te "parametry" kredytu w komórki arkusza kalkulacyjnego:

Jak bank oblicza poszczególne raty? Ponieważ musimy spłacić 150 tysięcy złotych w 120 miesięcznych ratach, więc każdego miesiąca musimy spłacić kwotę 150000/120= 1250 zł. Ta wielkość nosi nazwę raty kapitałowej. Wpiszmy do komórki C4 arkusz odpowiednią formułę:

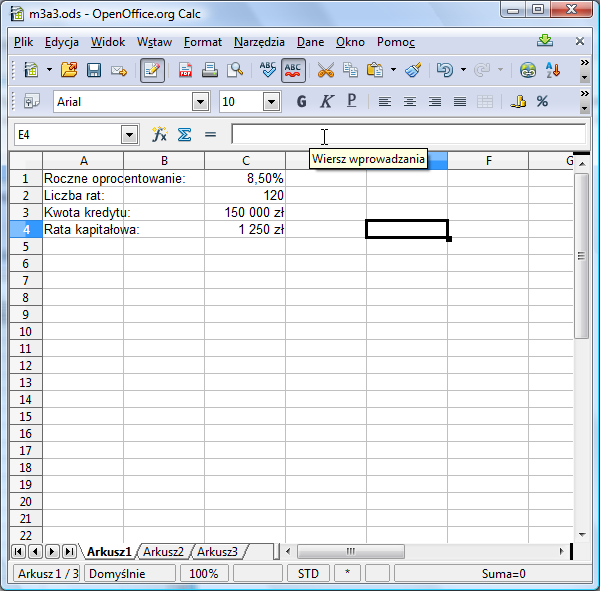
Użyliśmy znaku dolara w celu zaznaczenia adresowania bezwzględnego na wypadek, gdybyśmy musieli skopiować formułę z C4 w inne miejsce arkusza. Jeśli wiadomo, że formuła nie będzie nigdzie kopiowania, to symbole $ można by pominąć. Tak właśnie będzie w tym przypadku, ale dobrą praktyką jest ich pozostawienie na wypadek, gdybyśmy zmienili zdanie i chcieli jednak skopiować tę formułę w inne miejsce arkusza.

Jednak rata kapitałowa to nie wszystko. Każdego miesiąca bank dolicza do niej odsetki od aktualnego zadłużenia. Aktualne zadłużenie to kwota, jaką w danej chwili mamy jeszcze do spłacenia. Pierwszego miesiąca jest to więc cała kwota kredytu (150 tysięcy w naszym przypadku), a każdego kolejnego miesiąca zadłużenie maleje o ratę kapitałową.

Przygotujmy teraz tabelkę, w której policzymy kolejne raty. Tabela będzie składać się z czterech kolumn. W pierwszej wpiszemy numer kolejnej raty, w drugiej będziemy liczyć aktualne zadłużenie, w trzeciej wyliczymy odsetki, które bank doliczy do danej raty, a w czwartej wpiszemy formułę obliczającą wielkość raty.

Wpiszmy i sformatujmy nagłówek tabeli i wypełnijmy dwa pierwsze element w jej pierwszym wierszu: będzie to pierwsza rata, a zadłużenie na początku wynosi tyle, ile wartość kredytu:

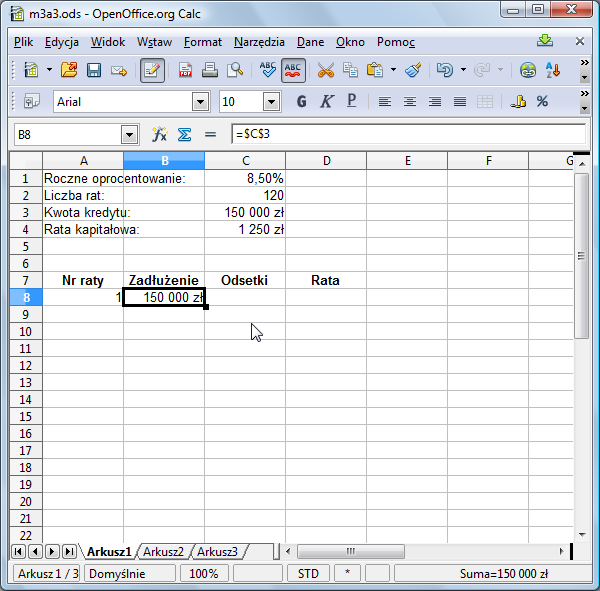
Zwróć uwagę, że w komórce B8 znajduje się formuła (=$C$4), a nie ponownie wpisana kwota kredytu (150 tys). Dzięki temu, chcąc uzyskać wielkość rat przy innej kwocie kredytu wystarczy zmienić wartość w komórce C4.

Ćwiczenie

Odsetki są naliczone od aktualnego zadłużenia, czyli od wartości z kolumny B tabeli. Oprocentowanie jest 1/12 oprocentowania rocznego (wartość z C1). Wpisz odpowiednią formułę do komórki C8. Weź przy tym pod uwagę fakt, że formuła, którą wpiszesz będzie kopiowana (przeciągana) w dół do wszystkich komórek w kolumnie C tabeli. Zadbaj o prawidłowy sposób adresowania!

Prawidłowe rozwiązanie tego ćwiczenia to =B8*$C$1/12. Komórka B8 jest adresowana względnie, bo po skopiowaniu formuły do kolejnego wiersza oprocentowanie ma być liczone od wartości z B9. Komórka $C$1 jest adresowana bezwzględnie, bo we wszystkich kolejnych wierszach wartość oprocentowania ma być brana z C1.

Teraz wpiszmy odpowiednią formułę do komórki D8. Całkowita kwota pierwszej raty jest sumą raty kapitałowej i aktualnych odsetek.

Ćwiczenie

Wpisz odpowiednią formułę.

Jeśli poprawnie wykonałeś ćwiczenie, arkusz powinien wyglądać jak na poniższym rysunku. Sprawdź formułę w D8!

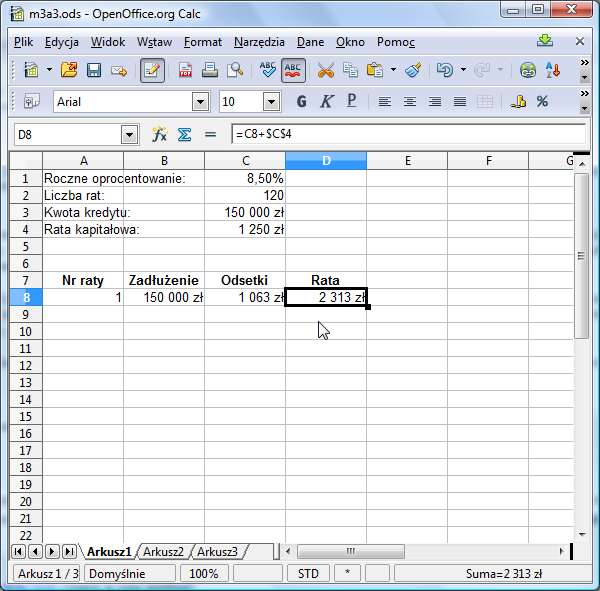
Świetnie! Właśnie wyliczyliśmy pierwszą ratę kredytu. A co z pozostałymi? Wiemy, że będzie ich 120. Zatem w pierwszą kolumnę tworzonej tabeli musimy wpisać kolejne liczby od 1 do 120 - są to numery kolejnych rat. Na szczęście nie musimy pracowicie wpisywać ich jedna po drugiej. Skorzystamy z ... przeciągania! Przeciągnięcie w dół komórki, w której znajduje się liczba, powoduje wpisywanie do kolejnych komórek ciągu następujących po sobie liczb całkowitych. Skorzystajmy z tej techniki. Chwytamy myszką za kwadrat w prawym dolnym rogu A8 i ciągniemy 120 komórek w dół:

Teraz czas na komórkę B9. Wpiszemy formułę wyliczającą aktualne zadłużenie. Przypomnijmy: od zadłużenia w poprzednim miesiącu trzeba odjąć ratę kapitałową. Odpowiednia formuła to =B8-$C$4. Ciągniemy 120 komórek w dół i powinniśmy otrzymać ciąg liczb, z których każda kolejna jest mniejsza od poprzedniej o 1250 zł.

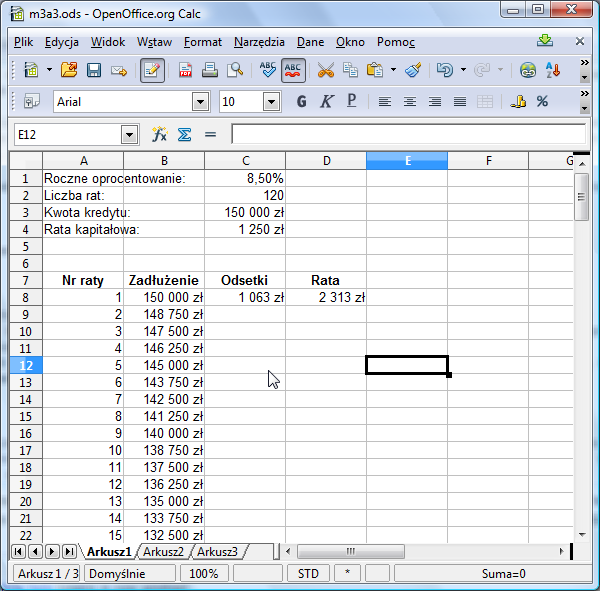
Aby policzyć odsetki w kolejnych ratach trzeba pociągnąć w dół formułę z C8. Przeciągnięcie formuły z D8 spowoduje wyliczenie wartości kolejnych rat. Zerknijmy na koniec tabeli:

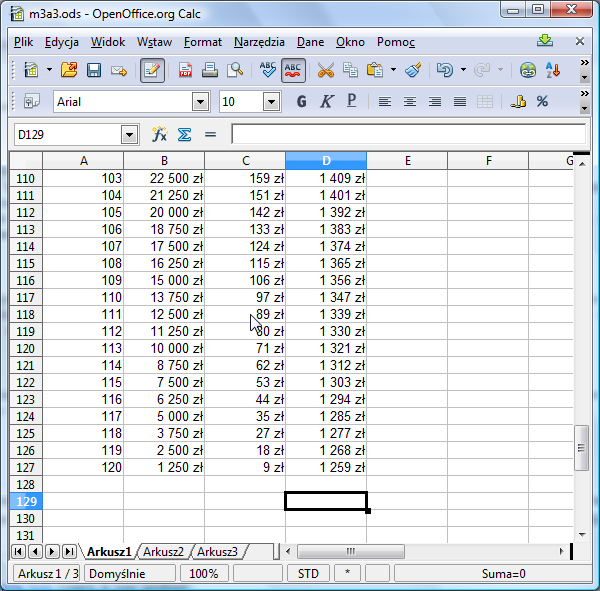
Widzimy, że ostatnia rata wynosi 1259 zł podczas gdy pierwsza wynosiła 2313 zł.

Sumowanie wielu komórek

Przypuśćmy, że chcemy teraz dowiedzieć się, ile łącznie pieniędzy wpłacimy do banku. W tym celu trzeba zsumować wszystkie wartości z kolumny D począwszy od D8 na D127 skończywszy. W praktyce bardzo często zachodzi konieczność sumowania całych kolumn lub wierszy liczb. Z tego powodu do arkusza wprowadzono wygodne narzędzie do sumowania.

Przypuśćmy, że w komórce D129 chcemy wyliczyć sumę wszystkich rat. Ustaw się więc w komórce D129, a następnie kliknij znak sigma znajdujący się obok pola edycji:

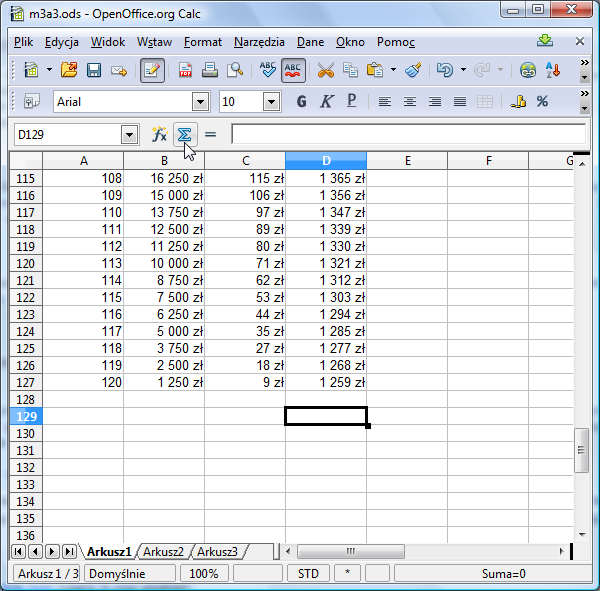
Znak ten oznacza sumowanie wielu wartości. Arkusz próbuje zgadnąć, w jakim obszarze znajdują się liczby do zsumowania. W naszym przypadku prawie mu się to udało, bo zaproponował zakres D8:D128

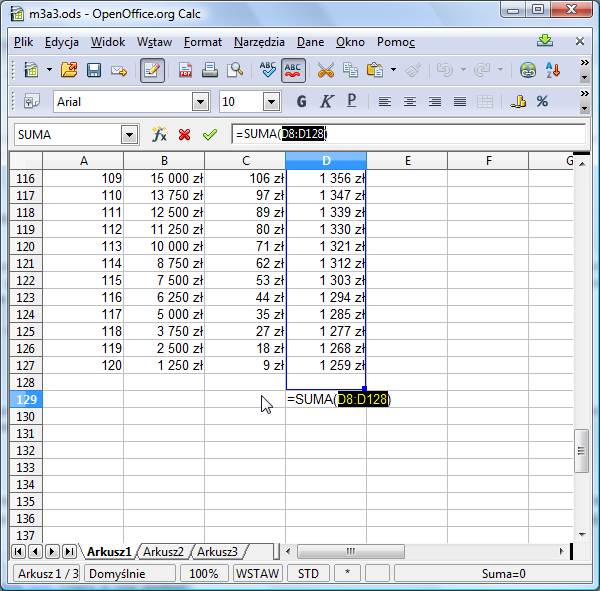
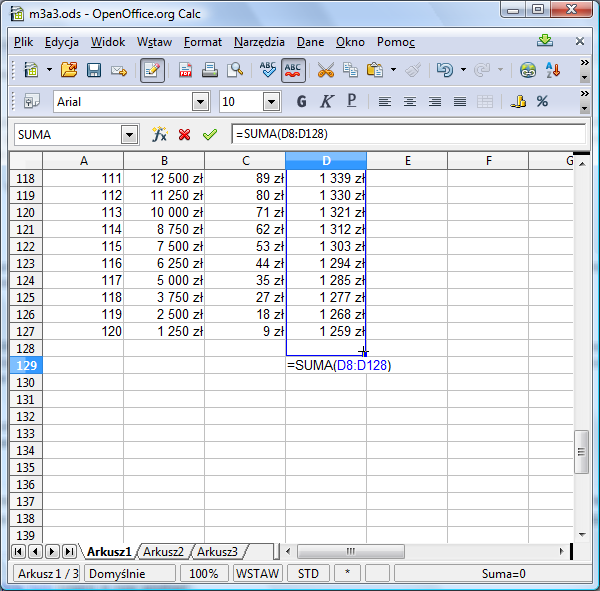
Poprawiamy go lekko tak, aby obejmował komórki od D8 do D127. W tym celu ustawiamy kursor myszki w prawym dolnym rogu zaznaczonego na niebiesko obszaru - kursor powinien zmienić kształt na krzyżyk i zmniejszamy zaznaczony zakres. Zwróć uwagę, aby kursor miał kształt krzyżyka! Kursor w kształcie dłoni powoduje przesunięcie (bez zmiany rozmiaru) zaznaczonego obszaru.

Ćwiczenie

Poeksperymentuj z wybieraniem do sumowania różnych fragmentów arkusza. Cały czas obserwuj, co pojawia się w polu edycji. Pamiętaj, że wciśnięcie klawisza Esc powoduje anulowanie zmian, a klawisz Enter zatwierdza wybór.

Po zatwierdzeniu wyboru klawiszem Enter powinniśmy zobaczyć kwotę 214 281 zł.

Ćwiczenie

O ile procent większa od kwoty kredytu będzie faktyczna suma rat? Wpisz odpowiednią formułę w komórkę B129.

Ćwiczenie

Zmień kwotę kredytu w C3 i oprocentowanie w C1. Zaobserwuj, że wszystkie komórki w przygotowanej właśnie przez Ciebie symulacji spłaty kredytu są automatycznie przeliczane.

A jak zmienić liczbę rat? Wymaga to niestety większych zmian. Trzeba wpisać odpowiednią wartość w pole C2 i wydłużyć lub skrócić tabelkę. Na przykład przy kredycie na 30 lat, liczba rat będzie wynosić 360 i tabelkę trzeba wydłużyć do 360 wierszy (przeciągając ostatni wiersz).

Ćwiczenie

Przesymuluj spłatę kredytu w 360 miesięcznych ratach przy oprocentowaniu 3,5% i kwocie kredytu 100 tysięcy złotych.

Symulacja spłaty kredytu przy stałych ratach

Czasami banki stosują nieco inną metodę obliczania raty kredytu: ustalają stałą miesięczną ratę. Kredytobiorca wpłaca wtedy co miesiąc tę samą kwotę. Jest ona przeznaczona przede wszystkim na spłatę odsetek, a to co pozostanie zmniejsza aktualne zadłużenie. Wielkość raty jest tak dobrana, aby po wpłacie ostatniej raty zadłużenie wyniosło 0.

W pewnym sensie mamy więc tutaj sytuację odwrotną do poprzedniego przykładu. Wtedy zadłużenie malało o stałą kwotę każdego miesiąca, a raty spłacane do banku zmniejszały się co miesiąc. Teraz spłaty są stałe, a zadłużenie maleje o zmienną kwotę (zwiększającą się z każdą kolejną ratą).

Chociaż wielkość raty można obliczyć mając dane oprocentowanie, liczbę rat i kwotę kredytu, to jednak na razie nie będziemy pokazywać, jak wykonać takie rachunki. Zamiast tego spróbujemy dobrać tę wielkością metodą prób i błędów przygotowując sobie odpowiedni arkusz kalkulacyjny.

Zacznijmy - tak jak poprzednio - od wpisania do arkusza "parametrów kredytu". Tym razem jednak nie będziemy obliczać raty kapitałowej w komórce C4, bo jest ona zmienna. Zamiast tego w C4 wpiszemy "zgadniętą" przez nas wielkość raty. Pamiętamy, że z w poprzednim modelu raty zmieniały się od 1259 zł do 2313 zł. Spróbujmy więc na początku przyjąć, że kredytobiorca co miesiąc płaci 2000 zł i sprawdźmy, jak przy takim założeniu zmienia się zadłużenie.

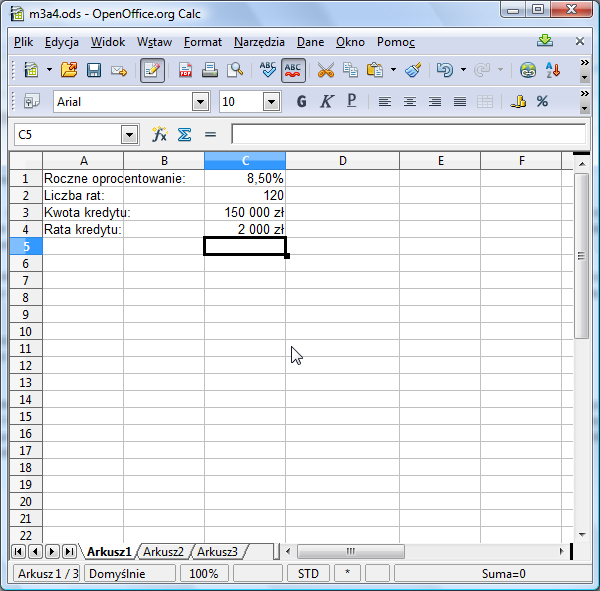
Sporządzamy, jak poprzednio tabelkę. W pierwszej kolumnie wpisujemy numer raty - przygotujmy sobie od razu wszystkie 120 pozycji. W drugiej kolumnie będziemy obliczać zadłużenie, a w trzeciej aktualne odsetki. W czwartej kolumnie będziemy obliczać aktualną ratę kapitałową. Formuła obliczająca zadłużenie w pierwszym wierszu jest taka jak poprzednio, analogicznie też oblicza się odsetki:

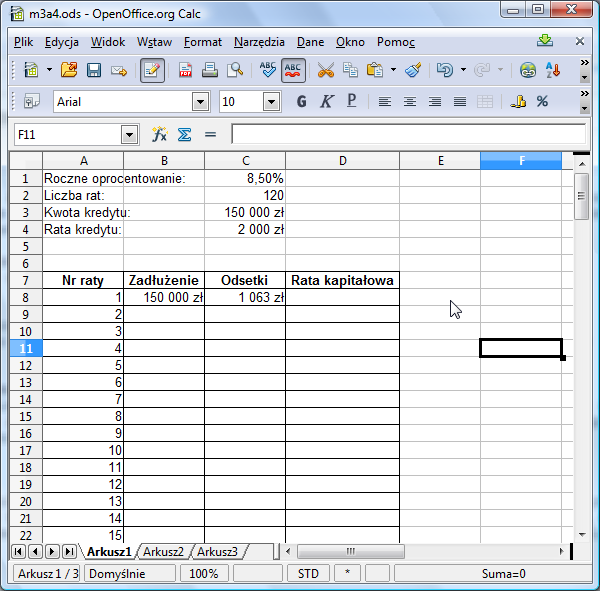
Wpiszmy teraz do komórki D8 formułę obliczającą ratę kapitałową. Wiemy, że całkowita wielkość raty to 2000 zł (zawartość komórki C4). Z tej kwoty 1063 zł idą na spłatę odsetek. Zatem rata kapitałowa wynosi 2000-1063=938 zł.

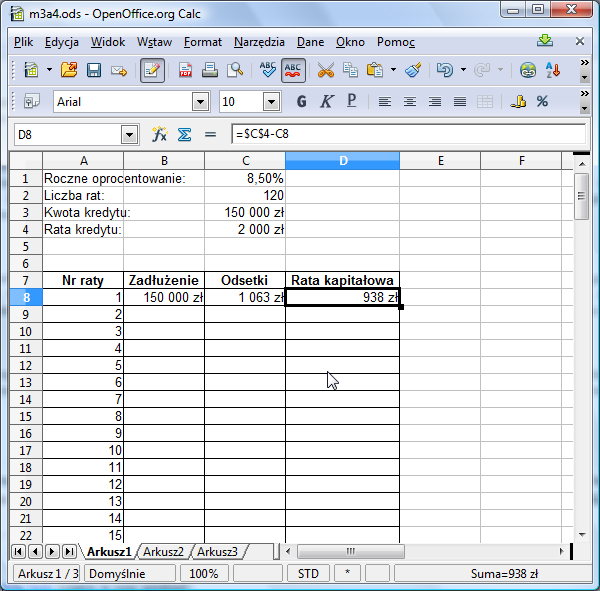
Zadłużenie zmniejsza się więc o 938 zł. Wpisujemy odpowiednią formułę do B9: =B8-D8. Następnie po kolei, jedna po drugiej, przeciągamy w dół do końca tabeli formuły z B9, C8 i D8. Nie przejmuj się, jeśli początkowo nic się nie będzie zmieniać w tabelce. Nabierze ona sensu, dopiero po wypełnieniu wszystkich komórek.

Przyjrzyjmy się teraz końcówce tabeli:

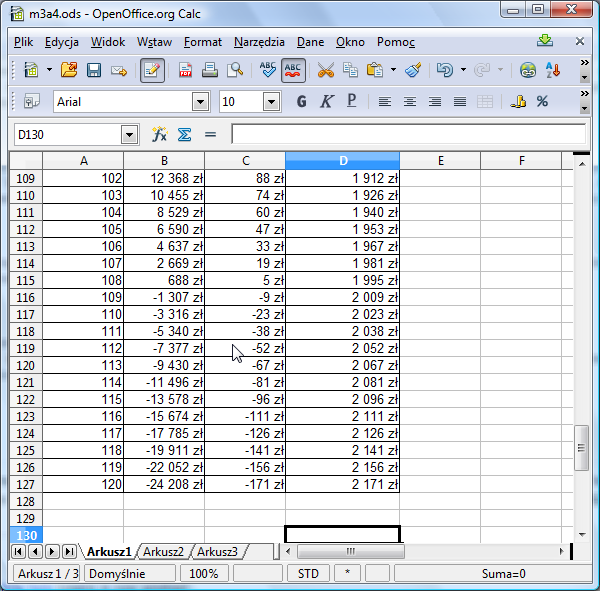
Zinterpretujmy wyniki. Przy 120 racie zadłużenie wynosi -24208 zł, a my jeszcze spłacamy 2171 zł! W efekcie spłacimy o 26380 zł za dużo (celowo formuła w kolumnie B została przeciągnięta aż do pozycji B128 - w tej komórce znajdzie się zadłużenie po 120 racie). Tak naprawdę kredyt został spłacony już w 108 racie - wtedy zadłużenie spadło poniżej zera. Oznacza to, że rata 2000 zł miesięcznie jest za wysoka. Za chwilę spróbujemy zmniejszyć ją do 1500 zł i sprawdzić, jakie wtedy będzie zadłużenie po 120 racie. Ponieważ jednak będziemy ciągle manipulować wartością z C4 i przyglądać się wartości w B128, dla wygody, aby widzieć jednocześnie obie te wartości, powielmy wartość z B128 w komórce E4:

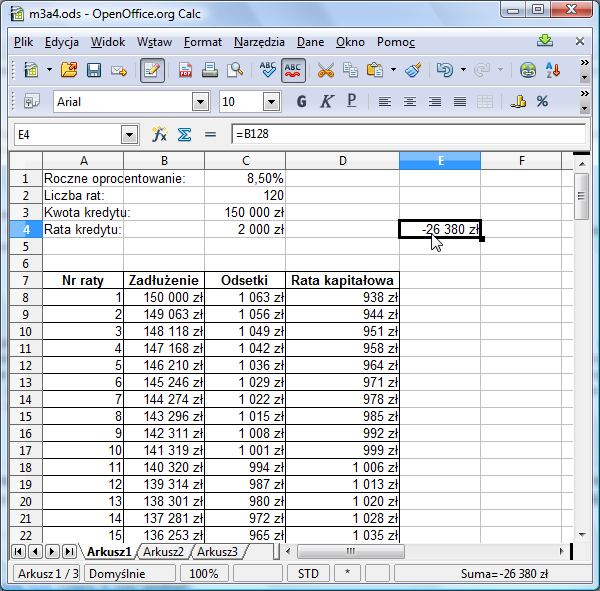
Na skutek zmiany raty z 2000 zł na 1500 zł, końcowe zadłużenie wyniosło 67689 zł. Zatem kredyt nie został spłacony - rata jest zbyt mała. Wypróbujmy kolejne wartości za każdym razem zwiększając lub zmniejszając ratę w zależności od wartości w polu E4 dążąc do tego, aby wartość w tym polu wyzerowała się. Spróbujmy wpisać kwotę znajdującą się "w połowie" między 1500 a 2000, czyli 1750:

Plik:M3a4p6.png

Dalej za mało. Między 1750 a 2000 jest 1875. Tym razem w E4 jest wartość ujemna, więc spróbujmy mniejszą ratę. Celujemy w wartość między 1750 a 1875, czyli w przybliżeniu 1813 zł. Okazuje się, że to za mało:

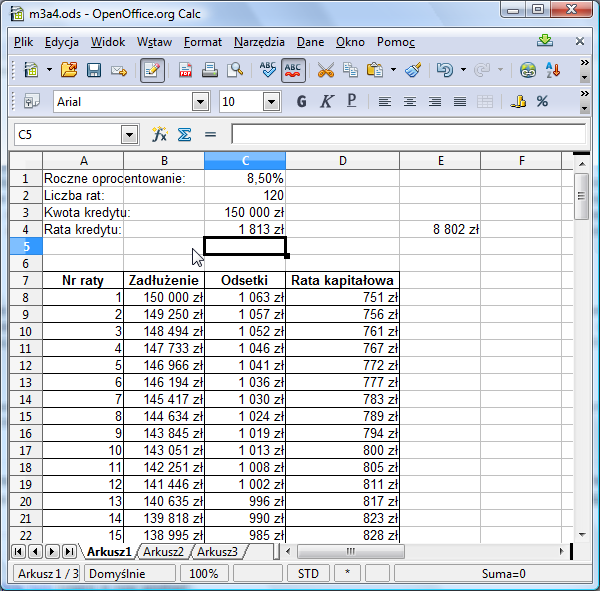
Próbując kolejno: 1844, 1860, 1852, 1856, 1858, 1859 dochodzimy do wniosku, że właściwa kwota jest między 1859 a 1860 zł. Metodą kolejnych prób można szybko ustalić, że dobrym przybliżeniem jest 1859,71 zł:

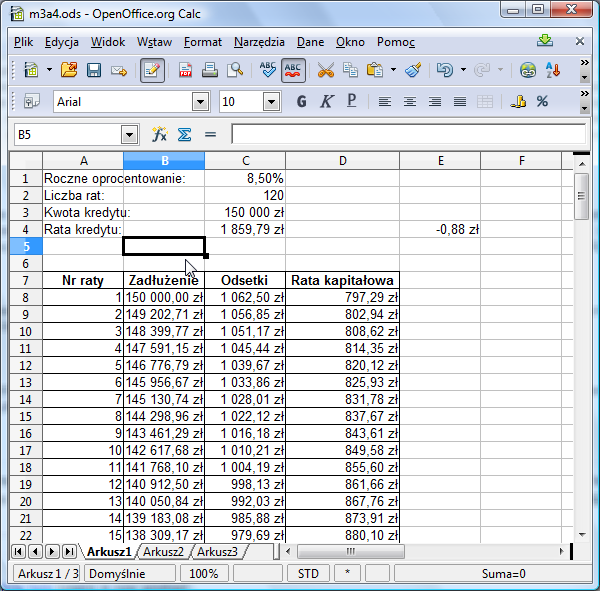
Sprawdź jeszcze, ile łącznie kredytobiorca zapłaci bankowi. Tym razem formuła jest prosta i nie wymaga sumowania:

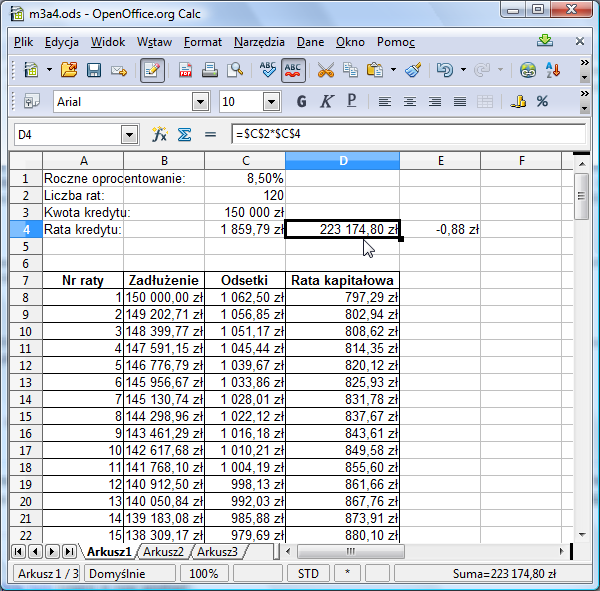
Tak naprawdę, aby wyznaczyć wielkość raty przy opisanym tu systemie spłaty nie trzeba wykonywać takich symulacji. Można ją wyliczyć korzystając ze wzoru kp(1+p)^n/((1+d)^n-1), gdzie k jest kwotą kredytu, a d jest miesięcznym oprocentowaniem, a n jest liczbą rat.

Ćwiczenie

Zapisz tę formułę w komórce C5 arkusza. Aby policzyć x^n należy użyć wyrażenia potęga(x;n).

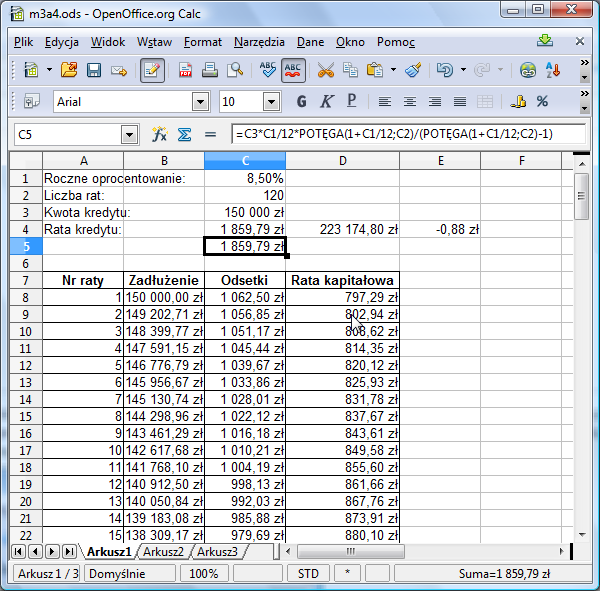
Adresowanie mieszane

Tabliczka mnożenia

Zmieńmy teraz tematykę. Chcemy wykonać za pomocą arkusza kalkulacyjnego ... tabliczkę mnożenia. Sformatuj odpowiednio arkusz. Zacznij od ustawienia szerokości pierwszych 11 kolumn. W tym celu zaznacz całe kolumny klikając na ich nagłówki (pola z literami) lewym klawiszem myszy i przesuwając myszkę przy wciśniętym lewym klawiszu myszy. Następnie kliknij na którykolwiek nagłówek prawym klawiszem myszy. Pojawi się menu podręczne:

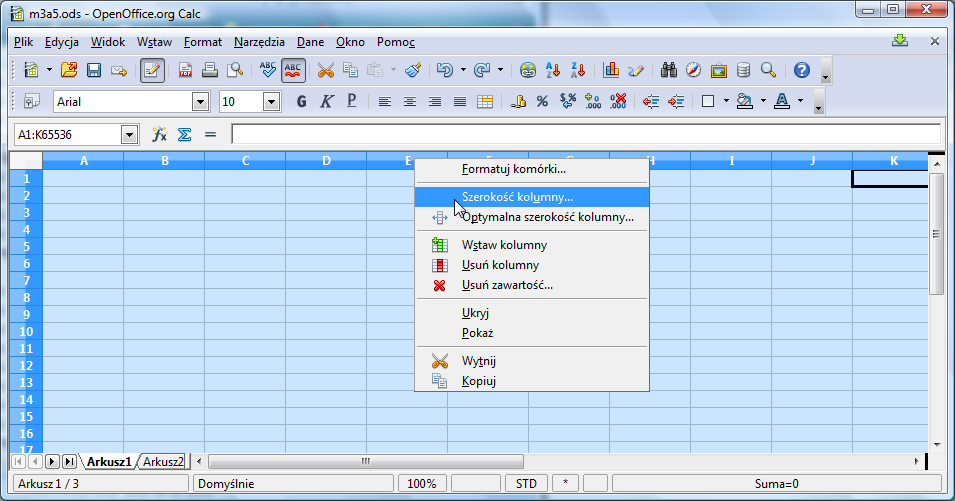
Wybierz z niego opcję Szerokość kolumny i wprowadź wartość 0,5cm:

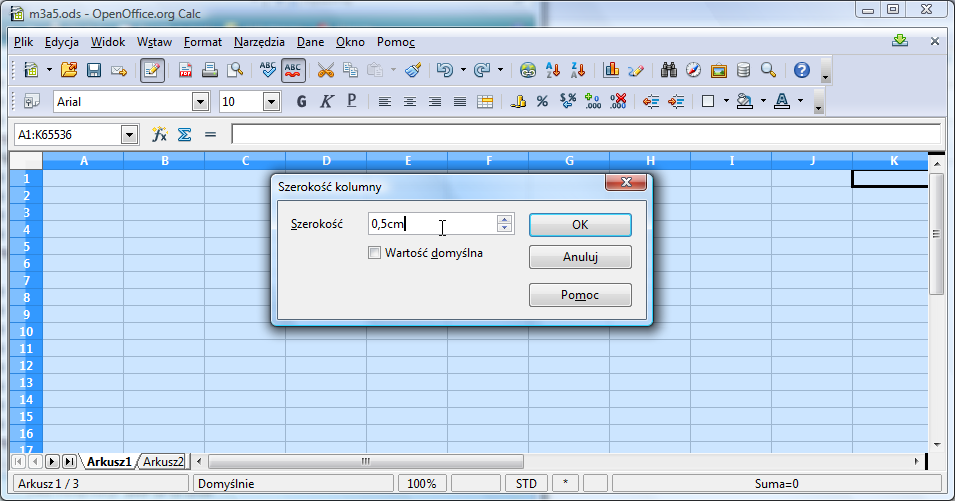
Ustaw kolor tła i krawędzie - wszystkie te opcje są dostępne z menu Formatuj komórki. Następnie stosując technikę przeciągania wypełnij pierwszą kolumnę i pierwszy wiersz wartościami od 1 do 10:

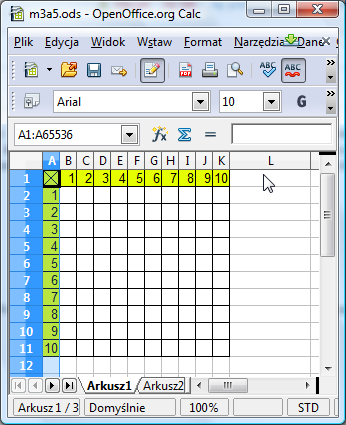
Teraz czas na najważniejszy element. Do komórki B2 trzeba wpisać formułę. Powinna ona być tak napisana, aby po jej przeciągnięciu w dół i w prawo, w arkuszu powstała tabliczka mnożenia. Z pozoru sprawa jest prosta - wpisujemy: =A2*B1. Jednak po przeciągnięciu formuły w dół otrzymujemy następującą tabelę:

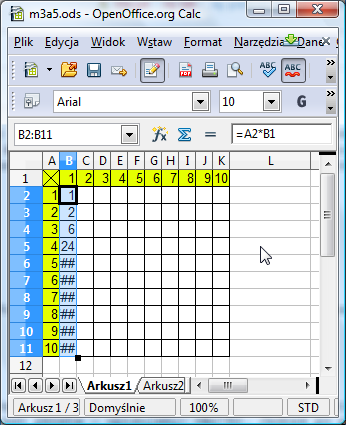
Krzyżyki w polu liczbowym oznaczają, że kolumna jest zbyt wąska, aby wyświetlić liczbę. Możemy się z tym uporać klikając podwójnie krawędź między kolumnami - ustawi to automatycznie optymalną szerokość kolumny. Jednak widać, że wartości, które zostały utworzone nie są tym, co chcieliśmy uzyskać:

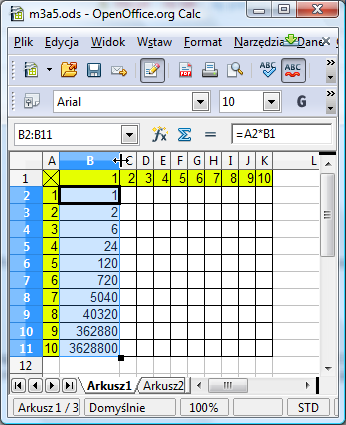
Oczywiście, błąd polegał na tym, że wprowadzając adres B1 użyliśmy adresowania względnego. Poprawmy zatem formułę na =A2*$B$1. Ciągniemy ją w dół - wszystko wygląda poprawnie:

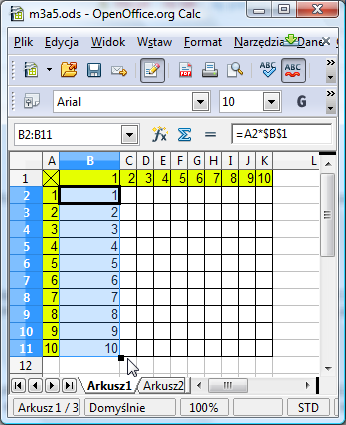
Teraz chwytamy myszką za kwadracik w prawym dolnym rogu zaznaczonego obszaru, ciągniemy w prawo i ... Niestety, wynik nie jest poprawny:

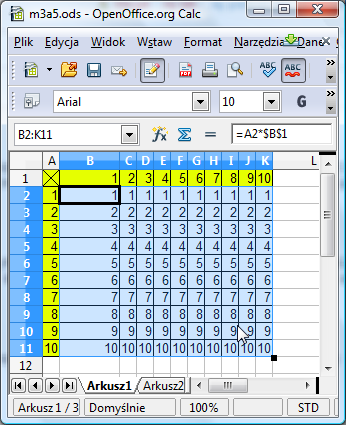
Dlaczego? Użyliśmy adresowania bezwzględnego - zatem we wszystkich komórkach w całej tabeli występuje mnożenie przez B1. Zdecydowanie nie o to chodziło.

Aby zrozumieć, jaka formuła jest tu potrzebna wyobraźmy sobie, że chcemy wpisać formułę do komórki E4. Pole to odpowiada mnożeniu 3 przez 4. Na pewno musi tu znaleźć się iloczyn komórek A4 i E1. Problemem jest jedynie sposób adresowania. Wyraźmy najpierw w języku polskim, co oznaczałyby różne sposoby adresowania A4 i E1:

• Adresowanie względne w postaci =A4*E1 oznacza, że chcemy przemnożyć przez siebie liczbę znajdującą się w tej samej kolumnie, ale trzy komórki do góry (E1) przez liczbę w tym samym wierszu, ale cztery komórki na lewo (A4). Jest to prawdą akurat dla komórki E4, ale po przekopiowaniu formuły o jedno pole w prawo lub dół, już nie będzie to zgodne z naszymi intencjami.
• Adresowanie postaci $A$4*E1 oznacza, że chcemy przemnożyć liczbę znajdującą się w pierwszej kolumnie i trzecim wierszu przez liczbę znajdującą się w tej samej kolumnie, ale trzy komórki do góry. I znów jest to prawda dla E4, ale przestaje być tym, co chcemy uzyskać w dowolnym wierszu innym niż trzeci.
• Tak naprawdę chcemy wyrazić następującą formułę: Przemnóż liczbę znajdującą się w tym samym wierszu, ale w pierwszej kolumnie przez liczbę znajdującą się w pierwszym wierszu tej samej kolumny . Słowa w tym samym sugerują adresowanie względne, słowo w pierwszym oznacza adres bezwzględny.

Przeanalizujmy jeszcze raz sformułowanie pierwsza kolumna tego samego wiersza. Oznacza ono, że do kolumn chcemy odwołać się w sposób bezwzględny, a do wierszy w sposób względny. Innymi słowy chcemy zablokować zmianę numeru kolumny przy przeciąganiu formuły w poziomie, ale zezwalać na zmianę numeru wiersza przy przeciąganiu formuły w pionie. Szczęśliwie w arkuszu można zapisać i taki sposób adresowania umieszczając znak $ jedynie przed tą składową adresu (literą lub liczbą), która ma być adresowana w sposób bezwzględny (albo inaczej: blokowana przy przeciąganiu). Zatem, jeżeli w formule wpisywanej do komórki E4 chcemy odwołać się do pierwszej kolumny tego samego wiersza napiszemy: $A4. Chcąc odwołać się do pierwszego wiersza tej samej kolumny napiszemy E$1.

Powyższe rozumowanie pokazuje, że formuła, która należy wpisać do E4 to =$A4*E$1. Analogicznie do B2 wpiszemy =$A2*B$1. Przetestujmy to w arkuszu. Wpisz podaną formułę do komórki B2, następnie przeciągnij ją w dół i w prawo. Faktycznie powstała tabliczka mnożenia!

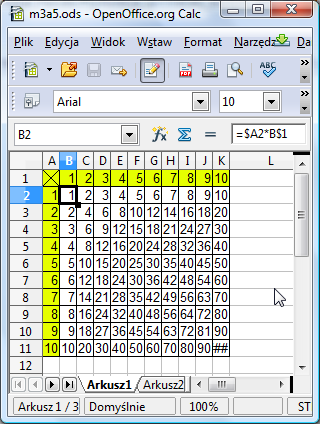
Zwróć uwagę, że liczba 100 w K11 nie mieści się w komórce - trzeba zwiększyć szerokość kolumny.

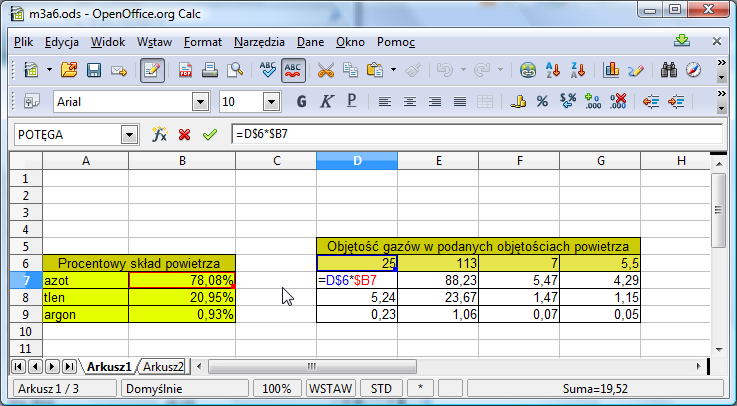
Skład powietrza

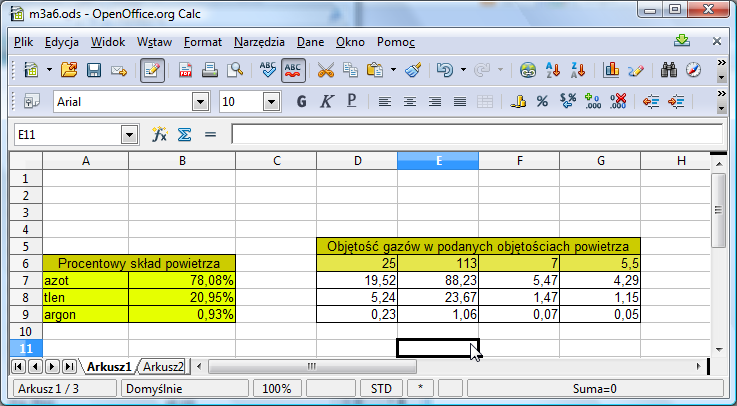
Adresowanie mieszane zaskakująco często pojawia się w różnych potrzebnych w praktyce arkuszach. Oto kolejny przykład. Chcemy dowiedzieć się, jaka jest objętość azotu, tlenu i argonu objętościach powietrze. Znajdujemy skład procentowy powietrza i sporządzamy następującą tabelę:

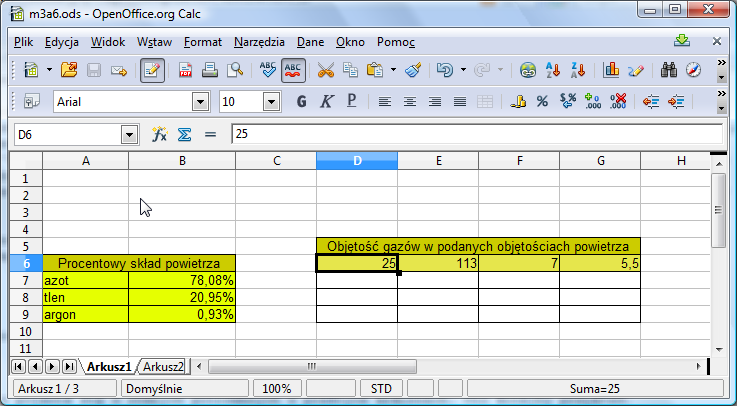
W komórkach B7:B9 mamy procentową objętość poszczególnych gazów w powietrzu, a w komórkach D6:G6 - interesujące nas objętości powietrza. Aby obliczyć objętość poszczególnych gazów w podanych objętościach powietrza wystarczy teraz wpisać odpowiednią formułę w pole D7, a następnie przeciągnąć ją do wszystkich pól w zakresie D7:G9 uzyskując poniższą tabelkę:

Ćwiczenie

Jaka to formuła?

Tak naprawdę zadanie to niewiele różni się od przykładu z tabliczką mnożenia. Oto rozwiązanie: