Ciągi - przykłady

Na początek przedstawimy kilka łatwych do opisania ciągów.

Często łatwiej jest sobie wyobrazić abstrakcyjny obiekt, jeśli można przedstawić go na rysunku. Dlatego na przykład rysujemy wykresy funkcji. Ciągi są przykładami funkcji, więc będziemy je rysować właśnie jako wykresy funkcji - wykorzystując prostokątny układ współrzędnych, a właściwie jego część.

Żeby narysować ciąg a_n, czyli wykres odpowiadającej mu funkcji, na osi OX będziemy potrzebować tylko punktów odpowiadających liczbom naturalnym. Na pionowej prostej x = n zaznaczamy punkt o drugiej współrzędnej y = a_n. Czyli wykres będzie się składał z pojedynczych punktów położonych nad kolejnymi liczbami naturalnymi. Zobaczmy, jak to wygląda dla niektórych z omawianych wcześniej przykładów.

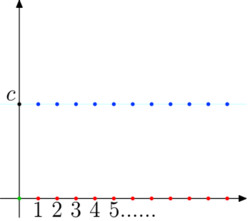
Ciąg stały a_n = c z przykładu 1.

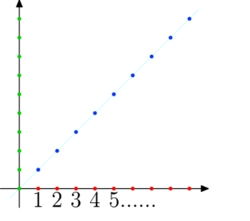
Ciąg identycznościowy b_n = n z przykładu 2.

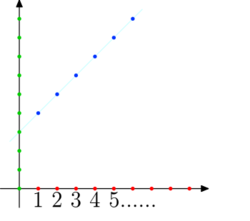
Ciąg identycznościowy przesunięty o 3 pozycje w lewo, czyli c_n = n + 3 z przykładu 3.

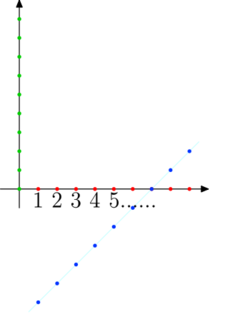
Ciąg identycznościowy przesunięty o 7 pozycji w prawo, czyli d_n = n − k dla k = 7 z przykładu 4.

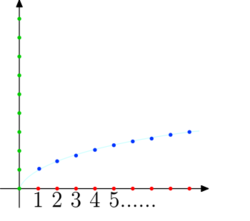
Ciąg \(f_n = \sqrt{n}\) z przykładu 6a.

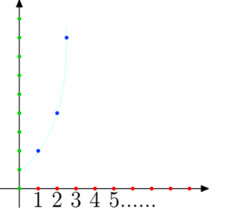
Ciąg g_n = 2ⁿ z przykładu 6b.

Zwykle wykres pozwala nabrać intuicji co do pewnych globalnych własności ciągu, czyli własności ciągu jako całości, a nie własności poszczególnych wyrazów. Na przykład można zaobserwować, czy ciąg jest monotoniczny, od początku lub dopiero od pewnego momentu. Jeśli tak, to widać, czy rośnie lub maleje szybko.

Ale trzeba pamiętać o tym, że rysunek nie jest dowodem własności ciągu, nawet jeśli wydaje nam się na przykład, że "z rysunku przecież jest całkiem oczywiste, że ten ciąg maleje!". Umiemy narysować tylko skończenie wiele wyrazów ciągu, a z nich nie możemy nic powiedzieć na pewno o własnościach całego ciągu. Chociażby dlatego, że ktoś mógłby złośliwie podmienić te wyrazy, których nie ma na rysunku, na wyrazy zachowujące się zupełnie inaczej...

Podobnie, nie można twierdzić, że zna się wzór opisujący wyrazy ciągu, jeśli widziało się tylko kilka wyrazów. Może te wyrazy pasują do jakiegoś ogólnego wzoru, ale to jeszcze nie znaczy, że dalej ta prawidłowość, która nasuwa się po obejrzeniu początku ciągu, jest zachowywana. Ani rysunek, ani informacja o początkowych wyrazach nie zawiera pełnej informacji o ciągu, co ilustruje zagadka.

a₁ = 1, a₂ = 2, a₃ = 4...?

Czasami ciąg jest zdefiniowany przez podanie kilku początkowych wyrazów i informację, w jaki sposób każdy dalszy wyraz można wyliczyć z poprzednich, czyli zależność rekurencyjną.

Najbardziej znany ciąg definiowany w ten sposób to ciąg Fibonacciego: a₁ = a₂ = 1, dla n > 2, a_n = a_{n − 1} + a_{n − 2}.

Zadanie 1. Wyznacz 10 początkowych wyrazów ciągu Fibonacciego.

a₁ = 1,

a₂ = 1,

a₃ = a₂ + a₁ = 1 + 1 = 2,

a₄ = a₃ + a₂ = 2 + 1 = 3,

a₅ = a₄ + a₃ = 3 + 2 = 5,

a₆ = a₅ + a₄ = 5 + 3 = 8,

i dalej a₇ = 13, a₈ = 21, a₉ = 34, a₁₀ = 55, a₁₁ = 89, a₁₂ = 144, a₁₃ = 233, a₁₄ = 377, a₁₅ = 610.

Jak widać, rośnie on dość szybko...

Zapisanie ciągu zdefiniowanego zależnością rekurencyjną jawnym wzorem, czyli takim, że we wzorze na n-ty wyraz pojawiają się tylko stałe i liczba n, a nie pojawiają się zależności od innych wyrazów ciągu, może być trudne, ale nie musi (zobacz zadanie 2). Zwykle jednak takiego wzoru nie można łatwo zgadnąć, znając definicję rekurencyjną, bo nie widać w nim struktury rekurencyjnej ciągu. (Dla pewnych szczególnych postaci wzorów rekurencyjnych opracowano metody przechodzenia do wzoru jawnego na wyrazy ciągu.)

Zadanie 2.

Definiujemy ciąg a₁ = 1, a₂ = 2, a_n = 2a_{n − 2} + a_{n − 1}. Jaki to jest ciąg? Jak go zapisać prościej?

\(a_3 = 2a_1 + a_2 = 2\cdot 1+2 = 4\),

\(a_4 = 2a_2 + a_3 = 2 \cdot 2+4 = 8\),...

Wygląda na to, że a_n = 2^{n − 1}. Ale na razie to tylko hipoteza - wiemy tylko, że kilka pierwszych wyrazów pasuje do wzoru. A żeby to udowodnić, należy użyć zasady indukcji.

1) Sprawdziliśmy już poprawność tezy dla małych wyrazów.

2) Załóżmy, że teza jest prawdziwa dla liczb naturalnych od 1 do n, dowodzimy dla n + 1. Korzystając na początku z założenia indukcyjnego, otrzymujemy

\(a_{n+1} = 2a_{n-1} + a_n = 2 \cdot 2^{n-2} + 2^{n-1} = 2 \cdot 2^{n-1} = 2^n,\)

więc na mocy zasady indukcji teza jest prawdziwa.

Problem 1. Spróbuj znaleźć wzór jawny opisujący ciąg Fibonacciego.

Przejście od wzoru jawnego do rekurencyjnego czasami bywa nietrudne, jak pokazuje zadanie 3. Czasami nie jest łatwe, a często pytanie o wzór rekurencyjny właściwie nie ma sensu, bo ładna formuła rekurencyjna opisująca dany ciąg może po prostu nie istnieć.

Zadanie 3.

Ciąg (a_n) jest dany wzorem \(a_n = \sqrt[2^n]{1794}\). Jaki wzór rekurencyjny opisuje ten ciąg?

Wobec tego zależność rekurencyjna definiująca ten ciąg to \(a_n = \sqrt{a_{n-1}}\), a do pełnej definicji ciągu brakuje jeszcze informacji, że \(a_1 = \sqrt[2]{1794}\).