Przyjrzyjmy się dwóm rodzajom ciągów o szczególnych własnościach.
|
Definicja 1. Ciąg arytmetyczny to ciąg (an), w którym różnice pomiędzy kolejnymi wyrazami są takie same: dla każdej liczby naturalnej n liczba an + 1 − an jest równa pewnej ustalonej liczbie r. Liczba r jest nazywana różnicą ciągu arytmetycznego (an). |
Każdy wyraz ciągu arytmetycznego możemy wyznaczyć, znając pierwszy wyraz i liczbę r - różnicę: an = a1 + r(n − 1).
1) Oczywiście \(a_1 = a_1 + 0\cdot (n-1)\).
2) Zakładamy, że udowodniliśmy tezę dla liczb mniejszych od n i dowodzimy dla n. Zauważmy, że an = an − 1 + r, więc, korzystając z założenia indukcyjnego,
an = an − 1 + r = a1 + r(n − 2) + r = a1 + r(n − 1).
A można od razu zapisać an jako \(a_n = a_n - a_{n-1} + a_{n-1} - a_{n-2} + \ldots + a_2 - a_1 + a_1\), dodając i odejmując wszystkie wyrazy ciągu o mniejszych indeksach. Teraz wystarczy odpowiednio ustawić nawiasy: \(a_n = (a_n - a_{n-1}) + (a_{n-1} - a_{n-2}) \ldots + (a_2 - a_1) + a_1\) i zauważyć, że wartość każdego nawiasu to właśnie r, a nawiasów jest oczywiście n − 1.
|
Definicja 2. Ciąg geometryczny to ciąg (an), w którym każdy wyraz poza pierwszym otrzymujemy z poprzedniego przez pomnożenie przez pewną stałą q, czyli dla wszystkich liczb naturalnych \(n \geq 2\) zachodzi wzór \(a_n = q\cdot a_{n-1}\). Liczba q jest nazywana ilorazem ciągu geometrycznego (an). |
Tak naprawdę chcielibyśmy powiedzieć, jak w definicji ciągu arytmetycznego, że ciąg (an) jest geometryczny, jeśli ilorazy kolejnych wyrazów są takie same: dla każdej liczby naturalnej n liczba \(\frac{a_{n+1}}{a_n}\) jest równa pewnej ustalonej liczbie r. Ale wtedy pojawia się problem, jeśli chcemy sprawdzić, czy ciąg (an) mający wyrazy równe 0 jest geometryczny. Ale tak naprawdę te definicje są prawie równie dobre, bo kłopotliwych ciągów geometrycznych, czyli mających wyrazy zerowe, jest niedużo. Są to wyłącznie ciągi, które mają iloraz równy 0. To oznacza, że ich pierwszy wyraz może być dowolny, ale dalej są już tylko zera. Wobec tego, żeby stosować powyższy warunek zamiast definicji 2, wystarczy najpierw wykluczyć możliwość, że badany ciąg ma od drugiego miejsca same zera.
Zauważmy, że jeśli (an) jest ciągiem geometrycznym, a \(q = \frac{a_{n+1}}{a_n}\) - ilorazem sąsiednich wyrazów w tym ciągu, to \(a_n = a_1 \cdot q^{n-1}\).
Albo można sprowadzić problem do sytuacji ciągu arytmetycznego, logarytmując wyrazy ciągu geometrycznego dostajemy ciąg arytmetyczny.
Dla ciągów tak porządnych, jak arytmetyczne i geometryczne możemy wyprowadzić kilka przydatnych wzorów.
Jest takie stare zadanie: obliczyć sumę liczb naturalnych od 1 do 1000... Na pierwszy rzut oka raczej pracochłonne niż trudne, ale można podejść do tego z pomysłem. Rozwiążmy ogólniejszy problem znalezienia sumy wszystkich liczb naturalnych od 1 do n.
Żeby to zrobić, wystarczy ustawić liczby w następujące pary: 1 i n, 2 i n − 1, 3 i n − 2... (jak na rysunku) Suma liczb w każdej z par jest równa n + 1. Mamy dwa przypadki.
1) Jeśli n jest parzysta, to każda liczba znajdzie się w jakiejś parze, a par będzie oczywiście \(\frac{n}{2}\). Wobec tego wynikiem jest \(\frac{n}{2}(n+1)\).
2) Jeśli n jest nieparzysta, to powstanie \(\frac{n-1}{2}\) par, a liczba w środku zbioru, czyli \(\frac{n+1}{2}\) pozostanie bez pary. Liczby w parach sumują się do \(\frac{n-1}{2}(n+1)\), a dodając \(\frac{n+1}{2}\) otrzymujemy... \(\frac{n+1}{2}(n-1 + 1) = \frac{n(n+1)}{2}\)!
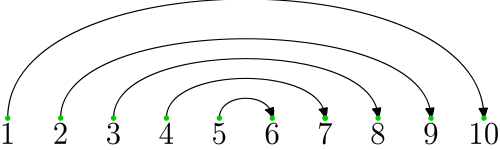
Połączenie liczb w pary dla n = 10
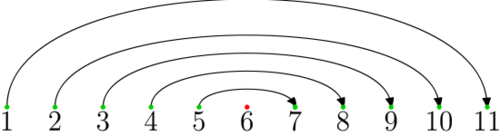
Połączenie liczb w pary dla n = 11
| Twierdzenie 1: |
|
Suma liczb naturalnych od 1 do n jest dana wzorem \(\frac{n(n+1)}{2}\) |
Postępując analogicznie, można obliczyć sumę dowolnego skończonego ciągu kolejnych liczb naturalnych, nie tylko zaczynającego się od 1. Ale tak naprawdę można zrobić o wiele więcej!
Okazuje się, że podobnie można wyprowadzić wzór na sumę kolejnych wyrazów dowolnego ciągu arytmetycznego (an).
Naszym celem jest zapisanie prostego wzoru na \(a_k + a_{k+1} + \ldots + a_{m-1} + a_m\). Tak jak poprzednio, łączymy wyrazy w pary: ak z am, ak + 1 z am − 1, a ogólnie ak + i z am − i, jeśli i jest takie, że k + i < m − i (inaczej, \(i < \frac{k+m}{2}\)).
Zauważmy, że ak + i + am − i = ak + am. Można to uzasadnić, zapisując wyrazy ciągu występujące w tym wzorze za pomocą a1 i różnicy r:
ak + am = a1 + r(k − 1) + a1 + r(m − 1) = a1 + r(k + i − 1) + a1 + r(m + i − 1) = ak + i + am − i.
Wobec tego sumy we wszystkich parach są równe. Tak jak powyżej, trzeba rozpatrzyć dwa przypadki, w zależności od parzystości liczby wyrazów, które sumujemy, i otrzymujemy wzór:
| Twierdzenie 2: |
|
Suma kolejnych wyrazów ciągu arytmetycznego (an) od am do ak wynosi \(\frac{(m-k+1)(a_k + a_m)}{2}\). |
Czasami przydaje się trochę inny zapis tego wzoru, korzystający tylko z wartości a1 i różnicy r:
\(\frac{(m-k+1)(a_k + a_m)}{2} = \frac{(m-k+1)(a_1 + (k-1)r + a_1 + (m-1)r)}{2} = a_1(m-k+1) + \frac{(m-k+1)(m+k-2)r}{2}\).
Sumę k początkowych wyrazów ciągu będziemy oznaczać przez Sk (lub Sk(an), jeśli trzeba będzie zaznaczyć, o jakim ciągu mówimy): \(S_k = a_1 + a_2 + \ldots + a_{k} = \sum_{n=1}^{k} a_n\).
Z twierdzenia 2 wynika wzór, który warto zapamiętać:
| Twierdzenie 3: |
|
Jeśli (an) jest ciągiem arytmetycznym, to \(S_k(a_n) = \frac{k(a_1+a_k)}{2}\). |
Znów można to zapisać, używając tylko a1 i różnicy r:
\(S_k(a_n) = ka_1 + \frac{rk(k-1)}{2}\).
Najpierw przydatny wzór na sumę kolejnych potęg danej liczby:
\(1 + x + x^2 + x^3 + \ldots + x^n = \frac{x^{n+1} - 1}{x - 1}\).
Żeby policzyć sumę k początkowych wyrazów ciągu geometrycznego (an) o ilorazie q, korzystamy ze wzoru an = a1qn − 1.
\(S_n = \sum_{n=1}^k a_n = \sum_{n=1}^k a_1 q^{n-1} = a_1 \sum_{n=1}^k q^{n-1} = a_1 \frac{q^n - 1}{q-1}\).
| Twierdzenie 4: |
|
Jeśli ciąg (an) jest ciągiem geometrycznym o ilorazie q, to \(S_n = a_1 \frac{q^n - 1}{q-1}\). |
Łatwo stąd wprowadzić wzór na sumę kolejnych wyrazów ciągu od am do ak, odejmując Sk − 1 od Sm (oczywiście musi być \(m \geq k\)): \(a_k + \ldots + a_m = S_m - S_{k-1} = \frac{a_1}{q-1}(q^m - q^{k-1}) = \frac{a_1 q^{k-1}}{q-1}(q^{m-k+1} - 1)\).
Dla ciągu arytmetycznego wypisywanie wzoru na iloczyn kolejnych elementów nie ma większego sensu - można to potraktować jako (męczące) zadanie...
Niech (an) będzie ciągiem geometrycznym. Chcemy wyznaczyć iloczyn \(a_k \cdot a_{k+1} \cdots a_{m-1}\cdot a_m\). Postępujemy właściwie tak samo, jak w przypadku ciągu arytmetycznego: łączymy w pary wyrazy ak + i z am − i i zauważamy, że iloczyn wyrazów w każdej parze jest równy \(a_k\cdot a_m\). Po nietrudnych obliczeniach (to dobre zadanie!) otrzymujemy
| Twierdzenie 5: |
|
Iloczyn kolejnych wyrazów ciągu geometrycznego (an) od am do ak wynosi \((\sqrt{a_k a_m})^{m-k+1}\). |
Można też zapisać ten wzór, używając tylko a1 i ilorazu q: iloczyn kolejnych wyrazów od am do ak jest równy \(a_1^{m-k+1}q^{\frac{(m+k-2)(m-k+1)}{2}}\).
