Jedna z najprostszych funkcji przypisuje liczbie x liczbę x. Funkcja taka jest oczywiście określona wzorem:
\(f\left(x\right)=x,\)
a jej wykresem jest linia prosta y=x złożona z punktów, których obie współrzędne są równe.
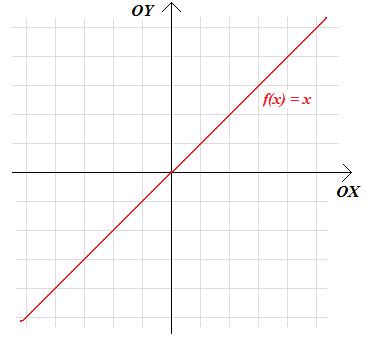
Zauważmy teraz, że korzystając z przekształceń wykresu opisanych w poprzedniej części, możemy z wykresu funkcji f(x)=x uzyskać całą serię wykresów innych funkcji:
- poprzez rozciąganie i ściskanie wykresu funkcji f(x)=x w kierunku pionowym lub poziomym otrzymujemy wykresy funkcji postaci g(x)=ax dla a > 0:
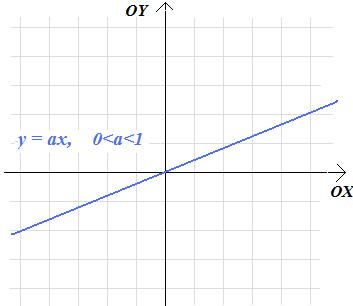
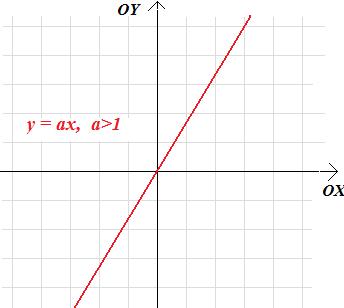
- odbicie względem osi OX (lub osi OY) wykresu funkcji f(x)=ax dla a > 0 daje nam z kolei wykresy funkcji g(x)=ax dla a<0:
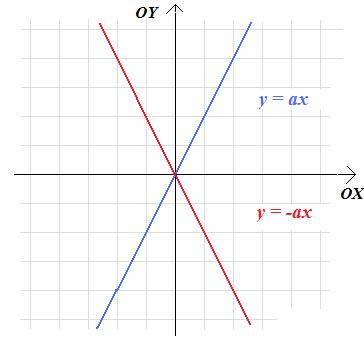
- przesunięcie o wektor [0;b] pozwala z wykresu funkcji g(x)=ax uzyskać wykres funkcji h(x)=ax+b:
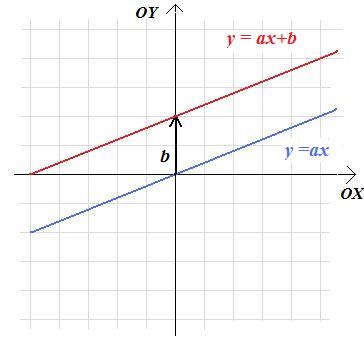
Funkcje, których wykresy powstają w drodze powyższych przekształceń nazywane są (razem z funkcjami stałymi) funkcjami liniowymi.
|
Definicja 3.1. Funkcję daną wzorem: \(f\left(x\right)=ax+b,\) gdzie a i b to pewne liczby rzeczywiste, nazywamy funkcją liniową. Liczbę a nazywamy współczynnikiem kierunkowym, natomiast liczbę b - wyrazem wolnym.
|
Zachodzą trzy podstawowe twierdzenia.
Twierdzenie 3.2. Wykresem funkcji liniowej jest linia prosta.
Twierdzenie 3.3. Prosta y=ax+b jest nachylona do osi OX pod kątem α takim, że tg(α) = a
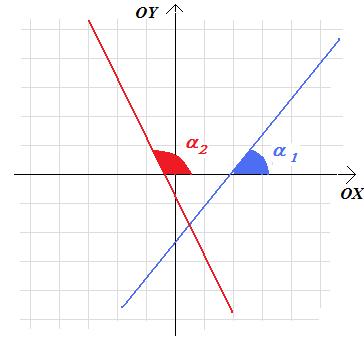
Twierdzenie 3.4. Funkcja liniowa f(x)=ax+b jest - rosnąca, gdy a>0; - stała, gdy a=0; - malejąca, gdy a<0.
Zadania
Zadanie 3.1. Narysuj wykresy funkcji:
a. \(f(x)=\frac14 x\) b. \(f(x)=\frac12 x\) c. \(f\left(x\right)=2x\) d. \(f\left(x\right)=4x\)
Rozwiązanie. Ponieważ wykresem funkcji f jest linia prosta, więc wystarczy znaleźć dwa punkty, przez które prosta ta przechodzi.
Do wykresu f należą punkty:
a. (0;0) oraz (4;1); b. (0;0) oraz (2;1); c. (0;0) oraz (1;2); d. (0;0) oraz (1;4).
A zatem wykresy rozważanych funkcji wyglądają następująco:
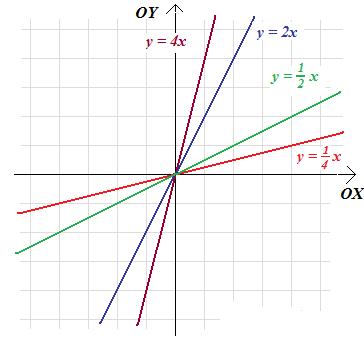
Widzimy, że gdy współczynnik a jest dodatni, to nachylenie prostej jest tym większe im większa jest liczba a.
Zadanie 3.2. Narysuj wykres funkcji:
a. \(f(x)=-\frac{1}{4} x\) b. \(f(x)=-\frac{1}{2} x\) c. \(f\left(x\right)=-2x\) d. \(f\left(x\right)=-4x\)
Rozwiązanie: I sposób. Do wykresu funkcji f należą punkty:
a. (0;0) oraz (-4;1); b. (0;0) oraz (-2;1); c. (0;0) oraz (1;-2); d. (0;0) oraz (1;-4).
A zatem wystarczy przez wymienione punkty poproawdzić proste.
Rozwiązanie II sposób. Odbijamy wykresy z zadania 3.1 względem osi OY, bowiem:
\(f\left(x\right)=-ax=-(ax)\)
Rozwiązanie III sposób. Odbijamy wykresy z zadania 3.1 względem osi OX, bowiem:
\(f\left(x\right)=-ax=a(-x)\)
Wykresy rozważanych funkcji wyglądają następująco:
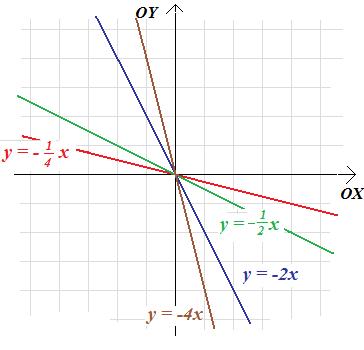
Zauważmy, że im bardziej ujemny jest współczynnik a (to znaczy im bardziej jest na osi liczbowej oddalony od zera), tym bardziej stroma jest prosta stanowiąca wykres funkcji.
Zadanie 3.3. Narysuj wykres funkcji:
a. \(f(x)=\frac13x+1\); b. \(f\left(x\right)=-2x-3\).
Rozwiązanie. Wykres funkcji:
\(f\left(x\right)=ax\)
po przesunięciu o wektor [0;b] staje się wykresem funkcji:
\(g\left(x\right)=ax+b.\)
A zatem:
a. przesuwamy prostą: \(y=\frac13 x\)
o jedną jednostkę do góry.
b. Przesuwamy prostą: y = − 2x
o trzy jednostki w dół.
Otrzymujemy w ten sposób następujące wykresy:
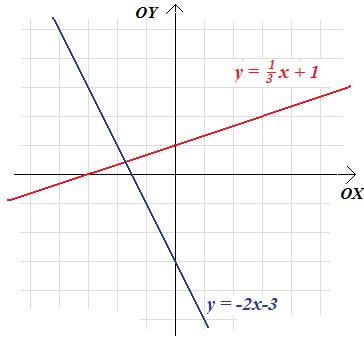
Zadanie 3.4. Wykres funkcji liniowej f przechodzi przez punkty (1;3) oraz (2;-1). Jaki wzór ma funkcja f?
Rozwiązanie. Funkcja f jest liniowa więc ma postać:
\(f\left(x\right)=ax+b,\)
gdzie liczby a oraz b nie są znane. Wiemy jednak, że:
f(1)=3 oraz f(2)=-1.
Musi zatem być spełniony układ równań:
\(\left \{ \begin{array}{cc} 3 = & a\cdot 1 + b \\ -1 = & a\cdot 2 + b \\ \end{array}\right .\)
Rozwiązujemy go dowolną metodą, uzyskując: a = − 4 oraz b=7. Stąd wzór funkcji to f(x)=-4x+7.
Zadanie 3.5. Narysuj wykres funkcji f określonej wzorem:
\(f(x)= \left\{ \begin{array}{cc} x-1, & gdy\;\;\;x\geq 3 \\ -x+5, & gdy \;\;\;x < 3 \\ \end{array} \right.\)
i znajdź zbiór argumentów x, dla których f(x) < 3.
Rozwiązanie. Poczynając od punktu (3;2) włacznie w kierunku strzałki osi OX (czyli na prawo), wykreślamy prostą y=x-1. Następnie od punktu (3;2) na lewo prowadzimy prostą y=-x+5. Wykres funkcji f wygląda zatem następująco:
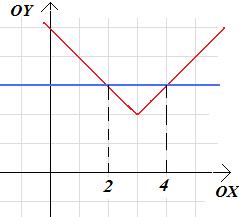
Zauważamy teraz, że wykres funkcji f przecina prostą y=3 w punktach: (2;3) oraz (4;3). Stąd f(x) < 3 dla \(x \in (2;4).\)
Uwaga. Zauważmy, że funkcję f możemy też określić jednym wzorem, korzystając z pojęcia wartości bezwzględnej:
\(f\left(x\right)=|x-3|+2\)
Zadanie 3.6. Wykres funkcji f(x) = 2x odbito symetrycznie względem prostej y = 2,uzyskując wykres funkcji g. Jaki wzór ma ta funkcja?
Rozwiązanie. Obraz wykresu f rozważanej symetrii przejdzie przez punkty A = (1;2) oraz B = (0;4). Równanie prostej przechodzącej przez punkty A i B to:
y = − 2x + 4.
A zatem:
g(x) = − 2x + 4.
Zadanie 3.7. Narysuj wykres funkcji:
\(f\left(x\right)=||2x-4|-2|\)
i znajdź wszystkie miejsca zerowe f.
Rozwiązanie. Kolejno rysujemy wykres funkcji:
1) h(x)=2x-4,
2) k(x)=|2x-4|,
3) l(x)=|2x-4|-2
i wreszcie wykres funkcji f.
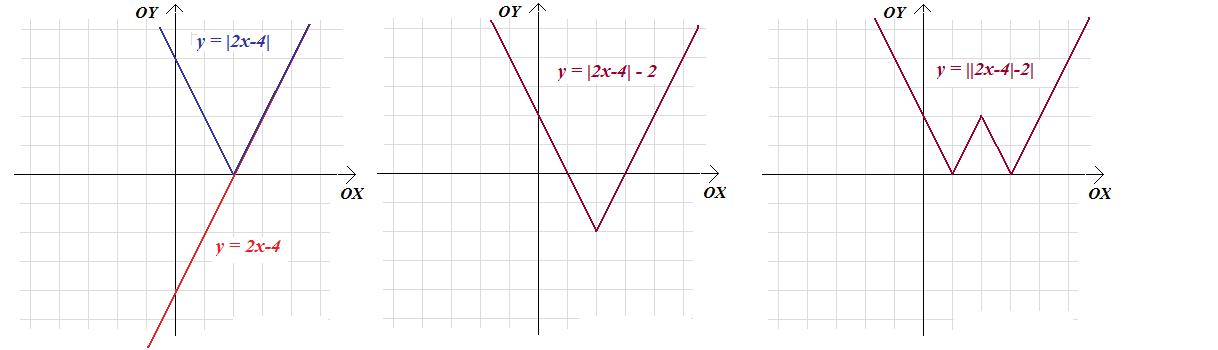
Miejsca zerowe f znajdujemy rozwiązując odpowiednie równanie:
\(f(x)=0 \Leftrightarrow ||2x-4|-2|=0 \Leftrightarrow |2x-4|=2 \Leftrightarrow |x-2|=1 \Leftrightarrow x=1 \;\;\rm lub\;\; x = 3.\)
Zadanie 3.8. Wykres funkcji f(x)=2x-3 odbito symetrycznie względem prostej y=2x+11. Jaki wzór ma funkcja g, której wykres uzyskano?
Rozwiązanie. Prosta y=2x+11 jest równoległa do prostej y=2x-3, bo powstaje z niej przez przesunięcie o 14 jednostek w górę. Prosta y=g(x) musi być więc także równoległa do prostej y=2x+11 i aby była od niej w tej samej odległości co prosta y=2x-3 musi powstać przez przesunięcie prostej y=2x+11 o 14 jednostek w górę. Stąd g(x)=2x+25.
Zadanie 3.9. Wykres funkcji: f(x)=3x odbito symetrycznie względem prostej y=x, uzyskując wykres funkcji g. Znajdź wzór funkcji g.
Rozwiązanie. Mamy oczywiście g(0)=0. Ponadto punkt (1;3) jest symetryczny do punktu (3;1) względem prostej y=x, więc g(3)=1:
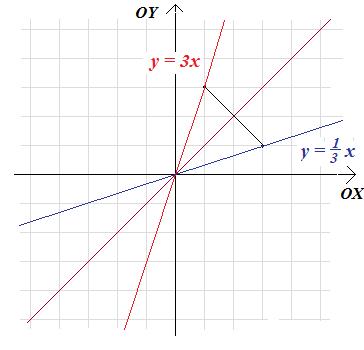
Wiedząc, że wykres funkcji g przechodzi przez punkty (0;0) oraz (3;1) łatwo zauważamy, że:
\(g(x)=\frac13 x.\)
Zadanie 3.10. Znajdź funkcję odwrotną do funkcji f(x)=ax+b, gdzie \(a\neq 0\).
Rozwiązanie. Niech y=ax+b i \(a \neq 0\). Wtedy:
\(x=\frac{y-b}{a}\).
A zatem funkcja odwrotna do f dana jest wzorem:
\(f(y)=\frac{1}{a}y-\frac{b}{a}\)
Jak widać, jest to także funkcja liniowa. Fakt ten ma prostą interpretację geometryczną. Mianowicie: linia y=ax+b jest symetryczna do prostej:
\(y=\frac{1}{a} x+\frac{b}{a}\)
względem prostej y=x.
Zadanie 3.11. Narysuj wykres funkcji:
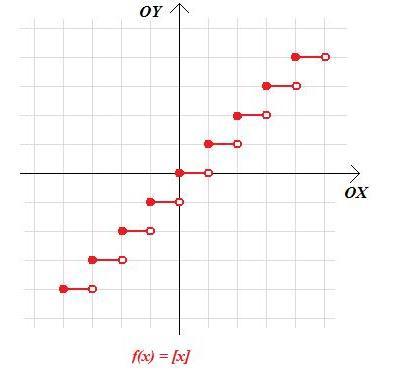
a. f(x) = [x]
b. f(x) = x − [x]
Rozwiązanie. a. Zauważamy, że na każdym przedziale [z;z+1), gdzie z jest liczbą całkowitą funkcja f jest stała (i równa z).
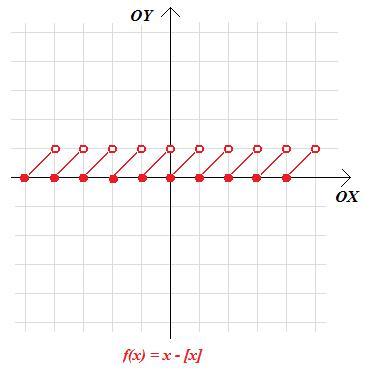
b. Zauważamy, że na każdym przedziale [z;z+1), gdzie z jest liczbą całkowitą funkcja f ma postać: f(x)=x-z.
Zadanie 3.12. Narysuj wykres funkcji:
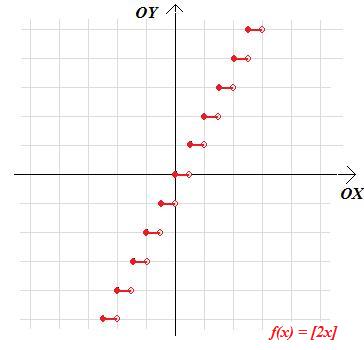
a. f(x) = [2x]
b. f(x) = 2[x]
Rozwiązanie.
W przypadku a ściskamy wykres funkcji f(x)=[x] dwa razy w kierunku poziomym.
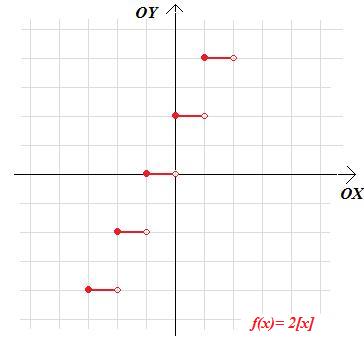
W przypadku b. rozciągamy wykres funkcji f(x)=[x] dwukrotnie w kierunku pionowym.
Zadanie 3.13. Wykres funkcji:
\(f(x)=\sqrt{3}x+1\)
obrócono o 120 stopni wokół punktu A=(0;1), w kierunku przeciwnym do ruchu wskazówek zegara, uzyskując wykres funkcji g. Jaki wzór ma funkcja g?
Rozwiązanie. Prosta \(y=\sqrt{3}x+1\) jest nachylona do osi OX pod kątem: \(60^\circ\), gdyż:
\(tg(60^{\circ})=\sqrt3\).
A zatem po obrocie wokół A o 120 stopni w kierunku przeciwnym do ruchu wskazówek zegara uzyskana prosta stanie się równoległa do osi OX.
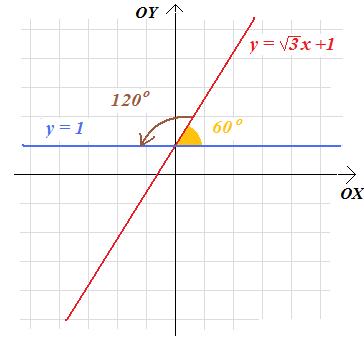
A zatem prosta ta będzie wykresem funkcji g(x) = 1.
Zadanie 3.14. Wykres funkcji f(x)=x+1 przesunięto o wektor [1;2] a następnie obrócono o 90 stopni wokół punktu (0;2), uzyskując wykres funkcji g. Znajdź miejsca zerowe funkcji g.
Rozwiązanie. Po przesunięciu o wektor [1;2] wykres funkcji f(x)=x+1 staje się wykresem funkcji:
\(g\left(x\right)=f(x-1)+2=(x-1)+1+2=x+2\)
Jeśli teraz obrócimy prostą y=x+2 wokół punktu (0;2) - leżącego na tej prostej - o 90 stopni, to uzyskamy pewną nową prostą k o równaniu y=ax+b. Kąt nachylenia prostej k jest równy: 135 stopni:
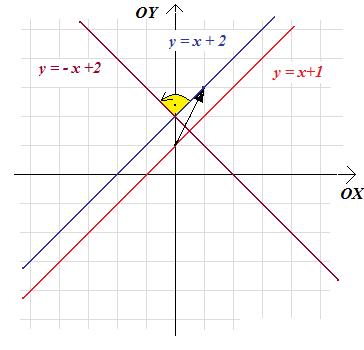
Stąd: \(a=tg(135^{\circ})=-1\). Ponadto punkt (0;2) należy do prostej k, więc b=2. Stąd g(x)=-x+2. Teraz łatwo znajdujemy miejsce zerowe funkcji g:
\(-x+2=0 \Leftrightarrow x=2.\)
Zadanie 3.15. Wykres funkcji: f(x) = a2x jest linią prostopadłą do wykresu funkcji g(x) = a1x. Jaki wzór ma funkcja f?
Rozwiązanie. Spójrzmy na rysunek:
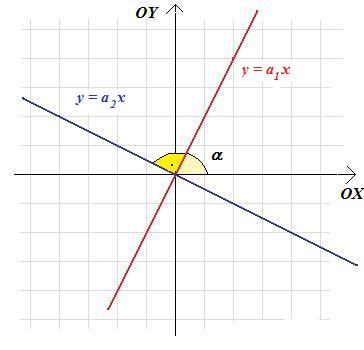
Mamy:
\(tg\left(\alpha\right)=a_1\) oraz \(tg(90^\circ+\alpha)=a_2\).
Stąd:
\(a_2=tg(90^{\circ}+\alpha)=-ctg(\alpha)=-\frac{1}{a_1}\)
Zadanie 3.16. Wykres funkcji:
\(f\left(x\right)=ax+b\)
przecina wykres funkcji:
\(g\left(x\right)=\frac13x+1\)
w punkcie (3;2) pod kątem prostym. Znajdź a oraz b.
Rozwiązanie. Z poprzedniego zadania wynika, że każda prosta prostopadła do prostej \(y=\frac13x\) (a zatem także do prostej \(y= \frac13x+1\) ma równanie y = − 3x + b. Stąd a=-3. Współczynnik b znajdujemy, korzystając z tego, że szukana prosta przechodzi przez punkt (3;2), a więc spełnia równanie:
\(2=-3\cdot2+b\)
Stąd b=8.
