Ciągi rozbieżne do nieskończoności

wt., 09/14/2010 - 09:32 — ciebie

Niektóre ciągi, chociaż nie są zbieżne do żadnej liczby rzeczywistej, zachowują się trochę podobnie jak ciągi zbieżne. Mianowicie, dążą do nieskończoności - do $+\infty$ lub $-\infty$.

Intuicja

Wyrazy ciągu zbieżnego muszą być ogólnie coraz bliżej granicy, chociaż zwykle nie dążą do niej w jakiś regularny sposób

(na przykład monotonicznie). Podobnie, ciągi rozbieżne do nieskończoności są coraz bliżej nieskończoności, czyli coraz dalej od małych liczb (tzn. o małej wartości bezwzględnej). Dokładniej, taki ciąg powinien spełniać warunek, że dla dowolnie wybranej liczby wszystkie wyrazy ciągu począwszy od pewnego miejsca są od niej większe, jeśli ciąg jest rozbieżny do $+\infty$, lub mniejsze, jeśli jest rozbieżny do $-\infty$.

Żeby to zapisać porządnie, trzeba użyć podobnej notacji, jak w definicji zwykłych granic.

Definicja 1.

Powiemy, że ciąg  $(a n)$  jest rozbieżny do plus nieskończoności, jeśli dla dowolnej liczby rzeczywistej  $K$

istnieje $n_0\in \mathbb{N}$ takie, że dla każdego $n > n 0$ zachodzi $a n > K$ .

Natomiast ciąg $(a n)$ jest rozbieżny do minus nieskończoności, jeśli dla dowolnej liczby rzeczywistej $M$ istnieje $n_0\in \mathbb{N}$ takie, że dla każdego $n > n 0$ zachodzi $a n < M$ .

Sformułowanie "ciąg rozbieżny do nieskończoności" oznacza, że dany ciąg spełnia któryś wariant definicji.

Jak widać wprost z definicji, ciągi rozbieżne do nieskończoności nie są ograniczone, ani nawet nie mogą mieć ograniczonego podciągu.

Ta definicja jest na tyle podobna do definicji zwykłej (czyli właściwej) granicy ciągu, że nasuwa się określenie ciągi zbieżne do nieskończoności. Ale tak się zazwyczaj nie mówi. Wyrazy ciągów rozbieżnych do nieskończoności dla dużych indeksów są zwykle dość daleko od siebie i nie skupiają się blisko żadnej liczby rzeczywistej, więc określenie "zbieżność" byłoby tu trochę nie na miejscu...

Przykład 1.

Wykażemy, że ciąg $a_n = \sqrt[6]{n}$ jest rozbieżny do $+\infty$.

Weźmy dowolną liczbę rzeczywistą $K > 0$ .

Żeby udowodnić rozbieżność do $+\infty$, wystarczy sprawdzić warunek z definicji tylko dla $K > 0$ , lub ogólniej, tylko dla $K$ większych od pewnej ustalonej liczby (podobnie jak w przypadku skończonej granicy interesowały nas tylko małe wartości $ε$ ). A nawet wystarczy sprawdzić warunek tylko dla liczb naturalnych większych od pewnej wybranej - czy umiesz to uzasadnić?

Chcemy udowodnić, że od pewnego miejsca wyrazy ciągu $(a n)$ są większe niż $K$ . Zastanówmy się więc, jak określić to miejsce w ciągu, od którego zachodzi nierówność $a n > K$ . Nierówność $a_n = \sqrt[6]{n} > K$ jest równoważna nierówności $n > K 6$ , ponieważ $K$ jest liczbą dodatnią. Mamy więc warunek, jaki musi spełniać $n$ , żeby $a n > K$ . Jeśli zdefiniujemy $n 0$ jako $\lceil K \rceil^6$, to dla wszystkich $n > n 0$ żądana nierówność będzie spełniona.

Uwaga: $\lceil x \rceil$ to funkcja sufit - oznacza najmniejszą liczbę całkowitą nie mniejszą niż $x$ (czyli idziemy z $x$ do góry, o mniej niż 1, do najbliższej liczby całkowitej).

Przykład 2.

Podobnie (a może nawet prościej) można wykazać, że ciągi $b n = n$ , $c_n = n^7 + \frac{1}{n^8}$, $d n = n!$ , $e_n = \frac{n^2 - 3n + 8}{2n + 7}$ są rozbieżne do $+\infty$.

Ciąg $(f n)$ zdefiniowany następująco: dla $n$ parzystych $f n = n 2 < m a t h > , a d l a < m a t h > n$ nieparzystych $f n = 2 n!$ również jest rozbieżny do $+\infty$. Nie jest natomiast monotoniczny, a nawet można powiedzieć, że jest bardzo daleki od monotoniczności (wygląda mniej więcej tak, jak na rysunku).

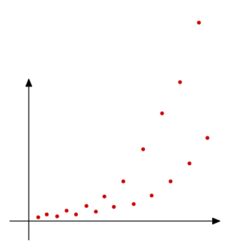
Przykład 3.

Ciągi $g n = - 17 n + 100$ , $h n = - 2 n$ , $i_n = -\sqrt{n}$ to przykłady ciągów rozbieżnych do $-\infty$.

Zadanie 1. Udowodnić, że ciąg $a n$ jest rozbieżny do $+\infty$ wtedy i tylko wtedy, gdy ciąg $b n = - a n$ jest rozbieżny do $-\infty$.

Wskazówka:

Z zadania wynika, że ciągi rozbieżne do nieskończoności "chodzą parami" - każdemu ciągowi rozbieżnemu do $+\infty$ odpowiada ciąg rozbieżny do $-\infty$, który możemy utworzyć, biorąc wyrazy początkowego ciągu z minusem.

Przykład 4.

Ciąg $j n = ( - 2) n$ nie jest rozbieżny ani do $+\infty$, ani do $-\infty$. Intuicyjnie, ma on wyrazy bardzo małe dla dużych $n$ nieparzystych, i bardzo duże dla dużych $n$ parzystych (zobacz rysunek). Wobec tego nie może spełniać żadnego z warunków z definicji 1.

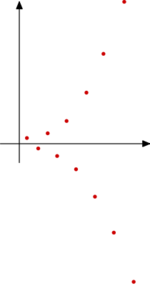
Przykład 5.

Jeśli pewien ciąg jest zbieżny, to jest również ograniczony. Stąd wynika, że ciąg nie może być jednocześnie zbieżny do jakiejś granicy i rozbieżny do nieskończoności.

Przykład 6.

Ciąg $(k n)$ definiujemy następująco: niech $k n = sin n$ dla $n$ podzielnych przez 17, a dla pozostałych wartości $n$ niech $k n = 3 n$ . Ciąg $(k n)$ nie jest rozbieżny do plus nieskończoności, ponieważ ma podciąg ograniczony przez 1, złożony z wyrazów o numerach podzielnych przez 17. To oznacza, że dowolnie daleko w ciągu $(k n)$ są wyrazy mniejsze niż 1, więc dla $K = 1$ nie znajdziemy $n 0$ z definicji rozbieżności do $+\infty$. Ten ciąg nie jest również rozbieżny do $-\infty$, ponieważ dowolnie daleko ma wyrazy dodatnie.

Wyrazy ciągów rozbieżnych do nieskończoności rosną lub maleją nieograniczenie, ale ten proces jest w pewnym sensie pod kontrolą, wynikającą z definicji rozbieżności. Może wobec tego można jakoś kontrolować wyniki operacji na tych ciągach: dodawanie, mnożenie, branie odwrotności...? Szczególne przypadki tego pytania to poniższe zadania. Większość z nich wymaga tylko dobrego zrozumienia definicji rozbieżności do nieskończoności. Warto się dowiedzieć, czy odpowiedzi są zgodne z naszą intuicją - pewnie nie zawsze...

Zadanie 2.

Udowodnić, że jeśli ciąg $(a n)$ jest rozbieżny do nieskończoności i nie ma wyrazów równych 0, to ciąg $b_n = \frac{1}{a_n}$ jest zbieżny do 0.

Zadanie 3.

Udowodnić, że jeśli ciąg $(a n)$ jest zbieżny do 0 i ma wszystkie wyrazy dodatnie, to ciąg $b_n = \frac{1}{a_n}$ jest rozbieżny do $+\infty$.

Zadanie 4.

Udowodnić, że jeśli ciąg $(a n)$ jest zbieżny do 0 i ma wszystkie wyrazy ujemne, to ciąg $b_n = \frac{1}{a_n}$ jest rozbieżny do $-\infty$.

Zadanie 5. (Trochę inny wariant dwóch poprzednich.)

Udowodnić, że jeśli ciąg $(a n)$ jest zbieżny do 0, to ciąg $b_n = \frac{1}{|a_n|}$ jest rozbieżny do $+\infty$, natomiast ciąg $c_n = \frac{1}{-|a_n|}$ jest rozbieżny do $-\infty$.

Zadanie 6.

Udowodnić, że jeśli ciągi $(a n)$ i $(b n)$ są rozbieżne do $+ \infty$, to ich suma $c n = a n + b n$ i iloczyn $d_n = a_n\cdot b_n$ są rozbieżne do $+ \infty$.

Zadanie 7.

Udowodnić, że jeśli ciągi $(a n)$ i $(b n)$ są rozbieżne do $- \infty$, to ich suma $c n = a n + b n$ jest rozbieżna do $-\infty$, a iloczyn $d_n = a_n\cdot b_n$ jest rozbieżny do $+ \infty$.

Zadanie 8.

Udowodnić, że jeśli ciąg $(a n)$ jest rozbieżny do $+\infty$, a ciąg $(b n)$ jest rozbieżny do $- \infty$, to ich iloczyn $d_n = a_n\cdot b_n$ jest rozbieżny do $- \infty$.

Zadanie 9.

Jeśli ciąg $(a n)$ jest rozbieżny do $+\infty$, a ciąg $(b n)$ jest rozbieżny do $- \infty$, to granicy ich sumy $c n = a n + b n$ nie można powiedzieć nic konkretnego. Wskazać przykłady ciągów $(a n)$ i $(b n)$ takie, że

$(c n)$ jest rozbieżny do $+\infty$,
$(c n)$ jest rozbieżny do $-\infty$,
$(c n)$ jest zbieżny do dowolnie wybranej granicy $g$ ,
$(c n)$ nie jest zbieżny ani nie jest rozbieżny do nieskończoności.

Zadanie 10.

Co można powiedzieć o różnicach ciągów rozbieżnych do tej samej nieskończoności?

Zadanie 11.

Jeśli ciąg $(a n)$ jest rozbieżny do nieskończoności, a ciąg $(b n)$ jest zbieżny do 0, to granicy ich iloczynu $d_n = a_n \cdot b_n$ nie można powiedzieć nic konkretnego. Wskazać przykłady ciągów $(a n)$ i $(b n)$ takie, że

$(d n)$ jest rozbieżny do $+\infty$,
$(d n)$ jest rozbieżny do $-\infty$,
$(d n)$ jest zbieżny do dowolnie wybranej granicy $g$ ,
$(d n)$ nie jest zbieżny ani nie jest rozbieżny do nieskończoności.

Theme by Dr. Radut.

Ciągi rozbieżne do nieskończoności

dla autorów