Rozwiązanie zadania 1.9.1:
Sposób I. Co siódma liczba jest podzielna przez 7. Ponieważ 1000 przy dzieleniu przez 7 daje iloraz 142 i resztę 6 (\(1000 = 142 \cdot 7 + 6\) ), więc są 142 takie liczby.
Sposób II. Zbiór liczb od 1 do 1000 włącznie podzielnych przez 7 to zbiór
\(\qquad \{ 7, 14, 21, 28, \ldots , 980, 987, 994 \} = \{ 7n:\, 1 \le n \le 142 \} .\)
Zatem są 142 takie liczby.
Rozwiązanie zadania 1.9.2:
Sposób I. Wśród siedmiu kolejnych liczb jest dokładnie jedna dająca resztę 2 przy dzieleniu przez 7. Liczby od 1 do 994 możemy podzielić na 142 grupy po siedem kolejnych liczb (od 1 do 7, od 8 do 14 itd. aż do grupy liczb od 988 do 994). Zostanie sześć liczb (995, 996, 997, 998, 999 i 1000), wśród których jest jedna liczba dająca resztę 2 przy dzieleniu przez 7 (jest nią 996). Zatem wśród liczb od 1 do 1000 są 143 liczby dające resztę 2 przy dzieleniu przez 7. Natomiast wśród liczb od 1 do 99 takich liczb jest 14: mianowicie jest 14 grup po siedem kolejnych liczb (od 1 do 7, od 8 do 14 itd. aż do grupy liczb od 92 do 98). Zostaje jedna liczba 99, która daje resztę 1 przy dzieleniu przez 7. Odejmując teraz 14 od 143 otrzymujemy odpowiedź: jest 129 takich liczb.
Sposób II. Zbiór liczb, o które chodzi w zadaniu to zbiór
\(\qquad \{ 100, 107, 114, 121, \ldots , 982, 987, 996 \} = \{ 7n+2:\, 14 \le n \le 142 \} .\)
Jest zatem 142 − 13 = 129 takich liczb.
Rozwiązanie zadania 1.9.3:
Sposób I. Mamy 71 grup po 7 kolejnych liczb (od 1 do 7, od 8 do 14 itd. aż do grupy od 491 do 497). W tych grupach jest łącznie \(3 \cdot 71 = 213\) liczb dających reszty 2, 3 lub 4 przy dzieleniu przez 7. W ostatniej grupie liczb (498, 499 i 500) są jeszcze dwie takie liczby (499 daje resztę 2, 500 daje resztę 3). Łącznie mamy zatem 215 takich liczb.
Sposób II. Zbiór liczb dających resztę 2 przy dzieleniu przez 7 to zbiór
\(\qquad \{ 2, 9, 16, 23, \ldots , 492, 499 \} = \{ 7n+2:\, 0 \le n \le 71 \} .\)
Podobnie zbiór liczb dających resztę 3 to zbiór
\(\qquad \{ 3, 10, 17, 24, \ldots , 493, 500 \} = \{ 7n+3:\, 0 \le n \le 71 \}\)
i zbiór liczb dających resztę 4 to zbiór
\(\qquad \{ 4, 11, 18, 25, \ldots , 487, 494 \} = \{ 7n+4:\, 0 \le n \le 70 \} .\)
Mamy więc łącznie 72 + 72 + 71 = 215 takich liczb.
Rozwiązanie zadania 1.9.4: Niech A będzie zbiorem liczb od 1 do 1000 podzielnych przez 3 i niech B będzie zbiorem liczb od 1 do 1000 podzielnych przez 7. Wtedy
\(\qquad |A \setminus B| = |A| - |A \cap B|.\)
Tak jak w jednym z wcześniejszych przykładów, mamy | A | = 333 (bo \(1000 = 333 \cdot 3 + 1\)). Oczywiście \(A \cap B\) jest zbiorem liczb od 1 do 1000 podzielnych przez 21. Zatem \(|A \cap B| = 47\) (bo \(1000 = 47 \cdot 21 + 13\) ). Stąd wynika, że liczb, o które chodzi w zadaniu, jest 333 − 47 = 286 .
Rozwiązanie zadania 1.9.5: Niech A , B i C będą zbiorami liczb od 1 do 500 podzielnych odpowiednio przez 3, 5 i 7. Wtedy
\(\qquad |A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C|.\)
Mamy następnie: | A | = 166 , bo \(500 = 166 \cdot 3 + 2,\) | B | = 100 , bo \(500 = 100 \cdot 5\) , | C | = 71 , bo \(500 = 71 \cdot 7 + 3\) , \(|A \cap B| = 33\) , bo \(500 = 33 \cdot 15 + 5\), \(|A \cap C| = 23\), bo \(500 = 23 \cdot 21 + 17\), \(|B \cap C| = 14\), bo \(500 = 14 \cdot 35 + 10\), \(|A \cap B \cap C| = 4\) , bo \(500 = 4 \cdot 105 + 80\). Stąd dostajemy
\(\qquad |A \cup B \cup C| = 166 + 100 + 71 - 33 - 23 - 14 + 4 = 337 - 70 + 4 = 271.\)
Istnieje zatem 271 liczb, o które chodzi w zadaniu.
Rozwiązanie zadania 1.9.6: W pierwszym rzucie możemy uzyskać jeden z 6 wyników, w drugim też jeden z 6 wyników. Z reguły mnożenia wynika, że łącznie możemy dostać \(6 \cdot 6 = 36\) wyników.
Rozwiązanie zadania 1.9.7: Są 2 ciągi składające się z jednego znaku. Z reguły mnożenia wynika, że istnieją 4 ciągi składające się z dwóch znaków, 8 ciągów składających się z trzech znaków, 16 ciągów długości 4 i wreszcie 32 ciągi długości 5. Łącznie mamy zatem
\(\qquad 2 + 4 + 8 + 16 + 32 = 62\)
takie ciągi.
Rozwiązanie zadania 1.9.8: Na każdym z n miejsc możemy postawić jeden z dwóch znaków: kropkę lub kreskę. Z reguły mnożenia wynika, że mamy 2n ciągów.
Rozwiązanie zadania 1.9.9: Korzystając z wyniku poprzedniego zadania dostajemy
\(\qquad 2 + 4 + 8 + \ldots + 2^ n = 2^{n+1} - 2\)
ciągi.
Rozwiązanie zadania 1.9.10: Na każdym z trzech miejsc możemy napisać jedną z czterech liter. Z reguły mnożenia wynika, że istnieją \(4 \cdot 4 \cdot 4 = 64\) takie wyrazy.
Rozwiązanie zadania 1.9.11: Na pierwszym miejscu może stać jedna z sześciu cyfr. Na każdym z następnych sześciu miejsc może stać jedna z dziesięciu cyfr. Łącznie mamy zatem \(6 \cdot 10^6 = 6\, 000\, 000\) numerów.
Rozwiązanie zadania 1.9.12: Przyjmijmy, że wolno użyć 24 liter. Na każdym z trzech pierwszych miejsc może stać wtedy jedna z 24 liter, na każdym z czterech następnych jedna z 10 cyfr. Łącznie mamy zatem \(24^3 \cdot 10^4 = 138\, 240\, 000\) różnych tablic rejestracyjnych.
Rozwiązanie zadania 1.9.13:
Sposób I. Na ostatnim miejscu może stać jedna z pięciu cyfr nieparzystych. Na pierwszym miejscu może stać jedna z ośmiu cyfr (nie może stać tam ani zero, ani cyfra, którą postawiliśmy na ostatnim miejscu). Na drugim miejscu także może stać jedna z ośmiu cyfr (nie może stać żadna z cyfr wybranych na trzecie i pierwsze miejsce). Z reguły mnożenia wynika, że istnieje \(5 \cdot 8 \cdot 8 = 320\) takich liczb.
Sposób II. W zależności od tego, jakie cyfry stoją na pierwszych dwóch miejscach, mamy cztery przypadki: parzysta, parzysta; pierwsza cyfra parzysta jest jedną z czterech cyfr (oprócz zera), druga też jedną z czterech (oprócz stojącej na pierwszym miejscu), na trzecim miejscu może stać jedna z pięciu cyfr nieparzystych; łącznie mamy \(4 \cdot 4 \cdot 5 = 80\) liczb, parzysta, nieparzysta; pierwsza cyfra jest jedną z czterech cyfr parzystych (oprócz zera), druga cyfra jest jedną z pięciu cyfr nieparzystych, na trzecim miejscu może stać jedna z czterech cyfr nieparzystych (oprócz stojącej na drugim miejscu); łącznie mamy \(4 \cdot 5 \cdot 4 = 80\) liczb, nieparzysta, parzysta; pierwsza cyfra jest jedną z pięciu cyfr nieparzystych, druga cyfra jedną z pięciu cyfr parzystych, na trzecim miejscu może stać jedna z czterech cyfr nieparzystych (oprócz cyfry stojącej na pierwszym miejscu); łącznie mamy \(5 \cdot 5 \cdot 4 = 100\) liczb, nieparzysta, nieparzysta; pierwsza cyfra nieparzysta jest jedną z pięciu cyfr, druga jest jedną z czterech (oprócz stojącej na pierwszym miejscu), na trzecim miejscu może stać jedna z trzech cyfr nieparzystych (oprócz cyfr stojących na pierwszych dwóch miejscach); łącznie mamy \(5 \cdot 4 \cdot 3 = 60\) liczb. Z reguły dodawania wynika, że istnieje 80 + 80 + 100 + 60 = 320 szukanych liczb.
Rozwiązanie zadania 1.9.14:
Sposób I. Istnieje \(9 \cdot 9 \cdot 8 = 648\) liczb trzycyfrowych o różnych cyfrach: na pierwszym miejscu stoi jedna z 9 cyfr, na drugim też jedna z 9 cyfr (oprócz stojącej na pierwszym miejscu), na trzecim jedna z 8 cyfr (oprócz cyfr stojących na pierwszych dwóch miejscach). Wśród tych liczb jest 320 nieparzystych (por. poprzednie zadanie). Pozostaje więc 328 liczb parzystych.
Sposób II. Jeśli na ostatnim miejscu stoi zero, to na pierwszych dwóch miejscach możemy umieścić cyfry na \(9 \cdot 8 = 72\) sposoby (jedna z 9 cyfr na pierwszym miejscu i jedna z 8 na drugim). Jeśli na ostatnim miejscu stoi jedna z czterech różnych od zera cyfr parzystych, to na pierwszych dwóch miejscach możemy umieścić cyfry na \(8 \cdot 8 = 64\) sposoby (jedna z 8 cyfr na pierwszym miejscu – oprócz zera i stojącej na ostatnim miejscu – i jedna z 8 na drugim). Ponieważ są cztery różne od zera cyfry parzyste, więc w tym przypadku mamy \(4 \cdot 64 = 256\) liczb. Z reguły dodawania wynika, że łącznie mamy 72 + 256 = 328 liczb.
Rozwiązanie zadania 1.9.15: Złoty medal dostaje jeden z 8 zawodników, srebrny jeden z 7 zawodników i brązowy jeden z 6 zawodników. Z reguły mnożenia wynika, że mamy \(8 \cdot 7 \cdot 6 = 336\) sposobów przydzielenia medali.
Rozwiązanie zadania 1.9.16: Każda drużyna gra z 15 innymi. W ten sposób każdy mecz policzymy dwukrotnie. Trzeba zatem rozegrać \(\frac{16 \cdot 15 }{ 2} = 120\) meczów.
Rozwiązanie zadania 1.9.17: Niech A i F oznaczają zbiory osób znających odpowiednio język angielski i francuski. Wtedy
\(\qquad |A \cup F| = |A| + |F| - |A \cap F| = 11 + 12 - 3 = 20.\)
Zatem 20 osób zna któryś język. Z tego wynika, że 4 osoby nie znają żadnego z tych dwóch języków.
Rozwiązanie zadania 1.9.18: Niech A i F oznaczają zbiory osób znających odpowiednio język angielski i francuski. Wtedy
\(\qquad |A \cup F| = |A| + |F| - |A \cap F| = 7 + 8 - |A \cap F| = 15 - |A \cap F|.\)
Ponieważ \(|A \cup F| = 17 - 4 = 13\), więc \(|A \cap F| = 2.\) Zatem 2 osoby znają oba języki.
Rozwiązanie zadania 1.9.19:
Sposób I. Niech A , F i N oznaczają zbiory osób znających odpowiednio język angielski, francuski i niemiecki. Wtedy
\(\qquad \begin{array}{ll} |A \cup F \cup N| & = |A| + |F| + |N| - |A \cap F| - |A \cap N| - |F \cap N| + |A \cap F \cap N| = \\ & = 16 + 15 + 19 - 7 - 8 - 10 + 4 = 50 - 25 + 4 = 29. \\ \end{array}\)
Zatem 4 osoby nie znają żadnego języka.
Sposób II. Dane zadania przedstawiamy graficznie:
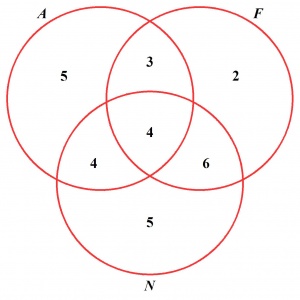
Suma liczb wpisanych we wszystkie składowe jest równa 29, a więc 4 osoby nie znają żadnego języka.
Rozwiązanie zadania 1.9.20:
Sposób I. Niech A , F i N oznaczają zbiory osób znających odpowiednio język angielski, francuski i niemiecki. Wtedy
\(\qquad \begin{array}{ll} |A \cup F \cup N| & = |A| + |F| + |N| - |A \cap F| - |A \cap N| - |F \cap N| + |A \cap F \cap N| = \\ & = 16 + 15 + 17 - 7 - 6 - 9 + |A \cap F \cap N| = 26 + |A \cap F \cap N|. \\ \end{array}\)
Ponieważ \(|A \cup F \cup N| = 33 - 3 = 30,\) więc 4 osoby znają wszystkie trzy języki.
Sposób II. Dane zadania przedstawiamy graficznie (x oznacza liczbę osób znających trzy języki):
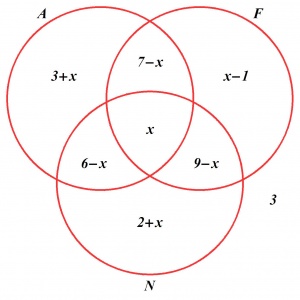
Dodając liczby wpisane we wszystkie składowe, otrzymujemy równanie x + 29 = 33 , a więc 4 osoby znają wszystkie trzy języki.
Rozwiązanie zadania 1.9.21:
Sposób I. Niech A , F i N oznaczają zbiory osób znających odpowiednio język angielski, francuski i niemiecki. Wtedy
\(\qquad \begin{array}{ll} |A \cup F \cup N| & = |A| + |F| + |N| - |A \cap F| - |A \cap N| - |F \cap N| + |A \cap F \cap N| = \\ & = 18 + 17 + 12 - |A \cap F| - 7 - 5 + 2 = 37 - |A \cap F|. \\ \end{array}\)
Ponieważ \(|A \cup F \cup N| = 33 - 6 = 27\) , więc 10 osób zna angielski i francuski.
Sposób II. Dane zadania przedstawiamy graficznie (x oznacza liczbę osób znających angielski i francuski):
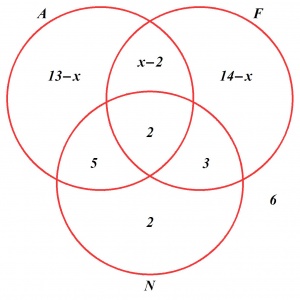
Dodając liczby wpisane we wszystkie składowe, otrzymujemy równanie 43 − x = 33 , a więc 10 osób zna angielski i francuski.
Rozwiązanie zadania 1.9.22:
Sposób I. Niech A , F i N oznaczają zbiory osób znających odpowiednio język angielski, francuski i niemiecki. Wtedy
\(\qquad \begin{array}{ll} |A \cup F \cup N| & = |A| + |F| + |N| - |A \cap F| - |A \cap N| - |F \cap N| + |A \cap F \cap N| = \\ & = 18 + |F| + 15 - 9 - 6 - 5 + 2 = 15 + |F|. \\ \end{array}\)
Ponieważ \(|A \cup F \cup N| = 33 - 2 = 31\) , więc 16 osób zna język francuski.
Sposób II. Dane zadania przedstawiamy graficznie (x oznacza liczbę osób znających język francuski):
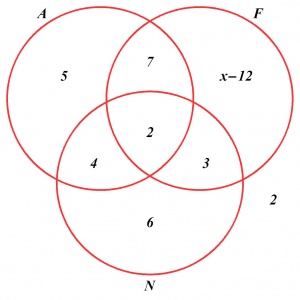
Dodając liczby wpisane we wszystkie składowe, otrzymujemy równanie x + 17 = 33 , a więc 16 osób zna język francuski.
Rozwiązanie zadania 1.9.23: Na pierwszym miejscu można posadzić jedną z 9 osób, na drugim jedną z 8 osób, na trzecim jedną z 7 osób, na czwartym jedną z 6 osób i na piątym jedną z 5 osób. Z reguły mnożenia wynika, że łączna liczba sposobów posadzenia tych osób jest równa \(9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 = 15120\) . Jest to liczba 5-elementowych wariacji bez powtórzeń ze zbioru 9-elementowego.
Rozwiązanie zadania 1.9.24: Każdy sposób uporządkowania tych liczb jest permutacją zbioru 6-elementowego. Mamy zatem 6! = 720 sposobów uporządkowania.
Rozwiązanie zadania 1.9.25: Potraktujmy liczby 1, 2 i 3 jako jeden element zbioru; liczby od 4 do 9 są pozostałymi elementami tego zbioru. Otrzymujemy w ten sposób zbiór 7-elementowy, który można uporządkować na 7! sposobów. Następnie porządkujemy liczby 1, 2 i 3; możemy to zrobić na 3! sposobów. Z reguły mnożenia wynika, że mamy łącznie \(7! \cdot 3! = 5040 \cdot 6 = 30240\) sposobów uporządkowania.
Rozwiązanie zadania 1.9.26: Każdy taki wyraz jest czteroelementową wariacją z powtórzeniami z 32-elementowego zbioru wszystkich liter. Mamy więc \(32^4 = 1\, 048\, 576\) takich wyrazów.
Rozwiązanie zadania 1.9.27: Ponumerujmy osoby liczbami od 1 do 7. Osoba z numerem pierwszym wysiada na jednym z 11 pięter, osoba z numerem drugim na jednym z 10 pozostałych pięter itd. Mamy więc do czynienia z 7-elementowymi wariacjami bez powtórzeń ze zbioru 11-elementowego. Istnieje \(11 \cdot 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 = 1\, 663\, 200\) takich wariacji.
Rozwiązanie zadania 1.9.28: Liczby 2, 3 i 5 możemy uporządkować na 3! sposobów. Pozostałe 4 liczby na 4! sposobów. Z reguły mnożenia wynika, że łącznie mamy \(3! \cdot 4! = 6 \cdot 24 = 144\) sposoby uporządkowania.
Rozwiązanie zadania 1.9.29: Przyjmujemy, że wybieramy wszystkie liczby za jednym razem, a nie po kolei. Inaczej mówiąc, nie jest ważna kolejność wybierania. Jeszcze inaczej, wybieramy 5-elementowy podzbiór zbioru 7-elementowego, czyli 5-elementową kombinację ze zbioru 7-elementowego. Istnieje
\(\qquad {7 \choose 5} = \frac{7! }{ 5! \cdot 2!} = \frac{7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 }{ 5 \cdot 4 \cdot 3 \cdot 2 \cdot 2} = \frac{7 \cdot 6 }{ 2} = 7 \cdot 3 = 21\)
takich 5-elementowych podzbiorów zbioru 7-elementowego.
Rozwiązanie zadania 1.9.30: Ta liczba podzbiorów jest równa
\(\qquad {8 \choose 3} = \frac{8! }{ 3! \cdot 5!} = \frac{8 \cdot 7 \cdot 6 }{ 3!} = 8 \cdot 7 = 56.\)
Rozwiązanie zadania 1.9.31: Możemy to zrobić na
\(\qquad {{24} \choose 5} = \frac{24! }{ 5! \cdot 19!} = \frac{24 \cdot 23 \cdot 22 \cdot 21 \cdot 20 }{ 120} = 23 \cdot 22 \cdot 21 \cdot 4 = 42504\)
sposobów.
Rozwiązanie zadania 1.9.32: Ta liczba sposobów jest równa
\(\qquad \begin{array}{ll} {{52} \choose {13}} & = \frac{52! }{ 13! \cdot 39!} = \frac{52 \cdot 51 \cdot 50 \cdot 49 \cdot 48 \cdot 47 \cdot 46 \cdot 45 \cdot 44 \cdot 43 \cdot 42 \cdot 41 \cdot 40 }{ 13 \cdot 12 \cdot 11 \cdot 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2} = \\ & = 49 \cdot 47 \cdot 46 \cdot 43 \cdot 41 \cdot 40 \cdot 17 \cdot 5 = \\ & = 635\, 013\, 559\, 600. \\ \end{array}\)
Rozwiązanie zadania 1.9.33: Ta liczba sposobów jest równa
\(\qquad {{49} \choose 6} = \frac{49! }{ 6! \cdot 43!} = \frac{49 \cdot 48 \cdot 47 \cdot 46 \cdot 45 \cdot 44 }{ 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2} = 49 \cdot 47 \cdot 46 \cdot 44 \cdot 3 = 13\, 983\, 816.\)
Rozwiązanie zadania 1.9.34: Chłopców wybieramy na jeden z \({{13} \choose 3}\) sposobów, dziewczęta na jeden z \({{12} \choose 2}\) sposobów. Z reguły mnożenia dostajemy
\(\qquad {{13} \choose 3} \cdot {{12} \choose 2} = \frac{13! }{ 3! \cdot 10!} \cdot \frac{12! }{ 2! \cdot 10!} = \frac{13 \cdot 12 \cdot 11 \cdot 12 \cdot 11 }{ 6 \cdot 2} = 13 \cdot 12 \cdot 11 \cdot 11 = 18876\)
sposobów.
Rozwiązanie zadania 1.9.35: Piki wybieramy na jeden z \({{13} \choose 5}\) sposobów, kiery na jeden z \({{13} \choose 2}\) sposobów, kara na jeden z \({{13} \choose 3}\) sposobów i trefle też na jeden z \({{13} \choose 3}\) sposobów. Mamy teraz
\(\qquad\begin{array}{ll} {{13} \choose 5} & = \frac{13! }{ 5! \cdot 8!} = \frac{13 \cdot 12 \cdot 11 \cdot 10 \cdot 9 }{ 120} = 13 \cdot 11 \cdot 9 = 1287, \\ {{13} \choose 2} & = \frac{13! }{ 2! \cdot 11!} = \frac{13 \cdot 12 }{ 2} = 13 \cdot 6 = 78, \\ {{13} \choose 3} & = \frac{13! }{ 3! \cdot 10!} = \frac{13 \cdot 12 \cdot 11 }{ 6} = 13 \cdot 11 \cdot 2 = 286. \\ \end{array}\)
Z reguły mnożenia wynika, że łączna liczba sposobów wyboru kart jest równa
\(\qquad {{13} \choose 5} \cdot {{13} \choose 2} \cdot {{13} \choose 3} \cdot {{13} \choose 3} = 1287 \cdot 78 \cdot 286^2 = 8\, 211\, 173\, 256.\)
Rozwiązanie zadania 1.9.36: Wykonujemy sześć czynności: wybieramy kolor pięciokartowy, wybieramy 5 kart z 13 w tym kolorze, wybieramy kolor dwukartowy, wybieramy 2 karty z 13 w tym kolorze, wybieramy 3 karty z 13 w starszym z pozostałych kolorów, wybieramy 3 karty z 13 w ostatnim kolorze. Czynność pierwszą wykonujemy na jeden z 4 sposobów, drugą na jeden z \({{13} \choose 5}\) sposobów, trzecią na jeden z 3 sposobów (nie możemy wybrać wybranego wcześniej koloru pięciokartowego), czwartą na jeden z \({{13} \choose 2}\) sposobów, każdą z ostatnich dwóch na jeden z \({{13} \choose 3}\) sposobów. Z reguły mnożenia wynika, że łączna liczba sposobów jest równa
\(\qquad 4 \cdot 3 \cdot {{13} \choose 5} \cdot {{13} \choose 2} \cdot {{13} \choose 3} \cdot {{13} \choose 3} = 12 \cdot 8\, 211\, 173\, 256 = 98\, 534\, 079\, 072.\)
Rozwiązanie zadania 1.9.37: Wykonujemy pięć czynności: wybieramy kolor czterokartowy, wybieramy 4 karty z 13 w tym kolorze, wybieramy 3 karty z 13 w najstarszym z pozostałych kolorów, wybieramy 3 karty z 13 w środkowym z pozostałych kolorów, wybieramy 3 karty z 13 w ostatnim kolorze. Czynność pierwszą wykonujemy na jeden z 4 sposobów, drugą na jeden z \({{13} \choose 4}\) sposobów, każdą z pozostałych trzech na jeden z \({{13} \choose 3}\) sposobów. Następnie, obliczamy
\(\qquad {{13} \choose 4} = \frac{13! }{ 4! \cdot 9!} = \frac{13 \cdot 12 \cdot 11 \cdot 10 }{ 24} = 13 \cdot 11 \cdot 5 = 715.\)
Z reguły mnożenia wynika teraz, że łączna liczba sposobów jest równa
\(\qquad 4 \cdot {{13} \choose 4} \cdot {{13} \choose 3} \cdot {{13} \choose 3} \cdot {{13} \choose 3} = 4 \cdot 715 \cdot 286^3 = 66\, 905\, 856\, 160.\)
Rozwiązanie zadania 1.9.38: Wykonujemy sześć czynności: wybieramy kolor trzykartowy, wybieramy 3 karty z 13 w tym kolorze, wybieramy kolor dwukartowy, wybieramy 2 karty z 13 w tym kolorze, wybieramy 4 karty z 13 w starszym z pozostałych kolorów, wybieramy 4 karty z 13 w ostatnim kolorze. Czynność pierwszą wykonujemy na jeden z 4 sposobów, drugą na jeden z \({{13} \choose 3}\) sposobów, trzecią na jeden z 3 sposobów (nie możemy wybrać już wybranego koloru trzykartowego), czwartą na jeden z \({{13} \choose 2}\) sposobów, każdą z ostatnich dwóch na jeden z \({{13} \choose 4}\) sposobów. Z reguły mnożenia wynika, że łączna liczba sposobów jest równa
\(\qquad 4 \cdot 3 \cdot {{13} \choose 3} \cdot {{13} \choose 2} \cdot {{13} \choose 4} \cdot {{13} \choose 4} = 12 \cdot 286 \cdot 78 \cdot 715^2 = 136\, 852\, 887\, 600.\)
Rozwiązanie zadania 1.9.39:
Najpierw obliczymy, na ile sposobów możemy wybrać 10 kart z 52 kart:
\(\qquad \begin{array}{ll} {{52} \choose {10}} & = \frac{52! }{ 10! \cdot 42!} = \frac{52 \cdot 51 \cdot 50 \cdot 49 \cdot 48 \cdot 47 \cdot 46 \cdot 45 \cdot 44 \cdot 43 }{ 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2} = \\ & = 52 \cdot 47 \cdot 43 \cdot 23 \cdot 17 \cdot 11 \cdot 7 \cdot 5 = 15\, 820\, 024\, 220. \\ \end{array}\)
Teraz przystępujemy do rozwiązania zadania. Wykonujemy dwie czynności: wybieramy jednego asa z czterech, a następnie wybieramy 9 kart spośród 48 kart od dwójki do króla. Możemy to zrobić na jeden z \({4 \choose 1} \cdot {{48} \choose 9}\) sposobów. Ta liczba jest równa
\(\qquad \begin{array}{ll} 4 \cdot \frac{48! }{ 9! \cdot 39!} & = 4 \cdot \frac{48 \cdot 47 \cdot 46 \cdot 45 \cdot 44 \cdot 43 \cdot 42 \cdot 41 \cdot 40 }{ 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2} = \\ & = 4 \cdot 47 \cdot 46 \cdot 43 \cdot 41 \cdot 40 \cdot 11 = 6\, 708\, 426\, 560. \\ \end{array}\)
Od liczby wszystkich sposobów wyboru 10 kart odejmujemy liczbę sposobów wyboru kart bez asa:
\(\qquad {{52} \choose {10}} - {{48} \choose {10}}.\)
Mamy teraz
\(\qquad \begin{array}{ll} {{48} \choose {10}} & = \frac{48! }{ 10! \cdot 38!} = \frac{48 \cdot 47 \cdot 46 \cdot 45 \cdot 44 \cdot 43 \cdot 42 \cdot 41 \cdot 40 \cdot 39 }{ 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2} = \\ & = 47 \cdot 46 \cdot 44 \cdot 43 \cdot 41 \cdot 39 = 6\, 540\, 715\, 896. \\ \end{array}\)
Stąd wynika, że liczba wyborów 10 kart z co najmniej jednym asem jest równa
\(\qquad {{52} \choose {10}} - {{48} \choose {10}} = 15\, 820\, 024\, 220 - 6\, 540\, 715\, 896 = 9\, 279\, 308\, 324.\)
Wykonujemy dwie czynności: wybieramy dwa asy z czterech, a następnie wybieramy 8 kart spośród 48 kart od dwójki do króla. Możemy to zrobić na jeden z \({4 \choose 2} \cdot {{48} \choose 8}\) sposobów. Ta liczba jest równa
\(\qquad \begin{array}{ll} 6 \cdot \frac{48! }{ 8! \cdot 40!} & = 6 \cdot \frac{48 \cdot 47 \cdot 46 \cdot 45 \cdot 44 \cdot 43 \cdot 42 \cdot 41 }{ 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2} = \\ & = 6 \cdot 47 \cdot 46 \cdot 43 \cdot 41 \cdot 11 \cdot 9 = 2\, 264\, 093\, 964. \\ \end{array}\)
Od liczby wszystkich sposobów wyboru 10 kart odejmujemy liczbę sposobów wyboru kart bez asa i z dokładnie jednym asem:
\(\qquad \begin{array}{c} {{52} \choose {10}} - {{48} \choose {10}} - {4 \choose 1} \cdot {{48} \choose 9} = \\ = 15\, 820\, 024\, 220 - 6\, 540\, 715\, 896 - 6\, 708\, 426\, 560 = 2\, 570\, 881\, 764. \\ \end{array}\)
Rozwiązanie zadania 1.9.40: Sadzamy na ławce chłopców tak, by zostawić po jednym wolnym miejscu na lewo od nich, między każdymi dwoma i na prawo od nich. Mamy w ten sposób 11 wolnych miejsc. Wybieramy 7 z nich i na tych miejscach sadzamy dziewczęta. Chłopców możemy w ten sposób posadzić na jeden z 10! sposobów. Miejsca dla dziewcząt wybieramy na jeden z \({{11} \choose 7}\) sposobów. Wreszcie sadzamy dziewczęta na jeden z 7! sposobów. Z reguły mnożenia wynika, że lączna liczba sposobów posadzenia chłopców i dziewcząt jest równa
\(\qquad 10! \cdot {{11} \choose 7} \cdot 7! = 10! \cdot \frac{11! }{ 7! \cdot 4!} \cdot 7! = \frac{10! \cdot 11! }{ 4!} = 6\, 035\, 420\, 160\, 000.\)
Rozwiązanie zadania 1.9.41:
Sposób I. Pierwszy zbiór wybieramy na jeden z \({6 \choose 2}\) sposobów, drugi na jeden z \({4 \choose 2}\) sposobów. Trzeci zbiór jest złożony z ostatnich dwóch elementów. Ponieważ nie uwzględniamy kolejności zbiorów, więc otrzymany wynik należy podzielić przez 3! . Liczba takich podziałów jest więc równa
\(\qquad \frac{1 }{ 3!} \cdot {6 \choose 2} \cdot {4 \choose 2} = \frac{1 }{ 3!} \cdot \frac{6! }{ 2! \cdot 4!} \cdot \frac{4! }{ 2! \cdot 2!} = \frac{6! }{ 3! \cdot (2!)^3} = 15.\)
Sposób II. Ustawiamy 6 elementów naszego zbioru w ciąg. Pierwsze dwa elementy tworzą pierwszy zbiór, trzeci i czwarty tworzą drugi zbiór, ostatnie dwa tworzą trzeci zbiór. Ten sam podział otrzymamy zamieniając dowolnie elementy w wybranych parach (w każdej parze na 2! sposobów) oraz zamieniając pary między sobą (na 3! sposobów). Łączna liczba podziałów jest więc równa
\(\qquad \frac{6! }{ 3! \cdot (2!)^3} = 15.\)
Rozwiązanie zadania 1.9.42: Zastosujemy sposób II z poprzedniego zadania. Porządkujemy wszystkie elementy zbioru mn-elementowego na jeden z (mn)! sposobów. Następnie dzielimy zbiór na n grup m -elementowych: pierwsze m elementów, następne m elementów itd. Ten sam podział otrzymamy porządkując dowolnie każdą grupę (w każdej grupie mamy m! porządków; z reguły mnożenia wynika, że takich uporządkowań jest (m!)n ) oraz zamieniając dowolnie te grupy (na jeden z n! sposobów). Łączna liczba podziałów jest więc równa
\(\qquad \frac{(mn)!}{(m!)^ n \cdot n!}.\)
Rozwiązanie zadania 1.9.43: Podstawiając m = n w poprzednim zadaniu, dostajemy wzór na liczbę podziałów zbioru n2 -elementowego na n podzbiorów n-elementowych. Ta liczba jest równa
\(\qquad \frac{(n^2)! }{ n! \cdot (n!)^ n} = \frac{(n^2)! }{ (n!)^{n+1}}.\)
Ponieważ liczba podziałów jest liczbą całkowitą, więc liczba (n2)! dzieli się bez reszty przez (n!)n + 1 .
Rozwiązanie zadania 1.9.44: Zliczamy na dwa sposoby podzbiory zbioru n -elementowego. Każdy taki podzbiór jest albo zbiorem zeroelementowym, albo zbiorem jednoelementowym, albo zbiorem dwuelementowym itd. Ogólnie mówiąc, jest zbiorem k-elementowym dla pewnej liczby k takiej, że \(0 \le k \le n\) . Z reguły dodawania wynika, że liczba tych podzbiorów jest równa
\(\qquad {n \choose 0} + {n \choose 1} +\ldots + {n \choose {n-1}} + {n \choose n}.\)
Z drugiej strony, wiemy, że ta liczba jest równa 2n . Stąd wynika wzór
\(\qquad {n \choose 0} + {n \choose 1} +\ldots + {n \choose {n-1}} + {n \choose n} = 2^ n.\)
Rozwiązanie zadania 1.9.45: Mamy daną grupę n osób. Wybieramy spośród nich m osób, które pojadą na wycieczkę. Następnie spośród wybranych osób wybieramy jeszcze k osób, które prosimy o wzięcie prowiantu. Liczbę takich wyborów zliczamy na dwa sposoby: Osoby, które pojadą na wycieczkę, wybieramy na jeden z \({n \choose m}\) sposobów. Niezależnie od tego, które osoby zostaną wybrane, wyboru k osób spośród nich możemy dokonać na \({m \choose k}\) sposobów. Z reguły mnożenia wynika, że łącznie mamy
\(\qquad {n \choose m} \cdot {m \choose k}\)
sposobów wyboru. Możemy najpierw wybrać k osób, które zajmą się prowiantem (na jeden z \({n \choose k}\) sposobów). Następnie uzupełniamy skład wycieczki: spośród pozostałych n − k osób dobieramy m − k osób: możemy dokonać tego na jeden z \({{n-k} \choose {m-k}}\) sposobów. Z reguły mnożenia wynika, że mamy łącznie
\(\qquad {n \choose k} \cdot {{n-k} \choose {m-k}}\)
sposobów wyboru.
Ponieważ liczba sposobów wyboru nie zależy od tego, w jaki sposób je zliczamy, więc
\(\qquad {n \choose m}{m \choose k} = {n \choose k}{{n-k} \choose {m-k}}.\)
Rozwiązanie zadania 1.9.46: Powtórzymy rozwiązanie zadania 1.8.7. z rozdziału 8. Mamy daną grupę n kobiet i m mężczyzn. Z tej grupy mamy wybrać k osób. Na ile sposobów możemy to zrobić? Oczywiście liczba sposobów jest równa \({{m+n} \choose k}\) , bo tyle jest k-elementowych podzbiorów zbioru (m + n) -elementowego. Popatrzmy teraz na to zadanie inaczej. Zapytajmy najpierw, na ile sposobów można wybrać grupę złożoną z l kobiet i k − l mężczyzn. Oczywiście kobiety można wybrać na \({n \choose l}\) sposobów, mężczyzn zaś na \({m \choose {k-l}}\) sposobów. Z reguły mnożenia wynika, że obu wyborów razem można dokonać na \({n \choose l} \cdot {m \choose {k-l}}\) sposobów. Teraz zauważmy, że w naszej grupie wybranych k osób może być 0 kobiet lub 1 kobieta lub 2 kobiety lub \(\ldots\) k kobiet. Z reguły dodawania wynika, że grupę k osób można wybrać na
\(\qquad {n \choose 0} \cdot {m \choose k} + {n \choose 1} \cdot {m \choose {k-1}} +\ldots + {n \choose {k-1}} \cdot {m \choose 1} + {n \choose k} \cdot {m \choose 0}\)
sposobów. Tę samą liczbę sposobów obliczyliśmy dwiema metodami, więc wyniki muszą być równe. Stąd otrzymujemy równość
\(\qquad {n \choose 0} \cdot {m \choose k} + {n \choose 1} \cdot {m \choose {k-1}} +\ldots + {n \choose {k-1}} \cdot {m \choose 1} + {n \choose k} \cdot {m \choose 0} = {{m+n} \choose k}.\)
Rozwiązanie zadania 1.9.47: Mamy grupę n osób. Wybieramy pewną liczbę osób, które pojadą na wycieczkę i wybieramy kierownika wycieczki (spośród osób jadących na wycieczkę). Policzymy dwiema metodami liczbę sposobów takiego wyboru. Najpierw ustalamy liczbę k osób, które pojadą na wycieczkę (oczywiście \(k \ge 1\) , bo co najmniej jedna osoba – kierownik – musi pojechać). Następnie dla danej liczby k wybieramy k osób (na jeden z \({n \choose k}\) sposobów) i kierownika (niezależnie od tego, które osoby zostaną wybrane, na jeden z k sposobów). Z reguły mnożenia wynika, że dla danego k mamy \(k \cdot {n \choose k}\) sposobów wyboru. Ponieważ k może przybierać dowolne wartości spośród liczb od 1 do n , więc z reguły dodawania wynika, że liczba sposobów wyboru jest równa
\(\qquad 1 \cdot {n \choose 1} + 2 \cdot {n \choose 2} +\ldots + (n-1) \cdot {n \choose {n-1}} + n \cdot {n \choose n}.\)
Możemy najpierw wybrać kierownika (na jeden z n sposobów). Następnie spośród pozostałych n − 1 osób możemy dobrać pewną liczbę osób, które wyślemy na wycieczkę wraz z wybranym kierownikiem. Ponieważ, jak wiemy, zbiór (n − 1) -elementowy ma 2n − 1 podzbiorów, więc z reguły mnożenia wynika, że łączna liczba sposobów wyboru jest równa \(n \cdot 2^{n-1}\) . Liczba sposobów wyboru nie zależy od metody zliczania, więc mamy równość
\(\qquad 1 \cdot {n \choose 1} + 2 \cdot {n \choose 2} +\ldots + (n-1) \cdot {n \choose {n-1}} + n \cdot {n \choose n} = n \cdot 2^{n-1}.\)
Rozwiązanie zadania 1.9.48: Mamy grupę n osób. Wybieramy pewną liczbę osób, które pojadą na wycieczkę i wybieramy kierownika wycieczki oraz jego zastępcę (spośród osób jadących na wycieczkę). Policzymy dwiema metodami liczbę sposobów takiego wyboru. Najpierw ustalamy liczbę k osób, które pojadą na wycieczkę (oczywiście \(k \ge 2\) , bo co najmniej dwie osoby – kierownik i jego zastępca – muszą pojechać). Następnie dla danej liczby k wybieramy k osób (na jeden z \({n \choose k}\) sposobów), kierownika (niezależnie od tego, które osoby zostaną wybrane, na jeden z k sposobów) i jego zastępcę (niezależnie od tego, które osoby zostaną wybrane na wycieczkę i kto zostanie wybrany kierownikiem, na jeden z k − 1 sposobów). Z reguły mnożenia wynika, że dla danego k mamy \(k \cdot (k-1) \cdot {n \choose k}\) sposobów wyboru. Ponieważ k może przybierać dowolne wartości spośród liczb od 2 do n , więc z reguły dodawania wynika, że liczba sposobów wyboru jest równa
\(\qquad 2 \cdot 1 \cdot {n \choose 2} + 3 \cdot 2 \cdot {n \choose 3} +\ldots + (n-1) \cdot (n-2) \cdot {n \choose {n-1}} + n \cdot (n-1) \cdot {n \choose n}.\)
Możemy najpierw wybrać kierownika (na jeden z n sposobów) oraz jego zastępcę (niezależnie od tego, kto zostanie wybrany kierownikiem, na jeden z n − 1 sposobów). Następnie spośród pozostałych n − 2 osób możemy dobrać pewną liczbę osób, które wyślemy na wycieczkę wraz z wybranym kierownikiem i jego zastępcą. Ponieważ zbiór (n − 2)-elementowy ma 2n − 2 podzbiorów, więc z reguły mnożenia wynika, że łączna liczba sposobów takiego wyboru jest równa \(n \cdot (n-1) \cdot 2^{n-2}\) . Liczba sposobów wyboru nie zależy od metody zliczania, więc mamy równość
\(\qquad 2 \cdot 1 \cdot {n \choose 2} + 3 \cdot 2 \cdot {n \choose 3} +\ldots + (n-1) \cdot (n-2) \cdot {n \choose {n-1}} + n \cdot (n-1) \cdot {n \choose n} = n(n-1)2^{n-2}.\)
Rozwiązanie zadania 1.9.49: Mamy grupę n osób. Wybieramy pewną liczbę osób, które pojadą na wycieczkę i wybieramy kierownika wycieczki oraz skarbnika (spośród osób jadących na wycieczkę). Zakładamy, że skarbnikiem może być dowolny uczestnik wycieczki, również kierownik. Policzymy dwiema metodami liczbę sposobów takiego wyboru. Najpierw ustalamy liczbę k osób, które pojadą na wycieczkę (oczywiście \(k \ge 1\) , bo co najmniej jedna osoba – kierownik – musi pojechać). Następnie dla danej liczby k wybieramy k osób (na jeden z \({n \choose k}\) sposobów), kierownika (niezależnie od tego, które osoby zostaną wybrane, na jeden z k sposobów) i skarbnika (niezależnie od tego, które osoby zostaną wybrane na wycieczkę i kto zostanie wybrany kierownikiem, na jeden z k sposobów). Z reguły mnożenia wynika, że dla danego k mamy \(k^2 \cdot {n \choose k}\) sposobów wyboru. Ponieważ k może przybierać dowolne wartości spośród liczb od 2 do n , więc z reguły dodawania wynika, że liczba sposobów wyboru jest równa
\(\qquad 1^2 \cdot {n \choose 1} + 2^2 \cdot {n \choose 2} +\ldots + (n-1)^2 \cdot {n \choose {n-1}} + n^2 \cdot {n \choose n}.\)
Możemy najpierw wybrać kierownika (na jeden z n sposobów) oraz skarbnika. Teraz mamy dwa przypadki.
(1) Jeśli skarbnikiem zostanie kierownik wycieczki, to pozostałych uczestników wycieczki dobieramy spośród n − 1 osób (na jeden z 2n − 1 sposobów).
(2) Jeśli zaś skarbnikiem jest inna osoba, to pozostałych uczestników musimy dobrać spośród n − 2 osób (na jeden z 2n − 2 sposobów).
Korzystając z reguł mnożenia i dodawania, stwierdzamy, że łączna liczba sposobów takiego wyboru jest równa
\(\qquad n \cdot 2^{n-1} + n \cdot (n-1) \cdot 2^{n-2} = n \cdot 2^{n-2} \cdot (2 + n - 1) = n \cdot (n+1) \cdot 2^{n-2}.\)
Liczba sposobów wyboru nie zależy od metody zliczania, więc mamy równość
\(\qquad 1^2 \cdot {n \choose 1} + 2^2 \cdot {n \choose 2} +\ldots + (n-1)^2 \cdot {n \choose {n-1}} + n^2 \cdot {n \choose n} = n(n+1) \cdot 2^{n-2}.\)
Rozwiązanie zadania 1.9.50: Ze zbioru liczb \(\{ 1,2,\ldots ,n,n+1\}\) wybieramy m + 1 liczb. Na ile sposobów możemy to zrobić? Liczbę sposobów wyboru obliczamy na dwa sposoby. Oczywiście ta liczba sposobów jest równa \({{n+1} \choose {m+1}}\) , bo tyle jest (m + 1)-elementowych podzbiorów zbioru (n + 1)-elementowego. Zauważmy, że największą wybraną liczbą jest jedna z liczb
\(\qquad m+1, m+2, m+3, \ldots , n, n+1.\)
Jeśli największą wybraną liczbą jest k + 1 (gdzie \(m \le k \le n\) ), to mniejsze od niej zostały wybrane ze zbioru \(\{ 1,2,3,\ldots ,k\}\). Mamy więc wtedy \({k \choose m}\) sposobów wyboru (spośród k liczb wybieramy m liczb, bo największa, k + 1, jest już wybrana). Z reguły dodawania wynika, że liczba sposobów takiego wyboru jest zatem równa
\(\qquad {m \choose m} + {{m+1} \choose m} +\ldots + {{n-1} \choose m} + {n \choose m}.\)
Liczba sposobów wyboru nie zależy od metody zliczania, więc mamy równość
\(\qquad {m \choose m} + {{m+1} \choose m} +\ldots + {{n-1} \choose m} + {n \choose m} = {{n+1} \choose {m+1}}.\)
