Zbiór jest jednoznacznie określony przez swoje elementy. Czyli dwa zbiory są równe tylko wtedy gdy mają takie same elementy (kolejność nie ma znaczenia). Na przykład {0,1,{7,8}} = {1,{8,7},0}, bo oba zbiory zawierają liczby 0,1 i zbiór zawierający 7,8.
Aby powiedzieć, że zbiór zawiera w sobie jakiś obiekt, używa się znaczku \(\in\). Na przykład \(7\in\{4,5,7\}\), czyli 7 jest elementem zbioru {4,5,7}. Może być odwrotnie, na przykład \(5\notin\{1,2\}\), czyli 5 nie jest elementem zbioru {1,2}. Oczywiście nic nie jest elementem zbioru pustego \(\emptyset\). Bardziej złożony przykład, to \(\{6,3\}\in\{1,2,\{3,6\}\}\).
Jest bardzo ważne, żeby zrozumieć że \(\{1,2\}\notin\{1,2,\{1\},\{2\},\{1,2,3\}\}\), bo jakkolwiek dany zbiór zawiera liczby 1,2, zbiory {1},{2}, a nawet zbiór {1,2,3}, to samego zbioru {1,2} nie zawiera!
Elementy zbiorów oznacza się małymi literami, często takimi jak odpowiedni zbiór, na przykład \(a\in A\).
Intuicje
Generalnie o zbiorach można myśleć o zbiornikach (koszykach) w których znajdują się jakieś obiekty (np. owoce). Podejście takie pozwala sobie łatwo wyobrazić różne własności zbiorów, jednak ma też swoje wady. Chodzi mianowicie o warunek, by każdy element występował w danym zbiorze co najwyżej raz. W rzeczywistości, zazwyczaj tego typu założenie nie jest spełnione, na przykład w koszyku może znajdować się 5 takich samych jabłek.
Jeśli jednak będziemy dbać o to, by sklejać ze sobą takie same obiekty, intuicje z życia codziennego mogą być pomocne. Na przykład zbiór wszystkich drzew na świecie dzieli się na dwa podzbiory - drzewa iglaste i drzewa liściaste. Co więcej, te podzbiory są rozłączne - żadne drzewo nie jest jednocześnie iglaste i liściaste. No i w sumie te dwa zbiory wyczerpują całość, bo każde drzewo jest albo iglaste, albo liściaste.
Oprócz intuicji z życia codziennego, przydatne są czasami obrazki. Chodzi o tzw. diagramy Venna. Diagram taki składa się z kształtów (zazwyczaj kółek) z których każdy prezentuje jeden zbiór. Przykład takiego diagramu, to:
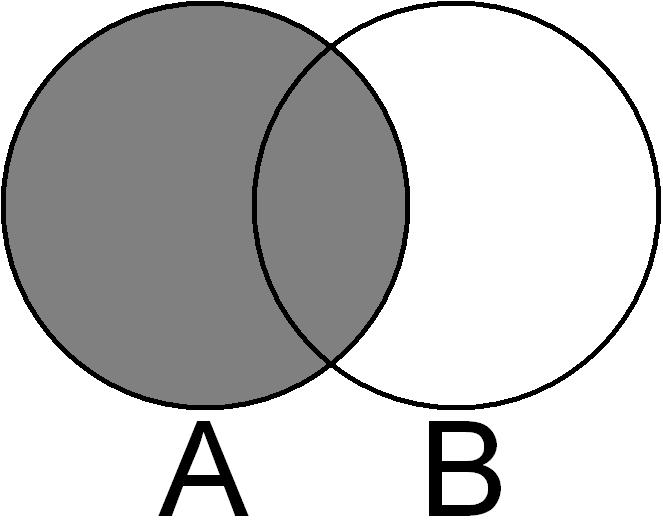
Obrazek ten prezentuje dwa kółka: jedno odpowiada zbiorowi A, a drugie zbiorowi B. Zaznaczony na szaro obszar to zbiór A. Obrazek jest bardzo prosty, ale pokazuje ogólną sytuację:
- na obrazku są miejsca leżące wewnątrz zbioru A i poza zbiorem B,
- są miejsca leżące w obu zbiorach,
- są miejsca leżące w B i nie w A,
- są wreszcie miejsca które nie są w żadnym ze zbiorów - zewnętrzna część obrazka.
Jako proste ćwiczenie warto rozpoznać, który obszar na obrazku odpowiada któremu z powyższych punktów.
Zaznaczony na szaro obszar, czyli zbiór A, to miejsca pierwszego i drugiego typu spośród powyższej listy.
Liczność
Można liczyć ile elementów mają zbiory. Dla danego zbioru A, liczbę jego elementów oznaczamy | A | . Na przykład | {1,2,3} | = 3, a \(|\emptyset|=0\). Należy pamiętać, że | {{1,2,3,4,5}} | = 1, bo ten zbiór ma jeden element - inny zbiór. Czasami ta liczba jest nieskończona (ozn. \(\infty\)), na przykład zbiór liczb naturalnych \(\mathbb N\) ma nieskończenie wiele elementów, można to zapisać \(|\mathbb N|=\infty\).
Liczbę elementów zbioru nazywamy jego mocą. Na przykład zbiór {0,1,} ma moc 2. Oczywiście moc zbioru nie może być ujemna i nie może być ułamkiem - nie ma zbioru mocy \(7\frac{13}{5}\). Jeśli moc zbioru wynosi 0, oznacza że jest to zbiór pusty, czyli \(\emptyset\).
