Dla dowolnego obiektu x, można stworzyć zbiór, który składa się tylko z tego jednego obiektu. Zbiór taki to po prostu {x}, jego moc jest zawsze równa 1. Zbiór taki, który ma tylko jeden element, nazywamy singletonem tego elementu. Na przykład {7}, to singleton 7. Oczywiście singleton x, to co innego niż x. W szczególności \(\{\emptyset\}\neq\emptyset\), bo pierwszy z nich ma jeden element: zbiór pusty, a drugi nie ma żadnych elementów.
Suma
Sumą dwóch zbiorów nazywamy zbiór składający się z tych elementów, które leżą w przynajmniej jednym ze zbiorów. Jeśli jakiś element jest w obu zbiorach, to do sumy wchodzi tylko raz! Sumę zbiorów A,B oznaczamy \(A\cup B\). Na przykład \(\{0,1\}\cup\{1,2\}=\{0,1,2\}\).
Odpowiedni diagram Venna jest następujący:
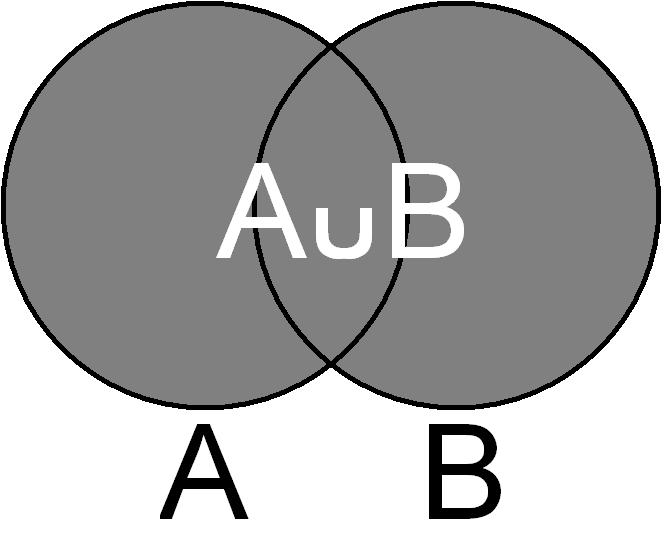
Warto zrozumieć, że elementy sumy zbiorów są trzech typów:
- te elementy, które są w pierwszym zbiorze i nie są w drugim,
- te elementy, które są w drugim zbiorze i nie są w pierwszym,
- elementy obecne w obu zbiorach jednocześnie.
Oczywiście, dla dowolnego zbioru A, zachodzi równość \(A\cup\emptyset=A\), bo zbiór \(\emptyset\) jest pusty, więc nie dorzuca ze swojej strony żadnych elementów do sumy. Podobnie \(A\cup A=A\).
Przecięcie
Druga podstawowa operacja, to przecięcie (nazywane też częścią wspólną). Przecięcie zbiorów A,B oznaczamy \(A\cap B\), zawiera ono te elementy które są obecne zarówno w A jak i w B. Na przykład \(\{0,1\}\cap\{1,2\}=\{1\}\). Oczywiście przecięcie zawiera każdy element raz.
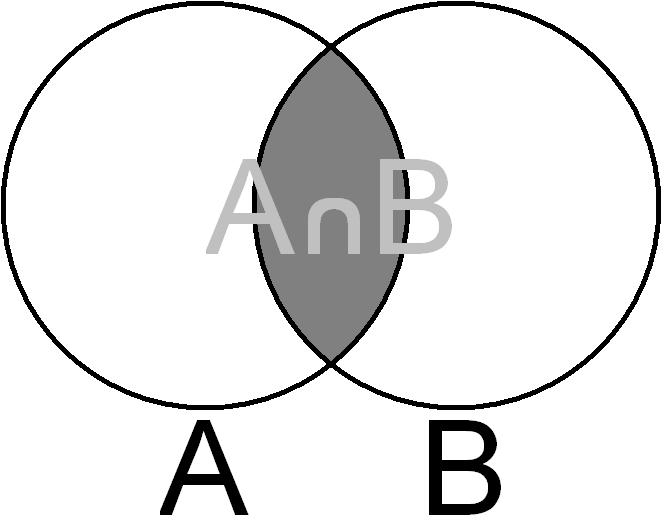
Dla dowolnego zbioru A zachodzi \(A\cap \emptyset=\emptyset\), bo nie ma żadnego elementu, który by należał do \(\emptyset\). Podobnie \(A\cap A=A\).
Różnica
Kolejna operacja to różnica zbiorów. Dla danych A,B, ich różnicę oznaczamy \(A\setminus B\), zawiera ona elementy należące do A, ale nie należące do B. Ważne jest, że B może zawierać jakieś elementy których nie ma w A, nie są one wtedy liczone ujemnie. Czyli \(\{0,1\}\setminus\{1,2\}=\{0\}\).
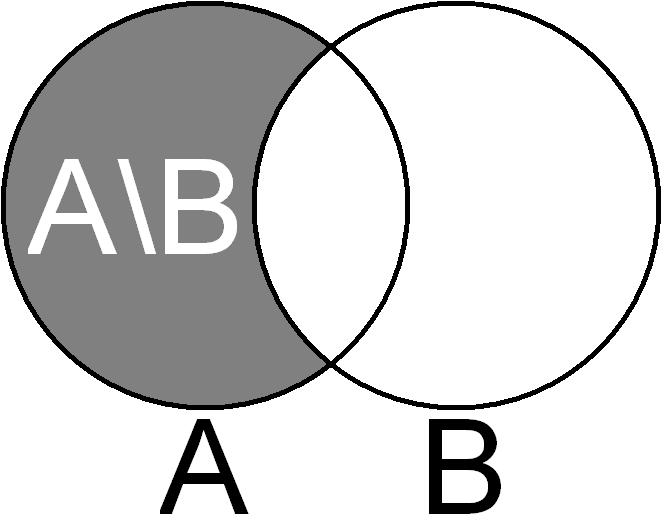
Gdy odejmujemy dwie liczby, pierwsza z nich maleje dokładnie o tyle, jak duża jest druga liczba. W przypadku zbiorów tak nie jest, w powyższym przykładzie odejmujemy dwa zbiory z których każdy ma dwa elementy i dostajemy zbiór zawierający jeden element. Rzecz w tym, że drugi z odejmowanych zbiorów może mieć dużo dodatkowych elementów, których nie ma w pierwszym, więc nie mają znaczenia.
Oto kilka równości, zachodzących niezależnie od zbiorów A,B:
- \(A\setminus \emptyset = A\),
- \(\emptyset\setminus A= \emptyset\), w szczególności \(\emptyset\setminus \emptyset= \emptyset\),
- \((A\setminus B)\cap B=\emptyset\), bo w różnicy \(A\setminus B\), nie ma żadnych elementów B,
- \((A\setminus B)\cap (B\setminus A)=\emptyset\), bo pierwszy ze zbiorów nie zawiera żadnego elementu B, a drugi składa się tylko z pewnych elementów B, więc ich przecięcie jest puste.
Iloczyn
Iloczyn kartezjański to pierwsza nietrywialna operacja na zbiorach. Chodzi o to, że czasami przydatne jest operować na parach obiektów. Na przykład punkty na płaszczyźnie można traktować jako pary liczb rzeczywistych - współrzędna X i współrzędna Y. Parę złożoną z elementów x,y oznaczamy (x,y). W takiej parze, pierwszy człon nazywamy pierwszą współrzędną, a drugi człon drugą współrzędną. Kolejność współrzędnych ma znaczenie, tzn. (o ile \(x\neq y\)) \((x,y)\neq (y,x)\), bo różnią się na pierwszej współrzędnej (na drugiej zresztą też).
Iloczyn kartezjański nazywany jest czasami produktem dwóch zbiorów. Pochodzi to od angielskiego słowa product.
Dla danych zbiorów A,B ich iloczyn kartezjański oznaczamy \(A\times B\). Składa się on ze wszystkich możliwych par (a,b), gdzie \(a\in A\) i \(b\in B\). Na przykład \(\{0,1\}\times\{1,2\}=\{(0,1),(0,2),(1,1), (1,2)\}\). Nie ma znaczenia, czy zbiory które mnożymy mają jakieś wspólne elementy, czy nie, bo elementy lewego zbioru zawsze są na pierwszej współrzędnej, a prawego na drugiej - nie mieszają się ze sobą.
Podstawowy i główny przykład to płaszczyzna, którą możemy traktować jako iloczyn \(\mathbb R\times \mathbb R\), czyli zbiór par liczb rzeczywistych. Ale możemy na przykład rozważać zbiór \(\mathbb R\times\mathbb N\), czyli zbiór par, gdzie pierwsza współrzędna to liczba rzeczywista, a druga to liczba naturalna. Do tego zbioru należy na przykład (π,7), ale nie należy (7,π).
Selekcja
Chyba najciekawszą operacją jaką można dokonać na zbiorach, jest 'selekcja'. Chodzi o to, by z danego zbioru wybrać tylko te elementy, które mają pewną określoną własność.
Załóżmy, że dany jest dowolny zbiór A i dowolna formuła rachunku predykatów, zależna od a. Formułę tą oznaczamy \(\varphi(a)\). Wtedy dobrze określony jest zbiór \(\{a\in A:\varphi(a)\}\), czyli zbiór tych elementów \(a\in A\), które spełniają formułę \(\varphi(a)\).
Oto kilka przykładów:
- Przykład trywialny: \(\{a\in\{0,1,2,3\}:a>1\}=\{2,3\}\). Ze zbioru {0,1,2,3}, wybieramy wszystkie te elementy, które są większe niż 1. Dostajemy w ten sposób zbiór {2,3}.
- Weźmy za zbiór A liczby naturalne \(\mathbb N\), a formuła niech będzie następująca: \(\varphi(n)=\exists_{m\in\mathbb N} 2m=n\). Formuła ta mówi, że istnieje liczba, której dwukrotność jest równa n, czyli że n jest liczbą parzystą. Wtedy zbiór \(\{n\in \mathbb N: \exists_{m\in\mathbb N} 2m=n\}\), to dokładnie zbiór parzystych liczb naturalnych.
- Rozważmy \(\{(a,b)\in \mathbb R\times\mathbb N: b=7\}\). Jest to zbiór tych par (liczba rzeczywista, liczba naturalna), że druga z liczb w parze jest równa 7. Czyli jest to zbiór par postaci (x,7), po wszystkich możliwych \(x\in\mathbb R\).
Korzystając z singletona i iloczynu, można napisać równość: \(\{(a,b)\in \mathbb R\times\mathbb N: b=7\}=\mathbb R\times \{7\}\), która mówi że zbiór par gdzie druga współrzędna wynosi 7 to jest iloczyn kartezjański wszystkich liczb rzeczywistych i zbioru składającego się z samej liczby 7.
Zbiór potęgowy
Najbardziej skomplikowaną operacją jaką można wykonać na zbiorach jest tzw. zbiór potęgowy. Można mianowicie, dla danego zbioru (na przykład {1,2}), spytać o wszystkie możliwe zbiory składające się z jego elementów. W tym przykładzie, są to zbiory \(\emptyset,\{1\},\{2\},\{1,2\}\). Zbiór zawierający wszystkie zbiory złożone z elementów danego zbioru A, nazywamy zbiorem potęgowym A i oznaczamy P(A). Czyli w powyższym przykładzie \(P(\{1,2\})=\{\emptyset,\{1\},\{2\},\{1,2\}\}\).
Do zbioru potęgowego wchodzą tylko elementy danego zbioru. Nie wchodzimy w ich głąb. Więc na przykład \(P(\{1,\{2,3\}\})=\{\emptyset, \{1\}, \{\{2,3\}\},\{1,\{2,3\}\}\}\). Dodatkowo trzeba pamiętać, że \(P(\emptyset)=\{\emptyset\}\neq \emptyset\), czyli zbiór potęgowy zbioru pustego to zbiór składający się ze zbioru pustego, czyli singleton zbioru pustego.
Porównywanie
Zbiory można ze sobą porównywać. I nie chodzi tu wcale o porównanie ich mocy (czyli liczby elementów), tylko o coś nieco subtelniejszego. Powiemy, że zbiór A jest podzbiorem zbioru B (ozn. \(A\subseteq B\)), jeśli każdy element \(a\in A\) jest też elementem B. Na przykład \(\{1,2\}\subseteq \{0,1,2\}\), ale nie zachodzi \(\{3,4\}\subseteq \{1,2,3\}\), bo 4 jest elementem pierwszego zbioru i nie jest drugiego.
Oczywiście, niezależnie od zbioru A, zawsze zachodzi \(\emptyset\subseteq A\). Dodatkowo, jeśli \(A\subseteq B\) i \(B\subseteq C\), to też \(A\subseteq C\). I oczywiście \(A\subseteq A\). Więc na znaczek \(\subseteq\) można patrzeć trochę analogicznie do znaczka \(\leq\) pomiędzy liczbami.
Należy jednak nieco uważać, bo dla zbiorów A = {0,1} i B = {1,2}, nie zachodzi ani \(A\subseteq B\), ani \(B\subseteq A\). O takich zbiorach mówimy, że są nieporównywalne.
Łatwo sprawdzić następujące własności:
- \(A\subseteq A\cup B\),
- \(A\cap B\subseteq A\),
- \(A\setminus B\subseteq A\),
- \(\{a\in A:\varphi(a)\}\subseteq A\), niezależnie od formuły \(\varphi\).
Znaczek \(\subseteq\) można oczywiście pisać też w drugą stronę, czyli \(A\supseteq B\), oznacza to samo co \(B\subseteq A\). Dodatkowo zauważmy, że jeśli \(A\subseteq B\) i \(A\supseteq B\), to A = B. Czyli jeśli każdy element A jest też elementem B i odwrotnie, to znaczy, że zbiory A,B zawierają te same elementy. To jest bardzo ważna własność!
