Przy rozwiązywaniu zadań mamy do dyspozycji dwa warunki równoważne temu, że czworokąt ABCD jest wpisany w okrąg:
(1) sumy naprzeciwległych kątów są równe 180 stopni (Twierdzenie 1),
(2) kąty ACB i ADB mają tę samą miarę (Twierdzenie 2).
Często celem jest obliczenie miary pewnych kątów w czworokącie lub innej figurze wpisanej w okrąg. Wtedy, w zależności od danych zadania, przydaje się warunek (1) lub (2), a w wielu problemach trzeba wykorzystać oba twierdzenia.
Jeśli natomiast chcemy wykazać, że pewien czworokąt jest wpisany w okrąg, to warto pamiętać, że warunek (1) wystarczy sprawdzić dla jednej pary naprzeciwległych kątów, bo jeśli kąty z jednej pary dają w sumie 180 stopni, to kąty z drugiej pary sumują się do 360 - 180 = 180 stopni. Warunek (2) oczywiście możemy sprawdzić dla dowolnej pary kątów opartych na którymś boku czworokąta, o wierzchołkach niebędących końcami tego boku (czyli w czworokącie ABCD możemy sprawdzać go dla par ACB i ADB, BAC i BDC, CAD i CBD oraz DBA i DCA).
Na początek nietrudne zadanie, które pokazuje, jak wykorzystać warunek (1) do obliczeń miar kątów.
Przykład 1 (Zadanie 1)
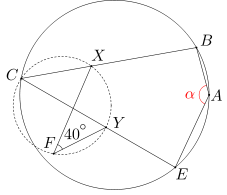
Punkty A, B, C, E leżą na okręgu w w tej właśnie kolejności. Okrąg w' przechodzący przez punkt C przecina odcinki BC i EC odpowiednio w punktach X i Y. Punkty Y, X, C oraz F leżą w tej właśnie kolejności na okręgu w'. Wiedząc, że miara kąta XFY wynosi 40 stopni, oblicz miarę kąta BAE.
Rozwiązanie
W jaki sposób możemy obliczyć miarę kąta BAE? Pierwszym pomysłem mogłoby być wyznaczenie najpierw miar pozostałych kątów czworokąta ABCE. Ale wygląda na to, że nie mamy szans poznać miar kątów ABC i AEC... Jeśli jednak skorzystamy z warunku (1) dla czworokąta ABCE, okazuje się, że kątami ABC i AEC możemy się w ogóle nie przejmować. W czworokącie ABCE miary naprzeciwległych kątów sumują się do 180 stopni, więc żeby wyznaczyć miarę kąta BAE, wystarczy odjąć miarę kąta BCE od 180 stopni.
A skąd weźmiemy miarę kąta BCE? Do tego przyda się okrąg w'. Zauważmy, że szukany kąt BCE to ten sam kąt, co XCY. Kąt XCY oraz XFY są wpisane w okrąg w' i oparte na tym samym łuku, więc mają tę samą miarę - 40 stopni (można też powiedzieć, że używamy warunku (2) dla czworokąta XCFY, wpisanego w okrąg w'). Teraz możemy wykonać ostatnie obliczenie: miara kąta BCE wynosi 40 stopni, więc miara kąta BAE jest równa 180 - 40 = 140 stopni.
Dużo ciekawsze niż obliczenia miar kątów przy użyciu warunków (1) i (2) są zadania, w których trzeba wykazać, że na pewnym czworokącie można opisać okrąg. Poniżej znajdują się dwa ładne i ciekawe przykłady - pierwszy pokazuje przy okazji, jak wykorzystać fakt, że
kąty wpisane w okrąg w oparte na łukach równej długości mają równe miary.
Przykład 2 (Zadanie 6)
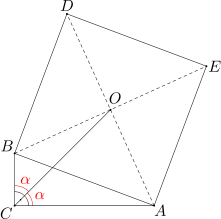
Dany jest trójkąt prostokątny ABC o kącie prostym przy wierzchołku C. Na boku AB tego trójkąta zbudowano po jego zewnętrznej stronie kwadrat ABDE o środku O. Wykaż, że kąty ACO i BCO mają równe miary.
Rozwiązanie
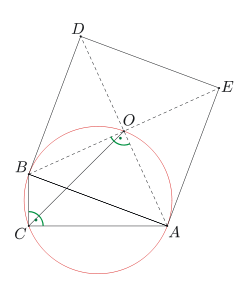
Wygląda na to, że trudno byłoby bezpośrednio obliczyć miary kątów ACO i BCO, żeby wykazać, że są równe. Wobec tego lepszą drogą jest powiązanie ich jakoś ze sobą na rysunku, żeby otrzymać jakiś związek pomiędzy ich miarami. Gdyby na przykład były to kąty wpisane w pewien okrąg, to być może udałoby się coś takiego osiągnąć. Czy istnieje taki okrąg? Musiałby on zawierać punkty A, B, C i O, czyli byłby to okrąg opisany na czworokącie ACBO. Chcemy więc udowodnić, że na czworokącie ACBO można opisać okrąg.
Ponieważ oba warunki równoważne tej własności mówią coś o miarach kątów, pomyślmy, co wiadomo o kątach czworokąta ACBO. Wprost z danych zadania wynika, że kąt ACB jest prosty. Wobec tego, żeby spełnić warunek (1), wystarczy udowodnić, że kąt BOA także jest prosty - wtedy oczywiście miary kątów ACB i BOA sumują się do 180 stopni. Ale miara kąta BOA jest równa 90 stopni - punkt O to punkt przecięcia przekątnych kwadratu, a odcinki AO i BO to połowy przekątnych, więc przecinają się pod kątem prostym, a ponadto są równe.
Czworokąt ACBO jest więc wpisany w okrąg, a kąty ACO i BCO są kątami wpisanymi w ten okrąg, opartymi na łukach AO i BO odpowiednio. Gdyby były oparte na tym samym łuku, to rozwiązanie byłoby zakończone - niestety nie jest tak dobrze, ale niewiele brakuje. Zauważyliśmy już, że odcinki AO i BO są równe - wobec tego odpowiadające im łuki, na których oparte są kąty ACO i BCO, mają równą długość. A kąty oparte na łukach równej długości mają tę samą miarę. (Dlaczego? Jeśli zostawimy w miejscu jeden łuk i oparty na nim kąt wpisany, a obrócimy resztę okręgu wokół jego środka, wraz z drugim kątem wpisanym, tak żeby drugi łuk pokrył się z pierwszym, to na rysunku zobaczymy dwa kąty wpisane oparte na tym samym łuku :-) Obrócenie kąta oczywiście nie zmieni jego miary.)
Kolejny przykład pokazuje, jak można próbować udowodnić, że istnieje okrąg opisany na danym pięciokącie. Ponieważ to zadanie ma rozwiązanie bardzo ładne i dające dużo satysfakcji, polecamy próby samodzielnego rozwiązania, przy ewentualnej pomocy wskazówek.
Przykład 3 (Zadanie 5)
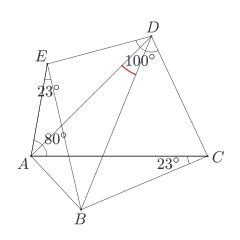
Dany jest pięciokąt wypukły ABCDE. Miary kątów ACB i AEB wynoszą po 23 stopnie. Miara kąta CAE równa się 80 stopni, a miara kąta CDE wynosi 100 stopni. Oblicz miarę kąta ADB.
Rozwiązanie
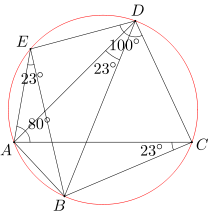
Popatrzmy na czworokąt ACDE: miara kąta CAE wynosi 80 stopni, a miara kąta CDE to 100 stopni - w sumie 180 stopni. Ten czworokąt spełnia warunek (1), więc jest wpisany w okrąg. Z interesującego nas kąta ten okrąg zawiera na pewno punkty A i D - a co z punktem B?
Przyjrzyjmy się teraz czworokątowi ABCE: miary kątów BCA i BEA wynoszą po 23 stopnie. Ponieważ ta para kątów jest taka, jakiej wymaga warunek (2), to korzystamy z tego warunku - czworokąt ABCE jest wpisany w okrąg. Ten okrąg z kolei zawiera z pewnością punkty A i B, ale nie wiemy, co z punktem D. A chcielibyśmy znaleźć okrąg, który zawiera punkty A, B i D.
A może dwa okręgi, które znaleźliśmy, są tak naprawdę jednym okręgiem?
Tak! Zauważmy, że okrąg opisany na czworokącie ACDE jest okręgiem opisanym na trójkącie ACE. Tak samo, okrąg opisany na czworokącie ABCE jest w szczególności opisany na trójkącie ACE. Ale istnieje dokładnie jeden okrąg opisany na danym trójkącie. Wobec tego te dwa okręgi to jeden okrąg, opisany na pięciokącie ABCDE!
Teraz wystarczy tylko zauważyć, że kąt ADB jest kątem wpisanym w okrąg opisany na danym pięciokącie. jest oparty na łuku AB - tym samym, na którym są oparte kąty AEB i ACB. Wobec tego jego miara jest równa 23 stopnie.
Wysokości trójkąta mają tę własność, że wraz z dodaniem ich do rysunku pojawia się kilka czworokątów, na których można opisać okręgi. Co za tym idzie, jest dużo możliwości porównywania i obliczania miar różnych kątów. Wobec tego jest to dobry temat do wielu zadań, a żeby się do niego przyzwyczaić i zapoznać z podstawami, zobaczmy przykład, który powinien pomóc w znalezieniu podejścia do pozostałych zadań, w których pojawiają się wysokości trójkąta.
Przykład 4 (Zadanie 12)
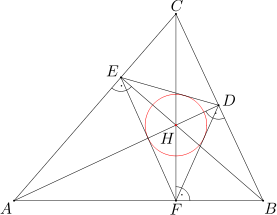
Dany jest trójkąt ostrokątny ABC. Wysokości AD, BE, CF tego trójkąta przecinają się w punkcie H. Wykaż, że punkt H jest środkiem okręgu wpisanego w trójkąt DEF.
Rozwiązanie
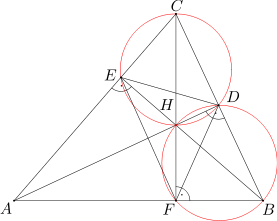
Środek okręgu wpisanego w trójkąt DEF znajduje się w punkcie przecięcia jego dwusiecznych. Wobec tego chcielibyśmy udowodnić, że odcinek DH dzieli kąt EDF na pół, odcinek EH dzieli kąt FED na pół, a odcinek FH dzieli kąt DFE na pół. Ponieważ dowody wszystkich trzech stwierdzeń przebiegają prawie tak samo, wykażemy tylko pierwsze, pozostawiając dwa dalsze do samodzielnego przećwiczenia. Udowodnimy więc, że kąty EDH i FDH są równe, czyli są połowami kąta EDF.
Zaczniemy od przedstawienia ogólnego faktu, który warto zapamiętać, bo przyda się pewnie w większości zadań z tego działu, które wymagają narysowania wysokości trójkąta: na każdym z czworokątów AEHF, BDHF i CEHD można opisać okrąg. Dowód jest bardzo łatwy: odcinek EH jest prostopadły do AE, bo jest zawarty w wysokości opuszczonej na bok AC, tak samo odcinki HF i AF są prostopadłe - wobec tego kąty AEH i AFH sumują się do 180 stopni i z warunku (1) na czworokącie AEHF można opisać okrąg. Dla pozostałych dwóch czworokątów argument jest identyczny.
Wracamy do równości miar kątów EDH i FDH. Wykorzystamy dwa ze znalezionych przed chwilą okręgów opisanych. Po pierwsze, ponieważ na czworokącie CEHD możemy opisać okrąg, to z warunku (2) miary kątów EDH i ECH są równe. Po drugie, ponieważ na czworokącie BDHF możemy opisać okrąg, to z warunku (2) miary kątów FDH i FBH są równe. Wobec tego wystarczy, że wykażemy, że kąty ECH i FBH mają taką samą miarę.
W tym celu przyjrzyjmy się trójkątom ACF i ABE: mają one wspólny kąt BAC, ponadto każdy z nich ma kąt prosty (AFC i AEB), a trzeci kąt to odpowiednio ACF, czyli ECH, oraz ABE, czyli FBH. Stąd widać, że \(\angle ECH = 180^\circ - \angle BAC = \angle FBH\), co kończy dowód.
Na koniec przykład zadania, które przypomina dobrze znany, ale przydatny w zadaniach fakt: kąt wpisany oparty na średnicy ma miarę 90 stopni; i w drugą stronę: jeśli kąt wpisany ma miarę 90 stopni, to jest oparty na średnicy. Ponieważ metody, które trzeba zastosować oprócz tego faktu zostały już dokładnie omówione, zostawiamy ciąg wskazówek do pomocy przy samodzielnym rozwiązaniu.
Przykład 5 (Zadanie 15)
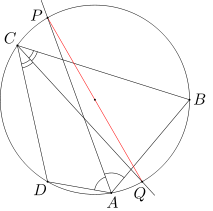
Czworokąt wypukły ABCD jest wpisany w okrąg w. Dwusieczna kąta BAD przecina okrąg w w punkcie P, a dwusieczna kąta BCD przecina okrąg w w punkcie Q. Udowodnij, że odcinek PQ jest średnicą okręgu w.
Rozwiązanie
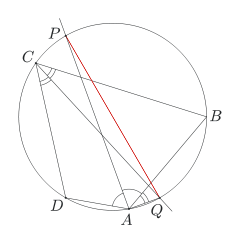
Spróbujmy wykazać, że kąt QAP jest prosty. Jego częścią jest kąt BAP - połowa kąta DAB. Wobec tego chcielibyśmy się dowiedzieć czegoś o pozostałej części, czyli o kącie QAB. (Oczywiście kąt QCP byłby równie dobry w rozwiązaniu, jak wybrany kąt QAP. A gdyby rysunek wyszedł inaczej i punkt A leżałby po drugiej stronie prostej PQ, to trzebaby podzielić kąt QAP na kąty QAD i DAP.)
Kąty QAB i QCB są wpisane w okrąg w, oparte na tym samym łuku. Wobec tego miara kąta QAB to połowa miary kąta BCD.
Podsumowując, miara kąta QAP to połowa sumy miar kątów DAB i BCD - ile to jest?
Wystarczy sobie przypomnieć, że czworokąt ABCD jest wpisany w okrąg. Z warunku (1) naprzeciwległe kąty DAB i BCD sumują się do 180 stopni. Stąd miara kąta QAP to połowa ze 180 stopni, czyli ten kąt jest prosty.
