Zaprezentowane rozwiązania są tylko przykładami prawidłowych rozwiązań - większość z zadań można bowiem rozwiązać na wiele sposobów. Zachęcamy Czytelników do podjęcia samodzielnej próby znalezienia własnych metod rozwiązania.
Zadanie 1
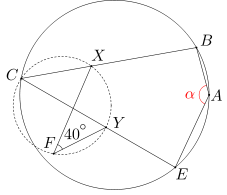
Punkty A, B, C, E leżą na okręgu w w tej właśnie kolejności. Okrąg w' przechodzący przez punkt C przecina odcinki BC i EC odpowiednio w punktach X i Y. Punkty Y, X, C oraz F leżą w tej właśnie kolejności na okręgu w'. Wiedząc, że miara kąta XFY wynosi 40 stopni, oblicz miarę kąta BAE.
Ponieważ czworokąt ABCE jest wpisany w okrąg, więc suma miar kątów BCE i BAE wynosi 180 stopni. Stąd miara kąta BAE równa się 180-40=140 stopni.
Zadanie 2
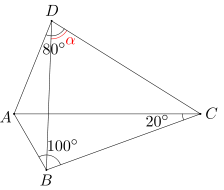
Dany jest czworokąt wypukły ABCD. Miary kątów ABC, BCA i ADC wynoszą odpowiednio 100, 20 i 80 stopni. Oblicz miarę kąta BDC.
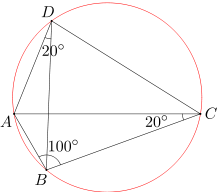
Ponieważ suma miar kątów ABC i CDA wynosi 180 stopni, więc na czworokącie ABCD można opisać okrąg. Stąd wynika, że miara kąta ADB jest równa mierze kąta ACB (są to kąty wpisane oparte na tym samym łuku). Wobec tego miara kąta ADB równa się 20 stopni. Ostatecznie więc miara kąta BDC wynosi 80-20=60 stopni.
Zadanie 3
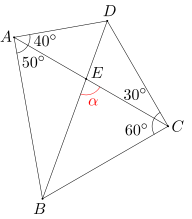
Dany jest czworokąt wypukły ABCD. Miary kątów BAC, CAD, ACB i ACD wynoszą odpowiednio 50, 40, 60, 30 stopni. Przekątne AC i BD przecinają się w punkcie E. Oblicz miarę kąta BEC.
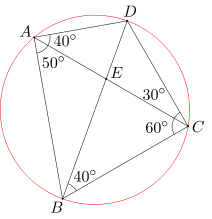
Ponieważ suma miar kątów BAD i BCD wynosi 180 stopni, więc na czworokącie ABCD można opisać okrąg. Stąd wynika, że miara kąta CBD jest równa mierze kąta CAD(są to kąty wpisane oparte na tym samym łuku). Wobec tego miara kąta CBD równa się 40 stopni. Ostatecznie więc miara kąta BEC wynosi 180-40-60=80 stopni.
Zadanie 4
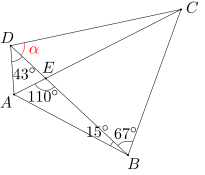
Dany jest czworokąt wypukły ABCD. Przekątne AC i BD przecinają się w punkcie E. Miary kątów ADB, DBC, AEB i ABD wynoszą odpowiednio 43, 67, 110, 15 stopni. Oblicz miarę kąta BDC.
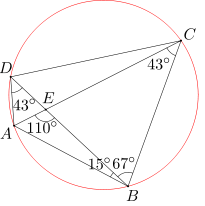
W trójkącie BEC miara kąta zewnętrznego przy wierzchołku E jest równa sumie miar kątów wewnętrznych przy wierzchołkach B i C. Wobec tego miara kąta ACB wynosi 110-67=43 stopni. Miary kątów ADB i ACB są więc równe, a więc na czworokącie ABCD można opisać okrąg. A zatem suma miar kątów ABC i CDA wynosi 180 stopni. Stąd wynika, że miara kąta BDC równa się 180-15-67-43=55 stopni.
Zadanie 5
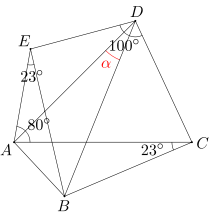
Dany jest pięciokąt wypukły ABCDE. Miary kątów ACB i AEB wynoszą po 23 stopnie. Miara kąta CAE równa się 80 stopni, a miara kąta CDE wynosi 100 stopni. Oblicz miarę kąta ADB.
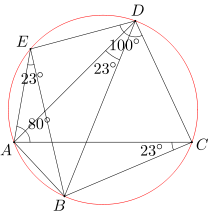
Ponieważ miary kątów ACB i AEB są równe, więc na czworokącie ABCE można opisać okrąg. Innymi słowy: okrąg opisany na trójkącie ACE przechodzi przez punkt B. Ponieważ suma miar kątów CAE i CDE wynosi 180 stopni, więc na czworokącie ACDE można opisać okrąg. Innymi słowy: okrąg opisany na trójkącie ACE przechodzi przez punkt D.
Wobec tego okrąg opisany na trójkącie ACE przechodzi przez punkt B i D, co oznacza, że na pięciokącie ABCDE można opisać okrąg. Wobec tego miara kąta ADB jest równa mierze kąta ACB (są to kąty wpisane oparte na tym samym łuku). Stąd ostatecznie miara kąta ADB wynosi 23 stopnie.
Zadanie 6
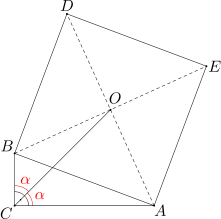
Dany jest trójkąt prostokątny ABC o kącie prostym przy wierzchołku C. Na boku AB tego trójkąta zbudowano po jego zewnętrznej stronie kwadrat ABDE o środku O. Wykaż, że kąty ACO i BCO mają równe miary.
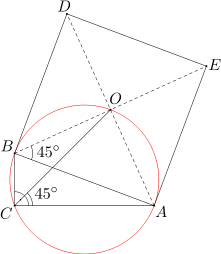
Ponieważ punkt O jest środkiem kwadratu ABDE, więc miara kąta AOB wynosi 90 stopni, a miara kąta ABO równa się 45 stopni. Wobec tego suma miar kątów ACB i AOB wynosi 180 stopni, a zatem na czworokącie ACBO można opisać okrąg. Stąd wynika, że kąt ACO ma tę samą miarę co kąt ABO (oba kąty są wpisane oparte na tym samym łuku). Zatem miara kąta ACO wynosi 45 stopni. Stąd wniosek, że miara kąta BCO równa się 90-45=45 stopni, co dowodzi, że oba kąty ACO i BCO są równe.
Zadanie 7
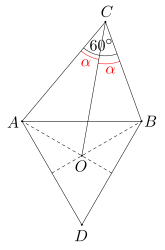
Dany jest trójkąt ABC, w którym miara kąta przy wierzchołku C wynosi 60 stopni. Na boku AB tego trójkąta zbudowano po jego zewnętrznej stronie trójkąt równoboczny ABD o środku O. Wykaż, że kąty ACO i BCO mają równe miary.
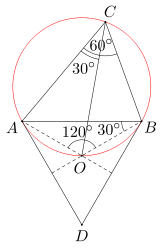
Ponieważ punkt O jest środkiem trójkąta równobocznego ABD, więc miara kąta AOB wynosi 120 stopni, a miara kąta ABO równa się 30 stopni. Wobec tego suma miar kątów ACB i AOB wynosi 180 stopni, a zatem na czworokącie ACBO można opisać okrąg. Stąd wynika, że miara kąta ACO jest równa mierze kąta ABO (oba kąty są wpisane oparte na tym samym łuku). Zatem miara kąta ACO wynosi 30 stopni. Stąd wniosek, że miara kąta BCO równa się 60-30=30 stopni, co dowodzi, że oba kąty ACO i BCO są równe.
Zadanie 8
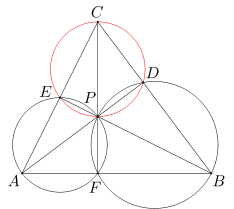
Punkt P leży wewnątrz trójkąta ABC. Proste AP, BP, CP przecinają odcinki BC, CA, AB odpowiednio w punktach D, E, F. Wykaż, że jeżeli na czworokątach AFPE i BDPF można opisać okręgi, to także na czworokącie CEPD można opisać okrąg.
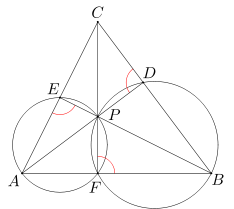
Ponieważ na czworokącie AFPE można opisać okrąg, więc kąt wewnętrzny przy wierzchołku E czworokąta APFE jest równy kątowi zewnętrznemu przy wierzchołku F tego czworokąta. Wynika stąd, że miara kąta AEP równa się mierze kąta BFP.
Analogicznie, ponieważ na czworokącie BDPF można opisać okrąg, więc kąt wewnętrzny przy wierzchołku F czworokąta BDPF jest równy kątowi zewnętrznemu przy wierzchołku D tego czworokąta. Wobec tego miara kąta BFP równa się mierze kąta CDP.
Z powyższych rozważań wynika więc, że kąt wewnętrzny przy wierzchołku D czworokąta CEPD jest równy kątowi zewnętrznemu przy wierzchołku E tego czworokąta. A zatem na czworokącie CEPD można opisać okrąg.
Zadanie 9
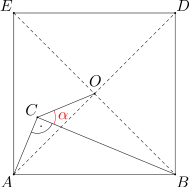
Dany jest trójkąt prostokątny ABC o kącie prostym przy wierzchołku C, w którym AC<BC. Na boku AB tego trójkąta zbudowano po jego wewnętrznej stronie kwadrat ABDE o środku O. Wyznacz miarę kąta BCO.
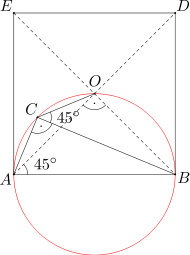
Ponieważ punkt O jest środkiem kwadratu, więc kąt AOB jest prosty, a miara kąta BAO wynosi 45 stopni. Ponieważ kąty ACB i AOB są równe, więc na czworokącie ABOC można opisać okrąg. Stąd wynika, że miara kąta BCO jest równa mierze kąta BAO, gdyż oba te kąty są wpisane oparte na tym samym łuku. Zatem miara kąta BCO równa się 45 stopni.
Zadanie 10
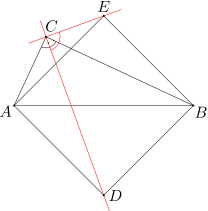
Dany jest trójkąt ABC, w którym kąt przy wierzchołku C jest prosty oraz AC<BC. Niech ADBE będzie kwadratem o przekątnej AB. Udowodnij, że proste CD i CE są prostopadłe.
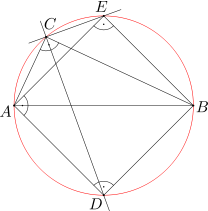
Ponieważ kąty ACB i AEB mają równe miary, więc na czworokącie ABEC można opisać okrąg - średnicą tego okręgu jest odcinek AB. Ten sam okrąg jest opisany na kwadracie ADBE. Wobec tego punkty A, D, B, E, C leżą na okręgu o średnicy AB.
Stąd wynika, że miara kąta DCE jest równa mierze kąta DAE (oba kąty są kątami wpisanymi opartymi na tym samym łuku), a ponieważ kąt DAE jest prosty, więc kąt DCE także jest prosty.
Zadanie 11
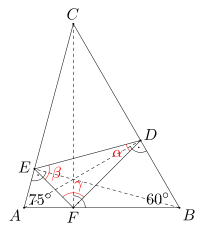
Miary kątów przy wierzchołkach A i B trójkąta ABC wynoszą odpowiednio 75 i 60 stopni. Odcinki AD, BE, CF są wysokościami trójkąta ABC. Wyznacz miary kątów trójkąta DEF.
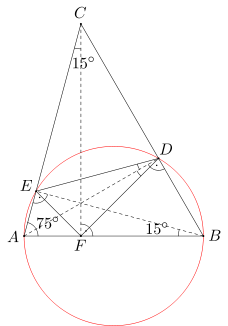
Ponieważ kąty ADB i AEB są równe, więc na czworokącie ABDE można opisać okrąg. Wobec tego miara kąta ADE jest równa mierze kąta ABE (oba kąty są wpisane oparte na tym samym łuku). Z kolei miara kąta ABE wynosi 90-75=15 stopni. A zatem miara kąta ADE równa się 15 stopni.
Analogicznie wyznaczamy miarę kąta ADF: Ponieważ kąty ADC i AFC są równe, więc na czworokącie AFDC można opisać okrąg. Wobec tego miara kąta ADF jest równa mierze kąta ACF (oba kąty są wpisane oparte na tym samym łuku). Z kolei miara kąta ACF wynosi 90-75=15 stopni. A zatem miara kąta ADF równa się 15 stopni.
Stąd wniosek, że miara kąta EDF równa się 15+15=30 stopni. Analogicznie obliczamy miarę kąta DEF. Wynosi ona 60 stopni. W rezultacie miara kąta DFE równa się 180-30-60=90 stopni.
Stąd ostatecznie miary kątów trójkąta DEF wynoszą 30, 60 i 90 stopni.
Zadanie 12
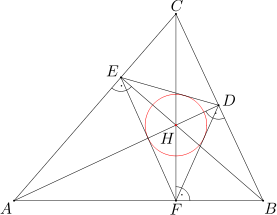
Dany jest trójkąt ostrokątny ABC. Wysokości AD, BE, CF tego trójkąta przecinają się w punkcie H. Wykaż, że punkt H jest środkiem okręgu wpisanego w trójkąt DEF.
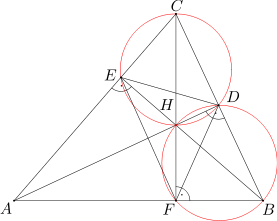
Zauważmy, że trójkąty ACF i ABE są prostokątne i mają wspólny kąt przy wierzchołku A. Zatem kąty ABH i ACH są równe.
Na czworokącie BDHF można opisać okrąg, ponieważ suma miar kątów HFB i HDB jest równa 180 stopni. Analogicznie, na czworokącie CEHD można opisać okrąg, ponieważ suma miar kątów CEH i CDH wynosi 180 stopni. Stąd dostajemy
\(\angle FDH=\angle ABH=\angle ACH=\angle EDH.\)
Z uzyskanej równości wynika, że punkt H leży na dwusiecznej kąta przy wierzchołku D trójkąta DEF.
Analogicznie dowodzimy, że punkt H leży na dwusiecznej kątów wewnętrznych pozostałych kątów trójkąta DEF. Wobec tego punkt H jest środkiem okręgu wpisanego w trójkąt DEF.
Zadanie 13
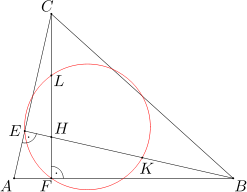
Dany jest trójkąt ostrokątny ABC. Wysokości BE i CF tego trójkąta przecinają się w punkcie H. Punkty K i L są odpowiednio środkami odcinków BH i CH. Wykaż, że punkty E, F, K, L leżą na jednym okręgu.

Ponieważ punkt K jest środkiem przeciwprostokątnej BH w trójkącie prostokątnym BFH, więc punkt K jest środkiem okręgu opisanego na trójkącie BFH. Kąt FKH jest kątem środkowym opartym na łuku HF, a kąt HBF jest kątem wpisanym opartym na łuku HF. Stąd wynika, że
\(\angle EKF=2\angle EBF.\)
Analogicznie dowodzimy, że
\(\angle ELF=2\angle ECF.\)
Ponadto
\(\angle EBF=90^\circ-\angle BAC=\angle ECF.\)
Łącząc powyższe równości stwierdzamy, że kąty EKF i ELF są równe. Wobec tego na czworokącie EFKL można opisać okrąg.
Zadanie 14
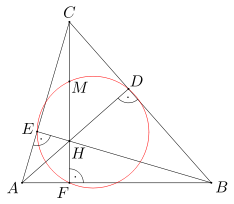
Dany jest trójkąt ostrokątny ABC. Wysokości AD, BE, CF tego trójkąta przecinają się w punkcie H. Punkt M jest środkiem odcinka CH. Wykaż, że punkty D, E, F, M leżą na jednym okręgu.
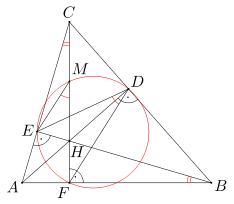
Ponieważ kąty HDC i HEC są proste, więc na czworokącie CEHD można opisać okrąg. Punkt M jest środkiem przeciwprostokątnej trójkąta CDH, a ponieważ okrąg opisany na czworokącie CEHD jest także okręgiem opisanym na trójkącie CEH, więc punkt M jest środkiem okręgu opisanego na czworokącie CEHD. Stąd uzyskujemy
\({1\over 2}\angle EMF=\angle ACF=90^\circ-\angle BAC=\angle ABE.\)
Ponadto, punkty A, B, D, E leżą na jednym okręgu, gdyż kąty ADB i AEB są równe. Stąd oraz z zadania 12 uzyskujemy
\(\angle ABE=\angle ADE={1\over 2}\angle EDF.\)
Porównując uzyskane równości wnioskujemy, że kąty EDF i EMF są równe. Stąd wynika, że punkty E, F, D, M leżą na jednym okręgu.
Zadanie 15
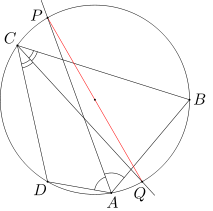
Czworokąt wypukły ABCD jest wpisany w okrąg w. Dwusieczna kąta BAD przecina okrąg w w punkcie P, a dwusieczna kąta BCD przecina okrąg w w punkcie Q. Udowodnij, że odcinek PQ jest średnicą okręgu w.
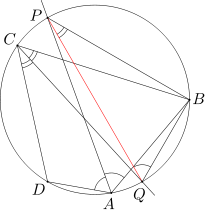
Kąty QCB i QPB są kątami wpisanymi opartymi na tym samym łuku, a więc są równe. Analogicznie, kąty PAB i PQB są równe. Wobec tego uzyskujemy
\(\angle QPB+\angle PQB=\angle QCB+\angle PAB= {1\over 2}\angle BCD+{1\over 2}\angle BAD={1\over2}\cdot 180^\circ= 90^\circ.\)
Stąd wynika, że miara kąta PBQ równa się 180-90=90 stopni. A zatem odcinek PQ jest średnicą okręgu w.
Zadanie 16
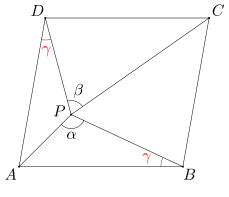
Punkt P leży wewnątrz równoległoboku ABCD, przy czym suma kątów APB i CPD wynosi 180 stopni. Wykaż, że kąty ABP i ADP są równe.
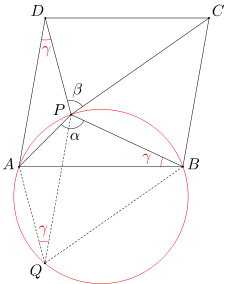
Niech Q będzie takim punktem, że czworokąt ADPQ jest równoległobokiem. Wówczas odcinki AD i PQ są równe i równoległe. Ponieważ czworokąt ABCD jest równoległobokiem, więc odcinki AD i BC są równe i równoległe. Wynika stąd, że odcinki BC i PQ są równe i równoległe, a zatem czworokąt BCPQ jest równoległobokiem.
Wobec tego AB=CD, AQ=DP oraz BQ=CP, co oznacza, że trójkąty ABQ i CDP są przystające. Stąd wniosek, że miara kąta CPD równa się mierze kąta BQA. A zatem suma miar kątów BQA i APB wynosi 180 stopni, co oznacza, że na czworokącie AQBP można opisać okrąg. Stąd uzyskujemy
\(\angle ABP=\angle AQP=\angle ADP,\)
co należało udowodnić.
