Skip to Content

Czworokąty wpisane w okrąg

strict warning: Only variables should be passed by reference in /var/www/uczesie/modules/book/book.module on line 560.
śr., 09/15/2010 - 10:15 — ciebie

O ile na każdym trójkącie da się opisać okrąg (tzn. dla każdego trójkąta istnieje okrąg - i to dokładnie jeden - który przechodzi przez wszystkie jego wierzchołki), o tyle istnieją czworokąty, na których okręgu opisać się nie da. Przykładem takiego czworokąta jest romb, który nie jest kwadratem. Charakteryzację takich czworokątów, na których da się opisać okrąg opisują następujące dwa twierdzenia.

Twierdzenie 1:

Dany jest czworokąt wypukły ABCD. Wówczas jeśli na czworokącie ABCD można opisać okrąg, to suma miar kątów DAB i BCD wynosi 180 stopni. Również odwrotnie: jeśli w czworokącie wypukłym ABCD suma miar kątów DAB i BCD wynosi 180 stopni, to na tym czworokącie da się opisać okrąg.


Dlaczego tak jest?
Żeby zrozumieć, skąd się bierze ta zasada, zobaczmy dowód pierwszej połowy twierdzenia. Przez O oznaczmy środek okręgu opisanego na czworokącie ABCD. Kąt DOB to kąt środkowy oparty na tym samym łuku, co kąt wpisany DAB, więc ma dwukrotnie większą miarę. Tak samo, kąt BOD to kąt środkowy oparty na tym samym łuku, co kąt wpisany BCD. Kąty DOB i BOD sumują się do kąta pełnego, więc mairy kątów DAB i BCD sumują się do 360:2 = 180 stopni. Dowód w drugą stronę wymaga trochę bardziej zaawansowanych narzędzi, ale ten argument daje dobrą intuicję odnośnie tego twierdzenia.

Czasami warunek suma miar kątów DAB i BCD w czworokącie ABCD wynosi 180 stopni wygodnie jest wysłowić w następujący sposób: kąt wewnętrzny przy wierzchołku A czworokąta ABCD jest równy kątowi zewnętrznemu przy wierzchołku C tego czworokąta.

Twierdzenie 2:

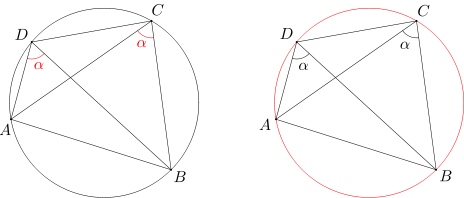
Dany jest czworokąt wypukły ABCD. Wówczas jeśli na czworokącie ABCD można opisać okrąg, to miary kątów ACB i ADB są równe. Również odwrotnie: jeśli w czworokącie wypukłym ABCD miary kątów ACB i ADB są równe, to na tym czworokącie da się opisać okrąg.


Dlaczego tak jest?
Znowu, łatwo pokazać argument dla pierwszej połowy twierdzenia. Opiszmy okrąg na czworokącie ABCD. Wystarczy zauważyć, że kąty ACB i ADB to kąty wpisane oparte na tym samym łuku, więc mają tę samą miarę. Dowód drugiej połowy jest trudniejszy, więc poprzestaniemy na intuicji z dowodu pierwszej połowy.



Theme by Dr. Radut.