Dobre przećwiczenie zadań o kątach w okręgu jest konieczne, żeby praca nad następnymi tematami: prostymi stycznymi do okręgów, okręgami stycznymi i czworokątami wpisanymi w okrąg, przebiegała szybko i sprawnie. Jeśli uda się opanować podstawowe metody związane z kątami wpisanymi opartymi na tym samym łuku i z zależnością pomiędzy kątami środkowymi i wpisanymi tak, żeby wykonywać je prawie mechanicznie, bez wracania do treści twierdzeń, to będzie dużo łatwiej zrozumieć rozwiązania zadań dotyczących dalszych zagadnień. Wobec tego pokażemy w kolejnych przykładach, jak używać twierdzeń z tego rozdziału i w jakich sytuacjach mogą one być potrzebne. Znajdują się tu przykłady zarówno bardzo łatwe, żeby przybliżyć temat tym, którzy widzą go po raz pierwszy, jak i trudniejsze zadania, z rozwiązaniami przedstawionymi w formie ciągów kolejnych spostrzeżeń - można ich użyć do sprawdzenia swoich umiejętności, rozwiązując samodzielnie, traktując ewentualnie kolejne kroki rozwiązania jako wskazówki.
Zaczniemy od faktu, który trzeba nie tylko zapamiętać, ale też umieć zastosować nawet w środku nocy: trójkąt, którego dwa wierzchołki leżą na pewnym okręgu, a trzeci jest środkiem tego okręgu, jest równoramienny. Dlaczego? Po prostu dwa jego boki, prowadzące od środka okręgów do punktów na jego brzegu, są promieniami, więc są równe.
Przykład 1 (Zadanie 2)
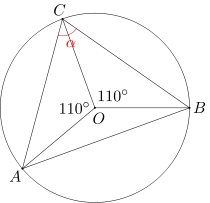
Punkt O jest środkiem okręgu opisanego na trójkącie ABC. Miary kątów AOC i BOC wynoszą po 110 stopni. Wyznacz miarę kąta ACB.
Rozwiązanie
Zauważmy najpierw, że kąt ACB jest sumą kątów ACO i OCB, które będziemy mogli łatwo wyznaczyć.
Z podanego powyżej faktu wynika, że trójkąt AOC jest równoramienny (OA = OC). Wobec tego miary kątów OAC i OCA są równe (180-110)/2 = 70/2 = 35 stopni. Tak samo trójkąt BOC jest równoramienny i miary kątów OBC oraz OCB wynoszą 35 stopni.
Wobec tego miara kąta ACB, równa sumie miar kątów ACO i OCB, wynosi 35 + 35 = 70 stopni.
Uwaga: to i następne zadanie można równie krótko rozwiązać, korzystając z relacji pomiędzy miarami kąta środkowego i wpisanego - zobacz rozwiązanie na stronie z zadaniami.)
Kolejne, trochę trudniejsze zadanie, dobrze potraktować jako okazję do próby samodzielnego rozwiązania z ewentualną pomocą wskazówek.
Przykład 2 (Zadanie 4)
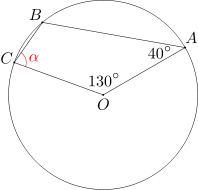
Dany jest czworokąt wypukły ABCO, w którym kąt AOC ma miarę 130 stopni, a kąt OAB ma miarę 40 stopni. Okrąg o środku O przechodzący przez punkt A przechodzi także przez punkty B i C. Wyznacz miarę kąta BCO.
Rozwiązanie
Dorysujmy promień OB - teraz mamy na rysunku trójkąt równoramienny OBC, zawierający szukany kąt. Ale poza tym o tym trójkącie wiemy zbyt niewiele, żeby coś policzyć. Ale mamy też trójkąt, o którym wiemy więcej...
Po dorysowaniu promienia OB powstał również trójkąt ABO, w którym kąt OAB ma miarę 40 stopni. Ponieważ ten trójkąt jest równoramienny (OA = OB), to miara kąta ABO także jest równa 40 stopni. Wobec tego miara kąta AOB to 180-40-40 = 100 stopni. Jakie informacje możemy stąd otrzymać na temat trójkąta OBC?
Ponieważ kąt AOC o mierze 130 stopni jest sumą kąta AOB o mierze 100 stopni i kąta BOC, to miara kąta BOC jest równa 130-100 = 30 stopni. Wiemy, że miary kątów OBC i BCO są równe, więc \(\angle OBC + \angle OCB + 30^\circ = 180^\circ\), a stąd \(2\cdot \angle BCO = 150^\circ\) i ostatecznie \(\angle BCO = 75^\circ\).
Po zapoznaniu się z najbardziej podstawowym faktem z tego rozdziału przejdźmy do równie ważnych - kątów środkowych i wpisanych oraz zależności między nimi. Mamy do zapamiętania dwa podstawowe narzędzia:
(1) kąt środkowy oparty na pewnym łuku ma dwa razy większą miarę, niż kąt wpisany oparty na tym samym łuku, (Twierdzenie 1)
(2) dwa kąty wpisane oparte na tym samym łuku mają tę samą miarę. (Twierdzenie 3)
Czasami przydaje się jeszcze trochę mocniejsza wersja drugiego narzędzia:
(2') dwa kąty wpisane oparte na łukach o tej samej długości mają tę samą miarę. (Twierdzenie 3)
Żeby te własności lepiej zapamiętać, przejdźmy do ćwiczeń. Przykłady 3 i 4 dotyczą kątów środkowych i wpisanych, przykład 5 korzysta z własności kątów wpisanych opartych na tym samym łuku, natomiast przykład 6 to ćwiczenie na koniec tego tematu.
Przykład 3 (Zadanie 7)
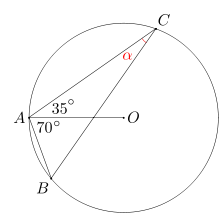
Trójkąt ABC, w którym miara kąta przy wierzchołku A wynosi 105 stopni, jest wpisany w okrąg o środku O. Miara kata CAO równa się 35 stopni. Wyznacz miarę kąta ACB.
Rozwiązanie
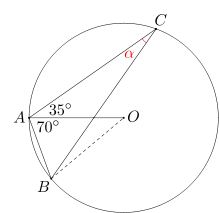
W jaki sposób powiązać kąt ACB z innymi kątami na rysunku, żeby dowiedzieć się czegoś o jego mierze? Zauważmy, że na rysunku mamy też kąt środkowy oparty na tym samym łuku - kąt AOB. Wobec tego miara kąta ACB jest połową miary kąta AOB. Czy umiemy wyznaczyć miarę kąta AOB?
Kąt BAC o mierze 105 stopni jest sumą kata CAO o mierze 35 stopni i kąta OAB. Wobec tego miara kąta OAB jest równa 105 - 35 = 70 stopni. Teraz przyda się poprzednio omawiane zagadnienie: trójkąt OAB jest równoramienny, więc miara kąta ABO jest równa mierze kąta OAB. Stąd miara kąta AOB jest równa 180 - 70 - 70 = 40 stopni. Wobec tego miara kąta ACB to 40:2 = 20 stopni.
Przykład 4 (Zadanie 13)
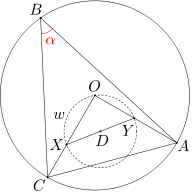
Punkt O jest środkiem okręgu opisanego na trójkącie ostrokątnym ABC. Punkty X, Y leżą na odpowiednio na odcinkach OC i OA. Punkt D jest środkiem odcinka XY. Środek okręgu opisanego na trójkącie OXY pokrywa się z punktem D. Wyznacz miarę kąta ABC.
Rozwiązanie
Pomyślmy, co możemy wnioskować z dość niezrozumiałej na pierwszy rzut oka informacji, że środek okręgu opisanego na trójkącie OXY leży w środku jednego z jego boków. Twierdzenie 2, które omówimy dokładniej jeszcze dalej, pomoże nam to zinterpretować. Ponieważ XY jest średnicą okręgu opisanego na trójkącie OXY, z tego twierdzenia wynika, że kąt YOX jest prosty.
Dalej już będzie łatwo. Oznaczmy przez w okrąg opisany na trójkącie ABC. Ponieważ kąt YOX jest tym samym, co kąt AOC, to wiemy, że kąt środkowy w okręgu w oparty na łuku CA ma miarę 90 stopni. A szukany kąt ABC jest wpisany (w okręgu w) oparty na tym samym łuku, co kąt AOC, to ma miarę o połowę mniejszą, czyli 45 stopni.
Przykład 5 (Zadanie 20)
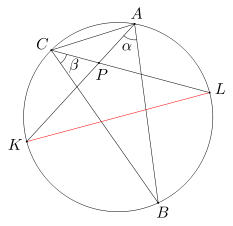
Punkt P leży wewnątrz trójkąta ABC, przy czym suma miar kątów PAB i PCB wynosi 90 stopni. Niech w będzie okręgiem opisanym na trójkącie ABC. Prosta AP przecina okrąg w w punkcie K, a prosta CP przecina okrąg w w punkcie L. Wykaż, że odcinek KL jest średnicą okręgu w.
Rozwiązanie
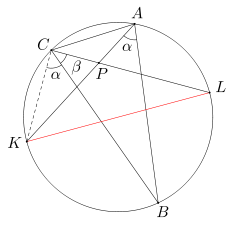
Żeby wykazać, że prosta KL jest średnicą okręgu, odwołamy się do Twierdzenia 2 (które jest dokładniej omówione dalej): wystarczy, że udowodnimy, że kąt wpisany oparty na łuku KL ma miarę 90 stopni.
Zastanówmy się, który kąt wpisany oparty na łuku KL wybrać do dowodu. Najlepiej taki, o którym już coś wiemy. Na przykład kąt KCL jest sumą kątów KCB i LCB. Kąt LCB jest tym samym, co kąt PCB, o którym mówią coś warunki zadania. Spróbujmy więc dowiedzieć się czegoś o drugiej części kąta KCL, czyli kącie KCB.
Możemy na przykład poszukać jakiegoś kąta wpisanego opartego na tym samym łuku, co kąt KCB. Na rysunku mamy na przykład kąt KAB, który spełnia ten warunek. Czy coś o nim wiemy? Jest to ten sam kąt, co wymieniony w treści zadania kąt PAB. Czyli kąt KCB ma tę samą miarę, co kąt PAB.
Wróćmy do kąta KCL - jest on sumą dwóch części, których miary są równe miarom kątów PCB i PAB. Ale z treści zadania wiemy, że miary tych kątów sumują się do 90 stopni. Wobec tego kąt KCL jest prosty, a stąd na mocy Twierdzenia 2 cięciwa KL jest średnicą danego okręgu.
Na koniec przykład z serią wskazówek, do samodzielnego przećwiczenia.
Przykład 6 (Zadanie 24)
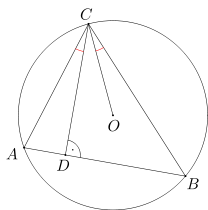
Punkt O jest środkiem okręgu opisanego na trójkącie ostrokątnym ABC. Punkt D jest rzutem prostokątnym punktu C na bok AB. Wykaż, że kąty ACD i BCO są równe.
Rozwiązanie
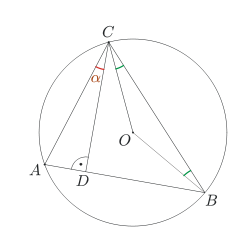
Popatrzmy na trójkąt ACD. Kąt ADC jest prosty, ponieważ punkt D został skonstruowany tak, że odcinek DC jest prostopadły do boku AB. Miarę kąta CAD możemy wobec tego zapisać jako \(180^\circ - 90^\circ - \alpha = 90^\circ - \alpha\). Jakie kąty teraz możemy opisać dokładniej?
Teraz użyjemy wiedzy o kątach środkowych i wpisanych: kąt COB jest środkowy, oparty na tym samym łuku, co kąt wpisany CAB. Wobec tego ma miarę dwukrotnie większą, czyli \(180^\circ - 2\alpha\). Czy już umiemy coś powiedzieć o mierze kąta BCO?
Ponieważ trójkąt OBC jest równoramienny (OB = OC - promienie okręgu), to miary kątów CBO i BCO są równe i wynoszą \((180^\circ - (180^\circ - 2\alpha))/2 = \alpha\), co należało udowodnić.
Poniższy przykład pokazuje ciekawe zastosowanie takiej własności: kąt wpisany oparty o średnicy ma miarę 90 stopni; i w drugą stronę: jeśli kąt wpisany oparty na łuku AB jest prosty, to cięciwa AB jest średnicą okręgu. (Twierdzenie 2)
Czy umiesz wyjaśnić, jak to wynika z własności (1)?
Używaliśmy jej we wcześniejszych przykładach, ale teraz omówimy dokładnie zastosowanie w trudniejszym i ciekawszym przypadku.
Przykład 7 (Zadanie 27)
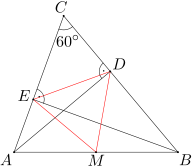
Dany jest trójkąt ostrokątny ABC, w którym miara kąta ACB wynosi 60 stopni. Punkty D i E są spodkami wysokości tego trójkąta poprowadzonymi odpowiednio z wierzchołków A i B. Punkt M jest środkiem boku AB. Udowodnij, że trójkąt DEM jest równoboczny.
Rozwiązanie
Przede wszystkim zauważmy, że punkty D i E są zdefiniowane tak, że ma rysunku pojawiają się dwa kąty proste: ADB i AEB. Co można z nimi zrobić? Chętnie zobaczylibyśmy na rysunku jakiś okrąg, żeby zastosować podane powyżej własności kątów - dowód, że pewien trójkąt jest równoboczny, można przeprowadzić, obliczając, że wszystkie jego kąty mają po 60 stopni. Poza tym powiedzieliśmy już, że przyda się tu własność (3). Spróbujmy więc opisać okrąg na trójkącie ABD - jeden z kątów prostych, ADB, jest kątem wpisanym w ten okrąg i może uda się coś z tego wywnioskować.
Istotnie, własność (3) mówi, że kąt ADB, jako wpisany kąt prosty, musi być oparty na średnicy okręgu. Czyli odcinek AB jest średnicą tego okręgu, a środek tego odcinka - punkt M - jest również środkiem okręgu! Zauważmy, że gdybyśmy wzięli trójkąt ABC zamiast ADB i opisali na nim okrąg, to doszlibyśmy do wniosku, że z tych samych powodów odcinek AB jest jego średnicą, a punkt M jego środkiem. Wobec tego okręgi opisane na trójkątach ABC i ABD są tym samym okręgiem (o środku M i promieniu MA)!
Teraz możemy przyjrzeć się kątom w tym okręgu. Na przykład kąt EMD, jeden z kątów trójkąta DEM, jest kątem środkowym w tym okręgu. Jak możemy znaleźć jego miarę? Możemy na przykład zauważyć, że kąt wpisany EAD jest oparty na tym samym łuku, a jego miarę łatwo wyznaczyć, patrząc na kąty trójkąta ACD. W tym trójkącie oprócz kąta EAD mamy kąt prosty ADC i kąt ACD o mierze 60 stopni. Wobec tego kąt CAD, czyli EAD, ma miarę 30 stopni, a EMD - dwukrotnie większą, czyli 60 stopni, jak powinno być w trójkącie równobocznym.
Okazuje się, że to już właściwie koniec rozwiązania. Trójkąt DEM jest przecież równoramienny - odcinki MD i ME są promieniami okręgu. Wobec tego miary kątów MDE i MED są równe i wynoszą (180 - 60):2 = 60 stopni, więc trójkąt DEM faktycznie jest równoboczny.
Uwaga: w rozwiązaniu tego zadania udowodniliśmy ważną własność, która przyda się kilkakrotnie podczas pracy nad pozostałymi problemami:
środkiem okręgu opisanego na trójkącie prostokątnym jest środek przeciwprostokątnej tego trójkąta.
Czasami w zadaniach pojawiają się informacje w rodzaju "długość łuku AB jest 1/6 długości całego okręgu" albo "dany okrąg ma długość 1, a łuk XY ma długość 1/18" - ogólnie, dowiadujemy się, jaki jest stosunek długości łuku pewnego okręgu do długości całego okręgu. Warto wiedzieć, co z taką informacją zrobić - na przykład, jak przetłumaczyć ją na język kątów w okręgu, którymi się tu zajmujemy. Najlepiej zapamiętać, że kąt środkowy jest takim ułamkiem kąta pełnego, jakim ułamkiem długości okręgu jest długość łuku, na którym jest oparty. W opisanych sytuacjach dowiedzielibyśmy się, że kąt środkowy oparty na łuku AB ma miarę 360:6 = 60 stopni (a kąt wpisany oparty na tym łuku - 30 stopni), natomiast kąt środkowy oparty na łuku XY ma miarę 360:18 = 20 stopni (a kąt wpisany oparty na tym łuku - 10 stopni). Zobaczmy, jak zastosować tę regułę w zadaniach - jedno rozwiązanie opisujemy dokładnie, drugie, trochę trudniejsze, podajemy w postaci serii wskazówek, więc dobrze je potraktować jako ćwiczenie.
Przykład 8 (Zadanie 16)
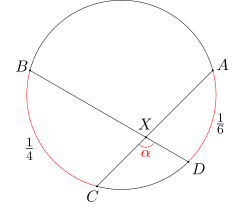
Punkty A, B, C, D leżą w tej właśnie kolejności na jednym okręgu w. Długość łuku BC stanowi 1/4 długości okręgu w. Długość łuku DA stanowi 1/6 długości okręgu w. Cięciwy AC i BD przecinają się w punkcie X. Wyznacz miarę kąta CXD.
Rozwiązanie
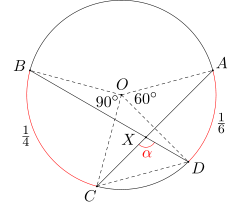
Zgodnie z powyższą regułą zinterpretujmy na początek informacje o długościach łuków. Dowiadujemy się z nich, że kąt środkowy oparty na łuku BC ma miarę 360:4 = 90 stopni, a kąt wpisany oparty na łuku BC ma miarę 90:2 = 45 stopni. Natomiast kąt środkowy oparty na łuku DA ma miarę 360:6 = 60 stopni, a kąt wpisany oparty na łuku DA ma miarę 60:2 = 30 stopni.
Żeby to jakoś wykorzystać, poszukajmy na rysunku kątów środkowych i wpisanych opartych na tych łukach. Z drugiej strony, zastanówmy się, jak powiedzieć coś o mierze kąta CXD. Bezpośrednio może być trudno czegoś się o nim dowiedzieć, bo punkt X ani nie leży na okręgu, ani nie jest jego środkiem. Ale może uda się coś wywnioskować na przykład z miar kątów w trójkącie CXD?
W tym miejscu oba podejścia powinny skleić się w jedno rozwiązanie. Umiemy wyznaczyć miary pozostałych kątów w trójkącie CXD: kątów XCD i XDC. Te kąty to kąty wpisane oparte odpowiednio na łukach DA i BC. Żeby to zauważyć, wystarczy przedłużyć ramię CX aż do punktu A, a ramię DX aż do punktu B. Wobec tego mamy równanie
\(\angle CXD = 180^\circ - \angle XCD - \angle XDC\),
i po podstawieniu obliczonych wcześniej wartości \(\angle CXD = 180^\circ - 30^\circ - 45^\circ = 105^\circ\).
Przykład 9 (Zadanie 17)
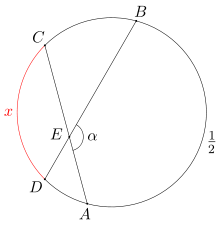
Punkty A, B, C, D leżą w tej właśnie kolejności na okręgu o długości 1. Długość łuku AB wynosi 1/2. Cięciwy AC i BD przecinają się w punkcie E, przy czym miara kąta AEB równa się α. Oblicz długość łuku CD.
Rozwiązanie
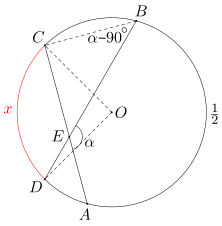
Pomyślmy teraz nad metodą dojścia do rozwiązania. W jaki sposób wyznaczyć długość pewnego łuku? Jakie wielkości w tym pomogą?
Łuk AB jest połową okręgu - to oznacza, że kąt środkowy oparty na tym łuku ma miarę 360:2 = 180 stopni. Czyli odcinek AB jest średnicą danego okręgu.
Pomyślmy teraz nad metodą dojścia do rozwiązania. W jaki sposób wyznaczyć długość pewnego łuku? Jakie wielkości w tym pomogą?
Zastosujemy naszą regułę odwrotnie niż zwykle: jeśli obliczymy miarę kąta środkowego opartego na łuku CD, a potem powiemy, jakim jest ułamkiem kąta pełnego, to będziemy wiedzieli, jakim ułamkiem długości całego okręgu jest łuk CD. Ponieważ znamy długość okręgu, to będziemy umieli wyznaczyć też długość tego łuku.
Być może nie umiemy od razu wyznaczyć miary kąta środkowego opartego na łuku CD - spróbujmy najpierw wyznaczyć miarę kąta wpisanego opartego na tym łuku. W tym celu popatrzmy na przykład na trójkąt ADE (BCE byłby równie dobry).
W trójkącie ADE mamy kąt ADE, który jest prosty, ponieważ jest tym samym, co kąt ADB oparty na średnicy. Umiemy też wyznaczyć miarę kąta AED - wraz z kątem AEB o mierze α sumuje się on do kąta pełnego, więc jego miara to \(180^\circ - \alpha\). Wobec tego miara kąta EAD (czyli kąta CAD) jest równa \(180^\circ - (90^\circ + 180^\circ - \alpha) = \alpha - 90^\circ\). Co obliczymy dalej?
Teraz oczywiście znamy miarę kąta środkowego opartego na łuku CD - jest ona równa podwojonej mierze kąta wpisanego opartego na tym łuku, czyli \(2\cdot (\alpha - 90^\circ) = 2\alpha - 180^\circ\). Pozostało tylko wyznaczenie długości łuku...
Jakim ułamkiem kąta pełnego jest kąt środkowy oparty na łuku CD? Ten ułamek to \((2\alpha - 180^\circ): 360^\circ = \frac{\alpha}{180} - \frac{1}{2}\). Długość łuku CD obliczymy, mnożąc długość okręgu przez ten ułamek. Ponieważ długość okręgu jest równa 1, to łuk CD ma długość \(\frac{\alpha}{180} - \frac{1}{2}\).
