Skip to Content

Kąty w okręgu - zadania 1

wt., 09/14/2010 - 18:34 — ciebie

Zaprezentowane rozwiązania są tylko przykładami prawidłowych rozwiązań - większość z zadań można bowiem rozwiązać na wiele sposobów. Zachęcamy Czytelników do podjęcia samodzielnej próby znalezienia własnych metod rozwiązania.

Zadanie 1

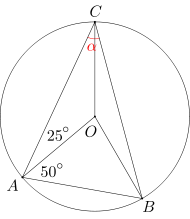
Trójkąt ABC jest wpisany w okrąg o środku O. Wiadomo, że miara kąta BAO wynosi 50 stopni, a miara kąta OAC równa się 25 stopni. Wyznacz miarę kąta ACB.


Wskazówka
Zauważ, że trójkąt ABO jest równoramienny. Wykorzystując tę własność wyznacz najpierw miarę kąta AOB. Kąt ACB jest kątem wpisanym opartym na tym samym łuku co kąt środkowy AOB.


Rozwiązanie
Zauważmy, że AO=BO (oba odcinki są promieniami danego okręgu), a zatem miary kątów ABO i BAO są równe. Stąd wynika, że miara kąta ABO wynosi 50 stopni. Wobec tego miara kata AOB równa się 180-50-50=80 stopni. Kąt ten jest kątem środkowym opartym na łuku AB, a więc kąt ACB - wpisany oparty na tym samym łuku AB - ma miarę 80:2=40 stopni.

Zadanie 2

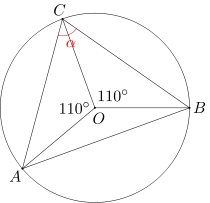
Punkt O jest środkiem okręgu opisanego na trójkącie ABC. Miary kątów AOC i BOC wynoszą po 110 stopni. Wyznacz miarę kąta ACB.


Wskazówka
Wyznacz najpierw miarę kąta środkowego opartego na łuku AB.


Rozwiązanie
Kątem środkowym opartym na łuku AB jest kąt AOB - jego miara wynosi 360-110-110=140 stopni. Kąt ACB jest kątem wpisanym opartym na łuku AB, a więc jego miara jest równa 140:2=70 stopni.

Zadanie 3

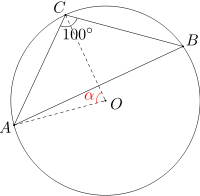
Dany jest trójkąt ABC, w którym AC=BC oraz miara kąta ACB wynosi 100 stopni. Punkt O jest środkiem okręgu opisanego na trójkącie ABC. Wyznacz miarę kąta AOC.


Wskazówka
Kąt AOC jest kątem środkowym oprtym na łuku CA.


Rozwiązanie
Ponieważ trójkąt ABC jest równoramienny, więc miara kąta przy podstawie AB tego trójkąta - czyli miara kąta ABC - wynosi (180-100):2=40 stopni. Kąt ABC jest kątem wpisanym opartym na łuku CA, jego miara jest zatem połową miary kąta AOC (kąt AOC jest kątem środkowym opartym na łuku CA). Stąd wynika, że kąt AOC ma miarę 80 stopni.

Zadanie 4

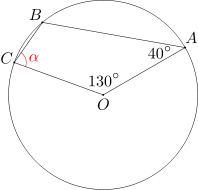
Dany jest czworokąt wypukły ABCO, w którym kąt AOC ma miarę 130 stopni, a kąt OAB ma miarę 40 stopni. Okrąg o środku O przechodzący przez punkt A przechodzi także przez punkty B i C. Wyznacz miarę kąta BCO.


Wskazówka
Wyznacz najpierw miarę kąta ABC - jest to kąt wpisany oparty na łuku CA.


Rozwiązanie
Kąt środkowy oparty na łuku CA ma miarę 360-130=230 stopni. Wobec tego kąt ABC, jako kąt wpisany oparty na (tym samym) łuku CA ma miarę 230:2=115 stopni. A zatem miara kąta przy wierzchołku C czworokąta ABCO wynosi 360-130-40-115=75 stopni.

Zadanie 5

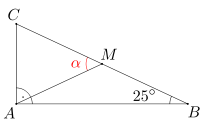
Dany jest trójkąt ABC, w którym kąt BAC jest prosty, a miara kąta ABC wynosi 25 stopni. Punkt M jest środkiem boku BC. Oblicz miarę kąta AMC.


Wskazówka
Opisz okrąg na trójkącie ABC. Wówczas punkt M jest środkiem tego okręgu.


Rozwiązanie

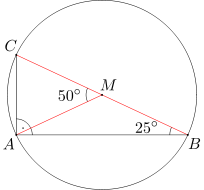
Opiszmy okrąg na trójkącie ABC. Ponieważ kąt BAC jest prosty, więc środkiem tego okręgu jest środek odcinka BC, czyli punkt M. Zatem kąt AMC jest kątem środkowym opartym na łuku CA. Miara kąta AMC jest zatem dwa razy większa od miary kąta ABC (kąt ABC jest kątem wpisanym opartym na łuku CA). Stąd wniosek, że kąt AMC ma miarę 50 stopni.

Zadanie 6

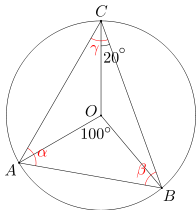
Dany jest trójkąt ABC. Punkt O, leżący wewnątrz tego trójkąta, jest środkiem okręgu opisanego na trójkącie ABC. Miary kątów AOB i OCB wynoszą odpowiednio 100 i 20 stopni. Oblicz miary kątów trójkąta ABC.


Wskazówka
Wyznacz najpierw kąt przy wierzchołku C. Aby wyznaczyć pozostałe kąty uzasadnij, że trójkąty AOB, BOC i COA są równoramienne.


Rozwiązanie
Kąt ACB jest kątem wpisanym opartym na łuku AB, a więc jego miara równa się połowie miary kąta AOB (kąt AOB jest kątem środkowym opartym na łuku AB). Zatem kąt ACB ma miarę 100:2=50 stopni.

Trójkąt OBC jest trójkątem równoramiennym, gdyż odcinki OB i OC są równe promieniowi danego okręgu. Wobec tego kąt OBC ma miarę 20 stopni. Stąd miara kąta BOC wynosi 180-20-20=140 stopni. Ponadto kąt BOC jest kątem środkowym opartym na łuku BC, a więc ma miarę dwukrotnie większą od miary kąta BAC - wpisanego opartego na łuku BC. Zatem miara kąta BAC wynosi 140:2=70 stopni.

Pozostało wyznaczyć miarę kąta ABC: wynosi ona 180-50-70=60 stopni.

Zadanie 7

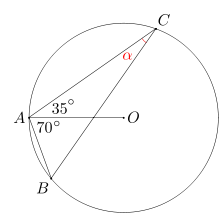
Trójkąt ABC, w którym miara kąta przy wierzchołku A wynosi 105 stopni, jest wpisany w okrąg o środku O. Miara kata CAO równa się 35 stopni. Wyznacz miarę kąta ACB.


Wskazówka
Zauważ, że trójkąt ABO jest trójkątem równoramiennym. Wykorzystaj tę własność do obliczenia miary kąta AOB, który jest kątem środkowym opartym na łuku AB.


Rozwiązanie

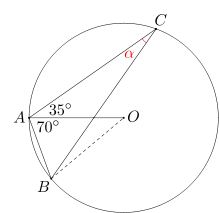
Zauważmy, że AO=BO (oba odcinki są promieniami danego okręgu). Stąd wynika, że trójkąt ABO jest trójkątem równoramiennym, a więc miara kąta ABO wynosi 70 stopni. Wobec tego miara kąta AOB - środkowego opartego na łuku AB - równa się 180-70-70=40 stopni. A zatem miara kąta ACB - wpisanego opartego na łuku AB - wynosi 40:2=20 stopni.

Zadanie 8

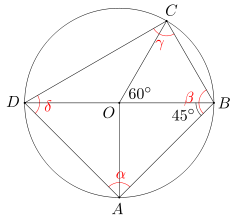
Czworokąt wypukły ABCD jest wpisany w okrąg o środku O. Wiadomo, że punkt O leży na przekątnej BD. Ponadto miara kąta BOC wynosi 60 stopni, a miara kąta ABD równa się 45 stopni. Wyznacz miary kątów czworokąta ABCD.


Wskazówka
Wyznacz najpierw miary kątów przy wierzchołkach A i C. Kąt przy wierzchołku D jest podzielony na dwie części - oblicz miarę każdej z tych części.


Rozwiązanie
Zauważmy, że odcinek BD jest średnicą danego okręgu. A zatem kąty DAB i BCD są kątami wpisanymi opartymi na półokręgach. Stąd wniosek, że miary tych kątów wynoszą po 90 stopni.

Wobec tego miara kąta ADB wynosi 90-45=45 stopni. Ponadto kąt BDC jest kątem wpisanym opartym na łuku BC, a więc jego miara jest równa półowie miary kąta BOC (kąt BOC jest kątem środkowym opartym na łuku BC). Zatem kąt BDC ma miarę 60:2=30 stopni. Ostatecznie, miara kąta ADC równa się 45+30=75 stopni.

Pozostało obliczyć miarę kąta ABC - wynosi ona 360-90-90-75=105 stopni.

Zadanie 9

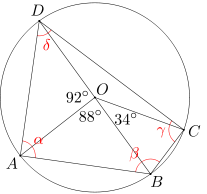
Czworokąt wypukły ABCD jest wpisany w okrąg o środku O. Miary kątów DOA, AOB i BOC wynoszą odpowiednio 92, 88 i 34 stopnie. Wyznacz miary kątów wewnętrznych czworokąta ABCD.


Wskazówka
Każdy z szukanych kątów jest kątem wpisanym opartym na odpowiednim łuku.


Rozwiązanie
Miara kąta COD wynosi 360-92-88-34=146 stopni.

Kąt DAB jest kątem wpisanym opartym na łuku BD, ma więc miarę dwa razy mniejszą od miary kąta środkowego opartego na łuku BD. Wobec tego miara kąta BAD wynosi (34+146)/2=90 stopni.

Analogicznie obliczamy miary pozostałych kątów czworokąta ABCD: Kąt ABC jest kątem wpisanym opartym na łuku CA, ma więc miarę dwa razy mniejszą od miary kąta środkowego opartego na tym samym łuku CA. Stąd miara kąta ABC wynosi (146+92)/2=119 stopni.

Kąt BCD jest kątem wpisanym opartym na łuku DB, ma więc miarę dwa razy mniejszą od miary kąta środkowego opartego na łuku DB. A zatem miara kąta BCD wynosi (92+88)/2=90 stopni.

Pozostało wyznaczyć miarę kąta CDA. Można to zrobić w sposób analogiczny do powyższego, można też wyznaczyć tę miarę wykorzystując miary pozostałych kątów czworokąta ABCD. Ostatecznie miara kąta CDA wynosi 360-90-119-90=61 stopni.

Zadanie 10

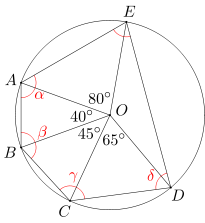
Pięciokąt wypukły ABCDE jest wpisany w okrąg o środku O. Miary kątów EOA, AOB, BOC i COD wynoszą odpowiednio 80, 40, 45 i 65 stopni. Wyznacz miary kątów pięciokąta ABCDE.


Wskazówka
Każdy z kątów danego pięciokąta jest kątem wpisanym opartym na odpowiednim łuku.


Rozwiązanie
Miara kąta DOE wynosi 360-80-40-45-65=130 stopni.

Kąt EAB jest kątem wpisanym opartym na łuku BE, ma więc miarę dwa razy mniejszą od miary kąta środkowego opartego na łuku BE. Wobec tego miara kąta EAB wynosi (45+65+130)/2=120 stopni.

Analogicznie obliczamy miary pozostałych kątów pięciokąta ABCDE. Kąt ABC jest kątem wpisanym opartym na łuku CA, ma więc miarę dwa razy mniejszą od miary kąta środkowego opartego na łuku CA. A zatem miara kąta ABC wynosi (65+130+80)/2=137,5 stopnia.

Kąt BCD jest kątem wpisanym opartym na łuku DB, ma więc miarę dwa razy mniejszą od miary kąta środkowego opartego na łuku DB. Stąd miara kąta BCD wynosi (130+80+40)/2=125 stopni.

Kąt CDE jest kątem wpisanym opartym na łuku EC, ma więc miarę dwa razy mniejszą od miary kąta środkowego opartego na łuku EC. Stąd wynika, że miara kąta CDE wynosi (80+40+45)/2=82,5 stopnia.

Pozostało wyznaczyć miarę kąta DEA. Można to zrobić w sposób analogiczny do powyższego, można też wyznaczyć tę miarę wykorzystując miary pozostałych kątów pięciokąta ABCDE. Wobec tego miara kąta DEA wynosi 540-120-137,5-125-82,5=75 stopni.

Zadanie 11

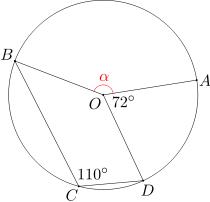
Punkty A, B, C, D leżą na okręgu o środku O w tej właśnie kolejności. Miara kąta BCD wynosi 110 stopni, a miara kąta AOD równa się 72 stopnie. Oblicz miarę kąta AOB.


Wskazówka
Wyznacz najpierw miarę kąta środkowego opartego na łuku DB.


Rozwiązanie
Zauważmy, że kąt BCD jest kątem wpisanym opartym na łuku DB. Zatem kąt wpisany oparty na łuku DB jest dwukroktnie większy od kąta BCD, a więc równa się 220 stopni. Stąd miara kąta AOB wynosi 220-72=148 stopni.

Zadanie 12

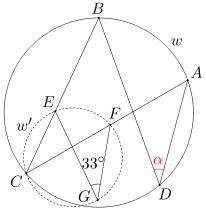
Punkty A, B, C, D leżą na okręgu w w tej właśnie kolejności. Okrąg w' przechodzący przez punkt C przecina odcinki BC i AC odpowiednio w punktach E i F. Punkty F, E, C oraz G leżą na okręgu w' w tej właśnie kolejności. Wiedząc, że miara kąta EGF wynosi 33 stopnie, oblicz miarę kąta ADB.


Wskazówka
Wyznacz najpierw miarę kąta ACB.


Rozwiązanie
Kąty EGF oraz ECF są kątami wpisanymi w okrąg w' opartymi na wspólnym łuku FE, a więc mają równe miary. Stąd wynika, że miara kąta ECF wynosi 33 stopnie. Podobnie kąty ACB i ADB są kątami wpisanymi w okrąg w opartymi na wspólnym łuku AB. Wobec tego miara kąta ADB jest równa mierze kąta ACB i wynosi 33 stopnie.

Zadanie 13

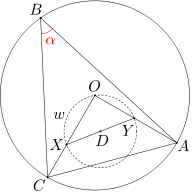
Punkt O jest środkiem okręgu opisanego na trójkącie ostrokątnym ABC. Punkty X, Y leżą na odpowiednio na odcinkach OC i OA. Punkt D jest środkiem odcinka XY. Środek okręgu opisanego na trójkącie OXY pokrywa się z punktem D. Wyznacz miarę kąta ABC.


Wskazówka
Wyznacz najpierw miarę kąta AOC.


Rozwiązanie
Ponieważ środek okręgu opisanego na trójkącie XYO pokrywa się ze środkiem boku XY, więc kąt XOY ma miarę 90 stopni. Kąt AOC ma więc także miarę 90 stopni i ponadto jest kątem środkowym opartym na łuku CA. Wobec tego miara kąta ABC wynosi 90:2=45 stopni.

Zadanie 14

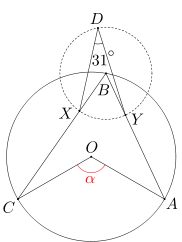
Punkty A, B, C leżą w tej właśnie kolejności na okręgu o środku O. Okrąg w o środku B przecina odcinki BC i AB odpowiednio w punktach X, Y. Punkt D leży na łuku YX okręgu w. Wiedząc, że miara kąta XDY wynosi 31 stopni, oblicz miarę kąta AOC.


Wskazówka
Wyznacz najpierw miarę kąta ABC.


Rozwiązanie
Kąt XBY jest kątem środkowym opartym na łuku XY okręgu w, a zatem jego miara jest dwa razy większa niż miara kąta XDY (kąt XDY jest kątem wpisanym opartym na łuku XY). Wobec tego kąt XBY ma miarę 62 stopnie. Podobnie, kąt AOC jest kątem środkowym opartym na łuku CA, a kąt ABC jest kątem wpisanym opartym na (tym samym) łuku CA. Stąd wniosek, że kąt AOC ma miarę 124 stopnie.



Theme by Dr. Radut.