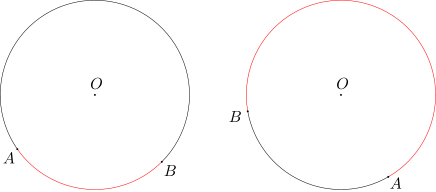
Dany jest okrąg o środku O oraz dwa punkty A i B, leżące na tym okręgu. Łukiem AB danego okręgu nazwiemy fragment tego okręgu biegnący od punktu A do punktu B w kierunku przeciwnym do ruchu wskazówek zegara. Z definicji tej wynika, że łuki AB i BA to dwa różne łuki, które łącznie pokrywają cały okrąg.
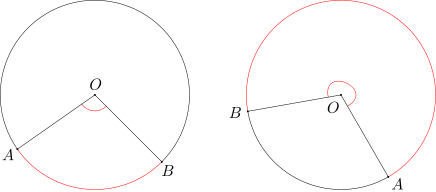
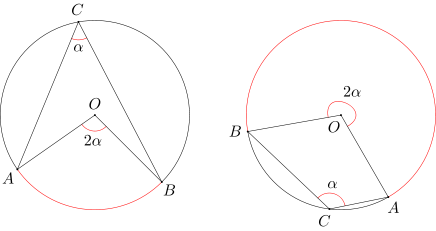
Kątem środkowym opartym na łuku AB nazywamy kąt o wierzchołku O, którego ramionami są półproste OA i OB oraz który zawiera łuk AB w swoim wnętrzu.
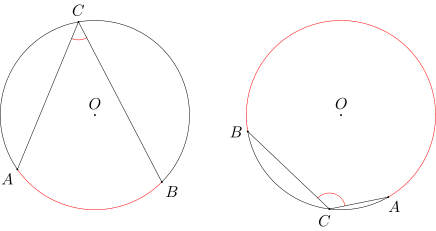
Kątem wpisanym opartym na łuku AB nazywamy kąt ACB, gdzie C jest punktem leżącym na łuku BA, różnym od punktów A i B.
Podstawową zależność wiążącą miarę kąta wpisanego oraz miarę kąta środkowego wyraża następujące twierdzenie:
| Twierdzenie 1: |
|
Miara kąta środkowego opartego na łuku AB jest dwa razy większa od miary dowolnego kąta wpisanego opartego na tym samym łuku AB. |
Z twierdzenia tego płyną następujące wnioski, które często wykorzystujemy w zadaniach.
| Twierdzenie 2: |
|
Miara dowolnego kąta wpisanego opartego na półokręgu wynosi 90 stopni. Również odwrotnie: jeśli kąt wpisany ma miarę 90 stopni, to jest kątem opartym na półokręgu. |
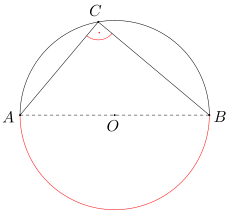
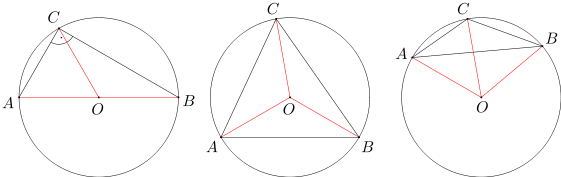
Z twierdzenia 2 wynika w szczególności, że środek okręgu opisanego na trójkącie prostokątnym pokrywa się ze środkiem przeciwprostokątnej. Ponadto nietrudno uzasadnić wykorzystując twierdzenie 1, że środek okręgu opisanego na trójkącie ostrokątnym leży wewnątrz trójkąta, a środek okręgu opisanego na trójkącie rozwartokątnym leży na zewnątrz tego trójkąta.
| Twierdzenie 3: |
|
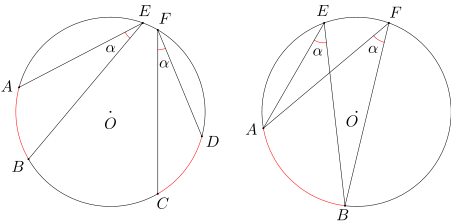
Dane są łuki AB i CD równej długości tego samego okręgu. Wówczas każdy kąt wpisany oparty na łuku AB jest równy każdemu kątowi wpisanemu opartemu na łuku CD. W szczególności każde dwa kąty wpisane oparte na tym samym łuku są równe. |