Zaprezentowane rozwiązania są tylko przykładami prawidłowych rozwiązań - większość z zadań można bowiem rozwiązać na wiele sposobów. Zachęcamy Czytelników do podjęcia samodzielnej próby znalezienia własnych metod rozwiązania.
Zadanie 15
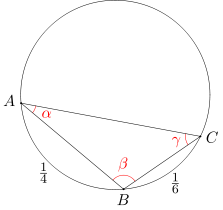
Trójkąt ABC jest wpisany w okrąg o długości 1. Długości łuków AB i BC wynoszą odpowiednio 1/4 i 1/6. Oblicz miary kątów trójkąta ABC.
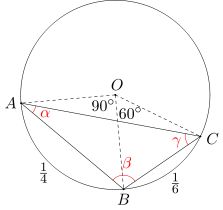
Ponieważ długość łuku AB stanowi 1/4 długości całego okręgu, więc miara kąta AOB wynosi 360:4=90 stopni. Ponadto kąt AOB jest kątem środkowym opartym na łuku AB, a więc ma miarę dwa razy większą od miary kąta ACB (kąt ACB jest kątem wpisanym opartym na łuku AB). A zatem miara kąta ACB wynosi 90:2=45 stopni.
Analogicznie obliczamy miarę kąta BAC. Ponieważ długość łuku BC stanowi 1/6 długości całego okręgu, więc miara kąta BOC wynosi 360:6=60 stopni. Ponadto kąt BOC jest kątem środkowym opartym na łuku BC, a więc ma miarę dwa razy większą od miary kąta BAC (kąt BAC jest kątem wpisanym opartym na łuku BC). A zatem miara kąta BAC wynosi 60:2=30 stopni.
Pozostało wyznaczyć miarę kąta ABC. Miara tego kąta jest równa 180-45-30=105 stopni.
Zadanie 16
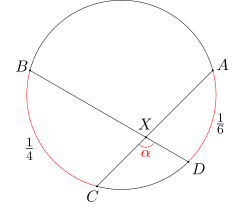
Punkty A, B, C, D leżą w tej właśnie kolejności na jednym okręgu w. Długość łuku BC stanowi 1/4 długości okręgu w. Długość łuku DA stanowi 1/6 długości okręgu w. Cięciwy AC i BD przecinają się w punkcie X. Wyznacz miarę kąta CXD.
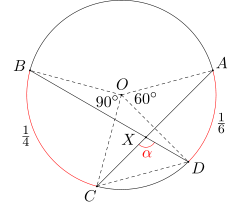
Oznaczmy przez O środek danego okręgu. Ponieważ łuk BC stanowi 1/4 długości danego okręgu, więc miara kąta BOC równa się 360:4=90 stopni. Analogicznie, długość łuku DA stanowi 1/6 długości danego okręgu, więc miara kąta DOA równa się 360:6=60 stopni.
Kąt BDC jest kątem wpisanym opartym na łuku BC, a więc jego miara równa się 90:2=45 stopni. Analogicznie, kąt ACD jest kątem wpisanym opartym na łuku DA, a więc jego miara równa się 60:2=30 stopni.
Wobec tego miara kąta CXD wynosi 180-45-30=105 stopni.
Zadanie 17
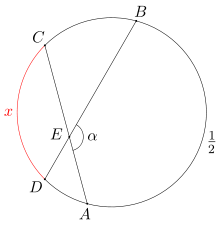
Punkty A, B, C, D leżą w tej właśnie kolejności na okręgu o długości 1. Długość łuku AB wynosi 1/2. Cięciwy AC i BD przecinają się w punkcie E, przy czym miara kąta AEB równa się α. Oblicz długość łuku CD.
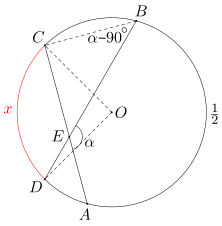
Przyjmijmy, że miara kąta α jest wyrażona w stopniach.
Ponieważ długość łuku AB stanowi 1/2 długości całego okręgu, więc kąt ACB ma miarę 90 stopni (jest to kąt wpisany oparty na półokręgu). Stąd wynika, że miara kąta DBC wynosi
\(180^\circ-\angle BCE-\angle BEC=180^\circ-90^\circ-(180^\circ-\alpha)=\alpha-90^\circ.\)
Oznaczmy przez O środek danego okręgu. Kąt COD jest kątem środkowym opartym na łuku CD, a więc jego miara jest równa
\(2(\alpha-90^\circ)=2\alpha-180^\circ.\)
Stąd wnioskujemy, że długość łuku CD wynosi
\({2\alpha-180^\circ\over 360^\circ}={\alpha\over 180^\circ}- {1\over 2}.\)
Zadanie 18
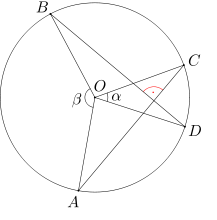
Punkty A, B, C, D leżą w tej właśnie kolejności na okręgu o środku O, przy czym suma miar kątów AOB i COD wynosi 180 stopni. Udowodnij, że cięciwy AC i BD przecinają się pod kątem prostym.
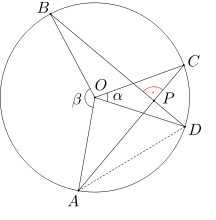
Zauważmy, że kąt CAD jest kątem wpisanym opartym na łuku DC, a zatem jego miara jest równa połowie miary kąta COD. Analogicznie, kąt BDA jest kątem wpisanym opartym na łuku BA, a zatem jego miara jest równa połowie miary kąta AOB. Stąd wynika, że
\(\angle CAD+\angle BDA={1\over2}\angle COD+{1\over2}\angle AOB= {1\over2}\cdot 180^\circ=90^\circ.\)
Wobec tego miara kąta APD wynosi 180-90=90 stopni.
Zadanie 19
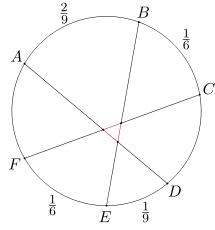
Punkty A, B, C, D, E, F leżą w tej właśnie kolejności na okręgu o długości 1. Długości łuków AB, BC, DE i EF wynoszą odpowiednio 2/9, 1/6, 1/9 i 1/6. Wykaż, że figura ograniczona prostymi AD, BE i CF jest trójkątem równobocznym.
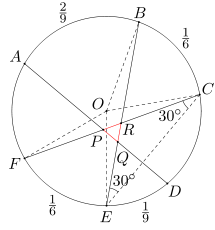
Oznaczmy przez O środek danego okręgu. Ponieważ długość łuku CB stanowi 1/6 długości całego okręgu, więc miara kąta BOC wynosi 360:6=60 stopni. Kąt BOC jest kątem środkowym opartym na łuku CB, a kąt BEC jest kątem wpisanym opartym na (tym samym) łuku CB. A zatem miara kąta BEC wynosi 60:2=30 stopni.
Ponieważ długość łuku FE jest równa długości łuku CB tego samego okręgu, więc miara kąta FCE - wpisanego opartego na łuku FE jest równa mierze kąta wpisanego opartego na łuku CB. Stąd wniosek, że kąt FCE ma miarę 30 stopni. Wobec tego miara kąta PRQ wynosi 30+30=60 stopni.
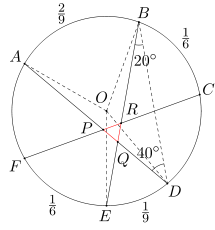
Analogicznie wyznaczamy miarę kąta PQR: Ponieważ długość łuku ED stanowi 1/9 długości całego okręgu, więc miara kąta DOE wynosi 360:9=40 stopni. Kąt DOE jest kątem środkowym opartym na łuku ED, a kąt EBD jest kątem wpisanym opartym na (tym samym) łuku ED. A zatem miara kąta EBD wynosi 40:2=20 stopni.
Podobnie, długość łuku BA stanowi 2/9 długości całego okręgu, więc miara kąta AOB wynosi (2/9)360=80 stopni. Kąt AOB jest kątem środkowym opartym na łuku BA, a kąt ADB jest kątem wpisanym opartym na (tym samym) łuku BA. A zatem miara kąta ADB wynosi 80:2=40 stopni.
W efekcie miara kąta PQR równa się sumie miar kątów EBD i ADB, czyli wynosi 20+40=60 stopni. Trójkąt PQR ma więc dwa kąty równe 60 stopni, jest on zatem trójkątem równobocznym.
Zadanie 20
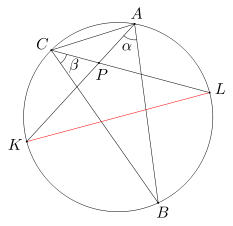
Punkt P leży wewnątrz trójkąta ABC, przy czym suma miar kątów PAB i PCB wynosi 90 stopni. Niech w będzie okręgiem opisanym na trójkącie ABC. Prosta AP przecina okrąg w w punkcie K, a prosta CP przecina okrąg w w punkcie L. Wykaż, że odcinek KL jest średnicą okręgu w.
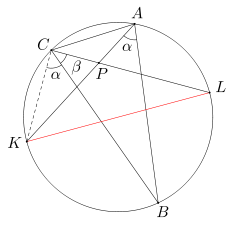
Zauważmy, że kąty KCB i KAB są równe, gdyż są kątami wpisanymi opartymi na tym samym łuku KB. Wobec tego suma miar kątów KCB i BCL - czyli miara kąta KCL - wynosi 90 stopni. Stąd wynika, że łuk KL jest półokręgiem, a zatem odcinek KL jest średnicą okręgu w.
Zadanie 21
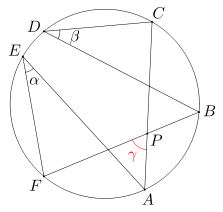
Punkty A, B, C, D, E, F leżą w tej właśnie kolejności na jednym okręgu. Cięciwy AC i BF przecinają się w punkcie P. Wiedząc, że miary kątów FEA i BDC wynoszą odpowiednio α i β, oblicz miarę kąta APF.
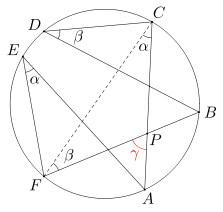
Miara kąta FCA jest równa α, gdyż kąt ten jest kątem wpisanym opartym na tym samym łuku co kąt FEA. Analogicznie, miara kąta BFC jest równa β, gdyż kąt ten jest kątem wpisanym opartym na tym samym łuku co kąt BDC. Wobec tego miara kąta APF wynosi α + β.
Zadanie 22
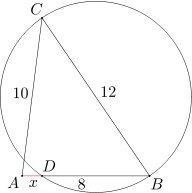
Dany jest trójkąt ABC, w którym długości boków AB, BC i CA wynoszą odpowiednio 8, 12 i 10. Okrąg o średnicy BC przecina odcinek AB w punkcie D. Oblicz długości odcinka AD.
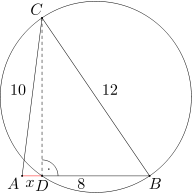
Ponieważ odcinek BC jest średnicą danego okręgu, więc kąt BDC jest kątem wpisanym opartym na półokręgu. Stąd wynika, że miara kąta BDC wynosi 90 stopni.
Do wyznaczenia długości odcinka AD wykorzystamy twierdzenie Pitagorasa.
Oznaczmy przez x długość odcinka AD. Wówczas długość odcinka BD równa się 8-x. Stąd na mocy twierdzenia Pitagorasa dostajemy
AC2 − AD2 = CD2 = BC2 − BD2.
Stąd dostajemy równanie
100 − x2 = 144 − (8 − x)2,
z którego wyznaczamy x=5/4. A zatem długość odcinka AD wynosi 5/4.
Zadanie 23
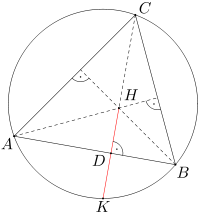
Punkt H jest punktem przecięcia wysokości trójkąta ostrokątnego ABC. Prosta CH przecina okrąg opisany na trójkącie ABC w punkcie K. Proste AB i CH przecinają się w punkcie D. Wykaż, że punkt D jest środkiem odcinka HK.
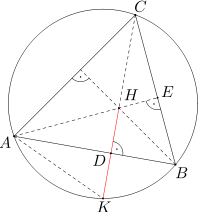
Oznaczmy przez E punkt przecięcia prostych AH i BC. Wówczas trójkąty AEB i CDB są prostokątne i mają wspólny kąt przy wierzchołku B. Stąd wynika, że
\(\angle HAD=90^\circ-\angle ABC=\angle KCB.\)
Ponadto kąty KAB i KCB są równe, gdyż są to kąty wpisane oparte na tym samym łuku KB. Stąd wniosek, że kąty KAD i HAD są równe. Ponadto oba kąty ADK i ADH są proste, a odcinek AD jest wspólnym bokiem trójkątów ADK i ADH. Wobec tego trójkąty ADH i ADK są przystające (cecha kąt-bok-kąt), skąd bezpośrednio wynika równość odcinków HD i KD.
Zadanie 24
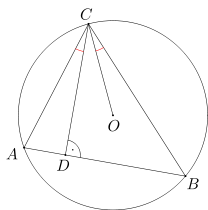
Punkt O jest środkiem okręgu opisanego na trójkącie ostrokątnym ABC. Punkt D jest rzutem prostokątnym punktu C na bok AB. Wykaż, że kąty ACD i BCO są równe.
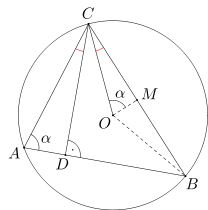
Oznaczmy przez M środek boku BC. Ponieważ trójkąt BCO jest trójkątem równoramiennym, więc odcinek OM jest wysokością w trójkącie BCO. Odcinek OM jest również zawarty w dwusiecznej kąta BOC. Stąd wynika, że
\(\angle DAC={1\over 2}\angle BOC=\angle MOC.\)
Wobec tego
\(\angle ACD=90^\circ-\angle DAC=90^\circ-\angle MOC=\angle BCO.\)
Zadanie 25
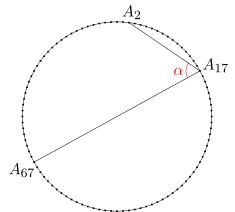
Dany jest 100-kąt foremny A1A2...A100. Oblicz miarę kąta A2A17A67.
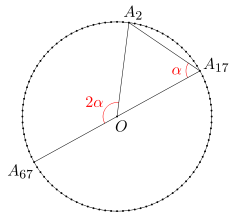
Na danym 100-kącie foremnym opiszmy okrąg. Wówczas kąt A2A17A67 jest kątem wpisanym opartym na łuku A2A67. Ponadto kąt środkowy oparty na łuku A2A67 ma miarę
\({100-67+2\over 100}\cdot 360^\circ=126^\circ.\)
Stąd otrzymujemy, że miara kąta A2A17A67 równa się 126:2=63 stopnie.
Zadanie 26
Czy istnieje 100 punktów na płaszczyżnie o tej własności, że żadne trzy spośród tych punktów nie leżą na jednej prostej oraz każdy trójkąt o wierzchołkach w tych punktach jest trójkątem rozwartokątnym.
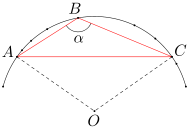
Takich 100 punktów istnieje. Rozpatrzmy okrąg oraz wybierzmy na nim taki łuk l, który jest krótszy od połowy długości tego okręgu. Wówczas dowolnych 100 punktów leżących na łuku l spełnia warunki zadania.
Istotnie: niech A, B, C będą dowolnymi punktami leżącymi w tej właśnie kolejności na łuku l. Wówczas kąt ABC jest kątem wpisanym, opartym na łuku AC. Ponieważ łuk AC jest dłuższy od połowy okręgu, więc kąt środkowy oparty na łuku AC ma miarę większą od 180 stopni. Wobec tego kąt ABC ma miarę większą od 180:2=90 stopni, co oznacza, że trójkąt ABC jest rozwartokątny.
Zadanie 27
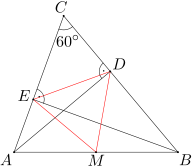
Dany jest trójkąt ostrokątny ABC, w którym miara kąta ACB wynosi 60 stopni. Punkty D i E są spodkami wysokości tego trójkąta poprowadzonymi odpowiednio z wierzchołków A i B. Punkt M jest środkiem boku AB. Udowodnij, że trójkąt DEM jest równoboczny.
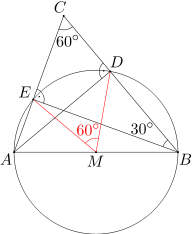
Rozpatrzmy okrąg o średnicy AB. Ponieważ kąty AEB i ADB są proste, więc okrąg ten przechodzi przez punkty D i E. Ponadto punkt M jest środkiem tego okręgu. Stąd wynika, że DM=EM. Zatem aby wykazać, że trójkąt DEM jest równoboczny, wystarczy udowodnić, że miara kąta DME wynosi 60 stopni.
Kąt EMD jest kątem środkowym opartym na łuku DE, a zatem jego miara jest dwa razy większa od miary kąta EBC. Wobec tego
\(\angle EMD=2\angle EBD=2(90^\circ-\angle ACB)= 2\cdot 30^\circ=60^\circ.\)
Stąd oraz z równości DM=EM wynika, że trójkąt DEM jest równoboczny.
Zadanie 28
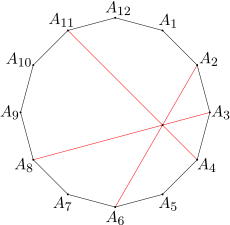
Udowodnij, że w 12-kącie foremnym A1A2...A12 przekątne A2A6, A3A8, A4A11 przecinają się w jednym punkcie.
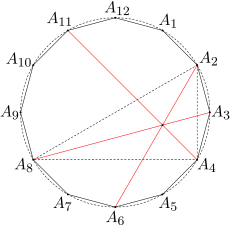
Opiszmy okrąg na danym 12-kącie. Wówczas długości łuków A2A11 i A11A8 są równe, długości łuków A8A6 i A6A4 są równe oraz długości łuków A4A3 i A3A2 są równe. Stąd wynika, że rozpatrywane przekątne są zawarte w dwusiecznych kątów wewnętrznych trójkąta A2A4A8. Wobec tego przekątne te przecinają się w jednym punkcie.
