Skip to Content

Okręgi styczne

strict warning: Only variables should be passed by reference in /var/www/uczesie/modules/book/book.module on line 560.
śr., 09/15/2010 - 10:04 — ciebie

Dwa okręgi nazywamy stycznymi, jeśli okręgi te mają dokładnie jeden punkt wspólny. Punkt wspólny obu tych okręgów nazywamy punktem styczności okręgów.

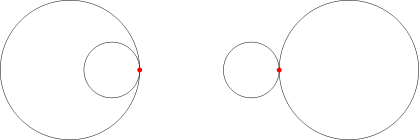
Wyróżniamy dwa rodzaje okręgów stycznych. Mówimy, że okręgi są styczne wewnętrznie, jeśli są styczne oraz jeden z nich leży wewnątrz drugiego. Jeśli z kolei dwa okręgi są styczne i żaden z nich nie leży wewnątrz drugiego, to mówimy, że okręgi te są styczne zewnętrznie.

Twierdzenie 1:

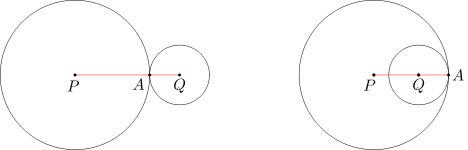
Dane są okręgi o środkach P, Q, które są styczne w punkcie A. Wówczas punkty P, Q oraz A leżą na jednej prostej. Ponadto, jeśli okręgi są styczne zewnętrznie, to długość odcinka PQ jest równa sumie promieni tych okręgów, natomiast jeśli okręgi są styczne wewnętrznie, to długość odcinka PQ jest równa wartości bezwzględnej różnicy długości promieni tych okręgów.


Dlaczego tak jest?
Zwróćmy uwagę na symetrię rysunku względem prostej PQ. Ponieważ przechodzi ona przez środki okręgów, to dzieli je na połowy. Gdyby punkt A leżał pod prostą PQ, to ponieważ nad prostą ryzunek wygląda tak samo, jak pod nią, nad prostą musiałby się znajdować drugi punkt, w którym okręgi byłyby styczne. A to, jak wiemy, niemożliwe. Tak samo niemożliwa jest sytuacja, w której punkt A leży nad prostą PQ. Wobec tego musi leżeć na tej prostej.



Theme by Dr. Radut.