Głównym narzędziem przydatnym w zadaniach z tego działu jest oczywiście Twierdzenie 1, które tłumaczy warunek styczności okręgów (mają dokładnie jeden punkt wspólny) na warunki mówiące coś o położeniu punktów i odległościach, dużo łatwiejsze do wykorzystania w zadaniach. Bardzo często będziemy korzystać z tego, że środki okręgów stycznych wyznaczają prostą, na której leży także punkt styczności. Wynikający stąd warunek na odległość pomiędzy środkami okręgów stycznych także się przydaje w ciekawej grupie zadań, do której należą przykłady 2 i 3.
Przy zadaniach o okręgach stycznych nie można zapomnieć, co wiemy o styczności między okręgiem a prostą. Chociażby dlatego, że jeśli dwa okręgi są styczne, to mają wspólną prostą styczną przechodzącą przez punkt ich styczności. Często warto tę wspólną prostą styczną dorysować. Następnym krokiem może być zaznaczenie na rysunku kątów prostych, które pojawiają się przy prostych stycznych do okręgów (między stycznymi a promieniami). Dobrze ilustruje to przykład 4 (zadanie 9).
Warto pamiętać, że wspólna styczna do dwóch stycznych okręgów, przechodząca przez ich punkt styczności, jest prostopadła do prostej łączącej środki. Wynika to z faktu, że jest ona prostopadła do promieni kończących się w punkcie styczności.
Zaczniemy od prostego przykładu, który pokaże, jak używać w zadaniach Twierdzenia 1.
Przykład 1 (Zadanie 2)
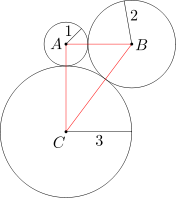
Dane są trzy okręgi o środkach A, B, C oraz odpowiednio promieniach długości 1, 2, 3. Każdy z tych okręgów jest styczny zewnętrznie do obu pozostałych. Oblicz pole trójkąta ABC.
Rozwiązanie
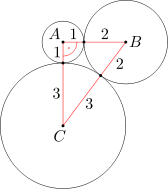
Zanim zaczniemy się zastanawiać, jak obliczyć pole trójkąta ABC, pomyślmy, jakie informacje o tym trójkącie możemy wyciągnąć z danych zadania. W jaki sposób może nam pomóc to, że dane okręgi są styczne? Z twierdzenia 1 wynika, że odpowiednie punkty styczności leżą na odcinkach AB, AC i BC, a te odcinki są sumami odpowiednich promieni: |AB| = 1+2 = 3, |AC| = 1 + 3 = 4, |BC| = 2+3 = 5. Znamy długości boków trójkąta ABC, czyli tak naprawdę możemy już zapomnieć o okręgach z treści zadania, ponieważ umiemy narysować trójką ABC bez nich, wykorzystując informacje o długościach boków.
Pozostaje więc zadanie obliczenia pola trójkąta o bokach długości 3, 4, 5. W całkiem dowolnym trójkącie mogłoby być trudno obliczyć pole, mając tylko długości boków, ale okazuje się, że ten trójkąt jest specyficzny... Długości jego boków spełniają warunek z twierdzenia Pitagorasa: 3^2 + 4^2 = 9 + 16 = 25 = 5^2. Wobec tego ABC jest trójkątem prostokątnym! W tej sytuacji łatwo obliczyć pole. Wystarczy wymnożyć długości przyprostokątnych i podzielić przez dwa. Ponieważ przeciwprostokątną jest najdłuższy bok, to przyprostokątne mają długości 3 i 4, a pole trójkąta ABC jest równe 3*4/2 = 6.
Celem zaprezentowanej poniżej ciekawej grupy zadań jest wyznaczenie promienia okręgu lub okręgów umieszczonych w większej figurze, stycznych w jakiejś konfiguracji do jej boków. Jak się za to zabrać? Ogólna wskazówka brzmi narysuj wspólny promień. Żeby jakoś powiązać szukaną długość promienia z danymi, najlepiej umieścić je na jednym odcinku - wtedy łatwo będzie je porównać i ułożyć jakieś równania. Szczegóły tej metody wyjaśnione w przykładach powinny pomóc rozwiązywać podobne zadania.
Przykład 2 (Zadanie 3)
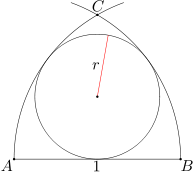
Dane są punkty A, B o odległości 1. Okrąg o środku A i promieniu 1 przecina okrąg o środku B i promieniu 1 w punkcie C (zob. rysunek). W figurę ograniczoną odcinkiem AB oraz łukami BC i CA rozpatrywanych okręgów wpisano okrąg o promieniu r. Oblicz r.
Rozwiązanie
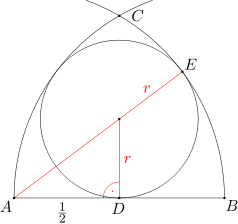
Żeby obliczyć promień r małego okręgu, zastanówmy się, w jaki sposób porównać go z promieniem któregoś z większych okręgów. Jeśli oba promienie umieścimy na jednej prostej, to może uda się przedstawić dłuższy jako sumę krótszego i czegoś, co znamy lub co łatwo obliczyć...Okazuje się, że tak dobrze nie jest, ale właściwie niewiele brakuje. Zaczynamy więc od narysowania prostej przechodzącej przez środek małego okręgu, który oznaczymy przez O, i środek któregoś z dużych okręgów - niech będzie A. Ponadto oznaczmy przez D punkt styczności małego okręgu z odcinkiem AB (jest to jego środek - czy umiesz wyjaśnić dlaczego?), a przez E jego punkt styczności z dużym okręgiem o środku w punkcie A.
Z Twierdzenia 1 wynika, że punkty A, O i E są współliniowe. Odcinek OE to promień małego okręgu, czyli jego długość to r. Ponieważ odcinek AE jest promieniem dużego okręgu, czyli ma długość 1, to długość odcinka AO wynosi 1-r. Popatrzmy na rysunek i poszukajmy innego sposobu wyrażenia długości odcinka AO lub OE, aby otrzymać jakieś równanie na r.
Taki sposób może nam dostarczyć trójkąt ADO. Jest on prostokątny, ponieważ odcinek AB jest styczny do małego okręgu w punkcie D, czyli promień OD jest prostopadły do odcinka AD. Co więcej, znamy długości obu przyprostokątnych! Bok OD jest promieniem małego okręgu, czyli ma długość r, natomiast punkt D jest środkiem odcinka AB, więc bok AD ma długość 1/2. Korzystając z twierdzenia Pitagorasa możemy zapisać AO2 = AD2 + OD2 = 1 / 4 + r2, czyli \(AO = \sqrt{1/4 + r^2}\). Wobec tego mamy już dwa opisy długości odcinka AO, z których otrzymujemy równanie
\(1-r = \sqrt{1/4 + r^2}\),
które przekształcamy do postaci (1 − r)2 = 1 / 4 + r2
i dalej 1 − 2r + r2 = 1 / 4 + r2,
a stąd po przeniesieniu wyrazów na odpowiednie strony 2r = 3 / 4,
czyli ostatecznie r = 3 / 8.
Kolejne zadanie jest oparte na tej samej metodzie, ale trochę trudniejsze - można przeczytać opis rozwiązania lub spróbować zastosować do niego powyższą metodę samodzielnie, pomagając sobie kolejnymi wskazówkami.
Przykład 3 (Zadanie 4)
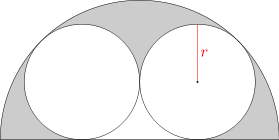
Dwa okręgi o promieniu r są styczne zewnętrznie i wpisane w półkole o promieniu 1, jak pokazano na rysunku. Oblicz r oraz pole zacieniowanego fragmentu.
Rozwiązanie
Po pierwsze, jest to trójkąt prostokątny - kąt ODP jest prosty, ponieważ odcinek OD jest styczny do okręgu o środku P w punkcie D.
Po drugie, bok PD jest promieniem okręgu, więc ma długość r.
Jak wyznaczyć długość boku OP?
Stąd długość odcinka OD jest równa r.
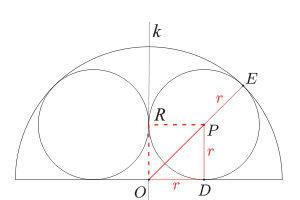
Odcinek OE jest promieniem półkola, więc ma długość 1. Odcinek SE jest promieniem jednego z okręgów, więc jego długość to szukana liczba r. Wobec tego odcinek OP ma długość 1-r. Teraz chcielibyśmy opisać któryś z odcinków, którego długość jest zależna od r, w inny sposób, aby otrzymać równanie, z którego wyznaczymy r.
Niech D oznacza punkt styczności okręgu o środku P ze średnicą półkola. Co możemy powiedzieć o trójkącie OPD?
Jednym z boków trójkąta OPD jest odcinek OP, który chcielibyśmy opisać w inny sposób, niż jako różnicę odcinków OE i PE. Być może uda się to, jeśli dowiemy się więcej o tym trójkącie.
Po pierwsze, jest to trójkąt prostokątny - kąt ODP jest prosty, ponieważ odcinek OD jest styczny do okręgu o środku P w punkcie D.
Po drugie, bok PD jest promieniem okręgu, więc ma długość r.
Jak wyznaczyć długość boku OP?
Zauważmy, że ponieważ okręgi wpisane w półkole są identyczne, to rysunek musi być symetryczny względem prostej k przechodzącej przez punkt O i prostopadłej do średnicy półkola. Oznaczmy przez R punkt styczności okręgu o środku S z prostą k. Odcinek PR jest promieniem, więc ma długość r. Co wiadomo o czworokącie ODPR?
Wykażemy, że czworokąt ODPR jest kwadratem. Kąt DOR jest prosty, ponieważ prostą k narysowaliśmy jako prostopadłą do średnicy półkola, natomiast kąty ODP i ORP są proste jako kąty między stycznymi a promieniami do punktów styczności. Wobec tego ten czworokąt jest prostokątem. Ale sąsiednie boki PD i PR to promienie okręgu, więc wszystkie boki są równe.
Stąd długość odcinka OD jest równa r.
Możemy wrócić do trójkąta ODP. Skorzystamy z twierdzenia Pitagorasa: OP2 = OD2 + PD2 = 2r2, więc \(OP = r\sqrt{2}\). Ale z drugiej strony wiemy, że odcinek OP ma długość 1-r, więc otrzymujemy równanie \(1-r = r\sqrt{2}\). A stąd ostatecznie \(r = 1/(1+\sqrt{2}) = \sqrt{2} - 1\).
Teraz możemy obliczyć pole zacieniowanej części figury. W tym celu możemy obliczyć pole białej części i odjąć je od pola półkola. Biała część składa się z dwóch figur symetrycznych względem prostej k. Popatrzmy na prawą część: co z niej zostanie, jak wyrzucimy kwadrat ODPR?
Prawa połowa białej części półkola to suma kwadratu ODPR i trzech czwartych okręgu. Wobec tego jej pole to \(r^2 + 3/4\cdot \pi r^2\). Wobec tego pole całej białej figury to \(2(r^2 + 3/4\cdot \pi r^2) = r^2(2 + 3/2\pi)\), a pole zacieniowanej części jest równe π / 2 − r2(2 + 3 / 2π).
Na koniec ciekawe zadanie, które pokazuje, że dorysowanie wspólnej prostej stycznej w punkcie styczności pary okręgów może bardzo uprościć rozwiązanie problemu.
Przykład 4 (Zadanie 9)
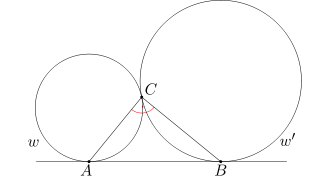
Okręgi w oraz w' są styczne zewnętrznie w punkcie C. Do okręgów tych poprowadzono wspólną styczną zewnętrzną AB (punkty A i B są punktami styczności tej stycznej odpowiednio z okręgami w i w'. Udowodnij, że kąt ACB jest kątem prostym.
Uwaga Jeśli przyszedł nam do głowy pomysł narysowania wspólnej stycznej od danych okręgów, przechodzącej przez ich punkt styczności, to jesteśmy na dobrej drodze do wymyślenia eleganckiego rozwiązania (zobacz Rozwiązane 1). Jeśli nie, to nadal mamy szansę zrobić to zadanie, chociaż może trochę dłuższą i bardziej rachunkową drogą (zobacz Rozwiązanie 2).
Rozwiązanie 1.
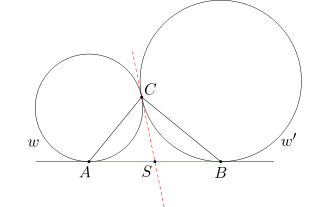
Rysujemy wspólną styczną do danych okręgów, przechodzącą przez punkt C. Niech S oznacza punkt jej przecięcia z odcinkiem AB. Popatrzmy najpierw na trójkąt ASC. Punkty A i C są punktami styczności prostych SA i SC z okręgiem w, więc odcinki SA i SC są równe. Wobec tego trójkąt ASC jest równoramienny - kąty SAC i SCA mają tę samą miarę α. Tak samo trójkąt BSC jest równoramienny - kąty SBC i SCB mają tę samą miarę β.
Teraz przyjrzyjmy się kątom trójkąta ABC. Miary kątów CAB i CBA wynoszą odpowiednio α i β, natomiast miara kąta ACB to suma miar kątów ACS i BCS, czyli jest równa α + β. Możemy więc zapisać równość \(180^\circ = \alpha + \beta + (\alpha + \beta) = 2(\alpha + \beta)\). A stąd \(\alpha + \beta = 90^\circ\). Ale α + β to właśnie miara kąta ACB!
Rozwiązanie 2.
Jeśli nie pomyśleliśmy o dorysowaniu wspólnej stycznej, to spróbujmy wykonać kilka prostych rachunków. Oznaczmy przez α miarę kąta CAB, a przez β miarę kąta CBA. Chcielibyśmy wykazać, że ich suma to 90 stopni - jeśli tak jest, to miara kąta ACB również wynosi 90 stopni, jako dopełnienie do 180 stopni.
Skorzystamy z twierdzenia o kącie między styczną a cięciwą. Kąt CAB to kąt pomiędzy styczną do okręgu w w punkcie A i cięciwą AS. Wobec tego dowolny kąt wpisany w okrąg w i oparty na łuku AS ma tę samą miarę, co kąt CAB, a kąt środkowy oparty na tym łuku ma miarę dwa razy większą. Stąd, jeśli przez X oznaczymy środek okręgu w, miara kąta AXC wynosi 2α. Analogiczny rachunek wykazuje, że jeśli Y oznacza środek okręgu w', to miara kąta BYC jest równa 2β.
Teraz skorzystamy z Twierdzenia 1, żeby stwierdzić, że punkt C leży na odcinku XY, czyli kąty AXC i BYC są kątami czworokąta ABYX. Pozostałe dwa kąty w tym czworokącie są proste, jako kąty pomiędzy stycznymi a promieniami poprowadzonymi do punktów styczności. Suma kątów czworokąta ABXY jest więc równa \(2\alpha + 2\beta + 2\cdot 90^\circ\). Oczywiście ta suma to 360 stopni - stąd obliczamy łatwo, że, tak jak chcemy, \(\alpha + \beta = 90^\circ\).
