Zaprezentowane rozwiązania są tylko przykładami prawidłowych rozwiązań - większość z zadań można bowiem rozwiązać na wiele sposobów. Zachęcamy Czytelników do podjęcia samodzielnej próby znalezienia własnych metod rozwiązania.
Zadanie 1
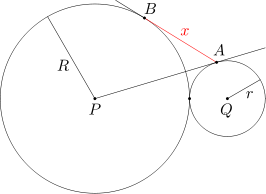
Okrąg w o środku P i promieniu R jest styczny zewnętrznie do okręgu w' o środku Q i promieniu r. Prosta przechodząca przez punkt P jest styczna do okręgu w' w punkcie A. Prosta przechodząca przez punkt A jest styczna do okręgu w w punkcie B. Oblicz długość odcinka AB.
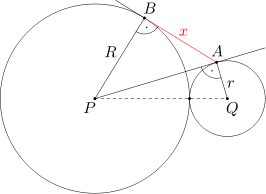
Ponieważ prosta PA jest styczna do okręgu w' w punkcie A, więc kąt PAQ jest kątem prostym. Analogicznie, prosta AB jest styczna do okręgu w w punkcie B, więc kąt ABP jest kątem prostym. Stąd korzystając z twierdzenia Pitagorasa otrzymujemy
PQ2 = PA2 + AQ2 oraz PA2 = PB2 + AB2.
Stąd otrzymujemy:
PQ2 = PB2 + AB2 + AQ2,
Ponieważ dane okręgi są styczne zewnętrznie, więc długość odcinka PQ jest równa sumie promieni tych okręgów. A zatem otrzymujemy równość
(R + r)2 = R2 + AB2 + r2,
skąd bezpośrednio obliczamy długość odcinka AB:
\(AB=\sqrt{2Rr}.\)
Zadanie 2
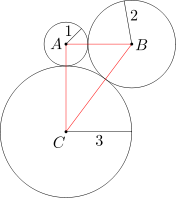
Dane są trzy okręgi o środkach A, B, C oraz odpowiednio promieniach długości 1, 2, 3. Każdy z tych okręgów jest styczny zewnętrznie do obu pozostałych. Oblicz pole trójkąta ABC.
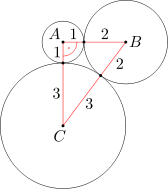
Ponieważ dane okręgi o środkach A i B są styczne zewnętrznie, więc długość odcinka AB jest równa sumie długości promieni tych okręgów. A zatem długość odcinka AB wynosi 1+2=3. Analogicznie wyznaczamy długości odcinków BC oraz CA: Długość odcinka BC równa się 2+3=5, a długość odcinka CA wynosi 3+1=4.
A zatem długości boków trójkąta ABC wynoszą odpowiednio 3, 4, 5. Ponieważ 32 + 42 = 52, więc korzystając z twierdzenia odwrotnego do twierdzenia Pitagorasa wnioskujemy, że trójkąt ABC jest prostokątny, a kąt prosty znajduje się przy wierzchołku A.
Wobec tego pole trójkąta ABC równa się 6.
Zadanie 3
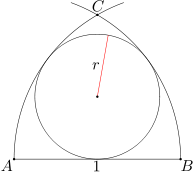
Dane są punkty A, B o odległości 1. Okrąg o środku A i promieniu 1 przecina okrąg o środku B i promieniu 1 w punkcie C (zob. rysunek). W figurę ograniczoną odcinkiem AB oraz łukami BC i CA rozpatrywanych okregów wpisano okrag o promieniu r. Oblicz r.
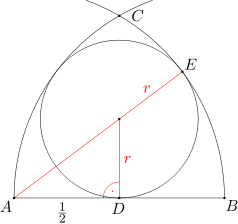
Oznaczmy przez O środek okręgu o promieniu r, a przez D punkt styczności okręgu o promieniu r z odcinkiem AB. Wówczas punkt D jest środkiem odcinka AB oraz kąt ADO jest prosty.
Niech ponadto E będzie punktem styczności okręgu o promieniu r z łukiem BC. Wówczas punkty A, O, E leżą na jednej prostej. Odcinek AE ma długość 1, a odcinek OE ma długość r. Wobec tego odcinek AO ma długość 1-r.
Zatem wykorzystując twierdzenie Pitagorasa dla trójkąta ADO otrzymujemy:
AD2 + OD2 = AO2
Stąd dostajemy równanie
(1 / 2)2 + r2 = (1 − r)2.
Rozwiązując je otrzymujemy r=3/8.
Zadanie 4
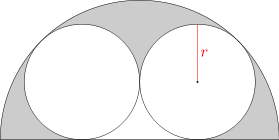
Dwa okręgi o promieniu r są styczne zewnętrznie i wpisane w półkole o promieniu 1, jak pokazano na rysunku. Oblicz r oraz pole zacieniowanego fragmentu.
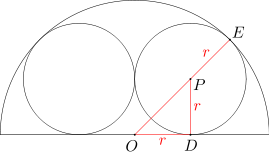
Niech O będzie środkiem danego półkola, P środkiem jednego z danych okręgów o promieniu r. Niech ponadto D będzie punktem styczności okręgu o środku P i promieniu r ze średnicą półokręgu. Wówczas długość odcinka OD jest równa r.
Oznaczmy ponadto przez E punkt styczności okręgu o środku P i promieniu r z danym półokręgiem. Wówczas punkty O, P, E leżą na jednej prostej. Długość odcinka OE wynosi 1 (jest to promień danego półokręgu), a długość odcinka PE równa się r. Wobec tego długość odcinka OP równa się 1-r.
Wykorzystując twierdzenie Pitagorasa do trójkąta ODP otrzymujemy:
OD2 + DP2 = OP2.
Stąd dostajemy
2r2 = (1 − r)2.
Ponieważ liczby r oraz 1-r są dodatnie, więc możemy wyciągnąć pierwsiatek kwadratowy z obu stron otrzymując
\(r\sqrt2=1-r.\)
Stąd po przekształceniach uzyskujemy:
\(r=\sqrt2-1.\)
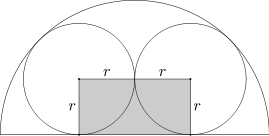
Aby obliczyć pole danego obszaru zauważmy, że obszar ten powstaje poprzez usunięcie z półkola zacieniowanego prostokąta (o bokach r i 2r) oraz dwóch 3/4 okręgów o promieniu r. Wobec tego szukane pole wynosi:
\({1\over2}\pi\cdot 1^2-2r^2-2\cdot {3\over4}\pi r^2= {1\over2}\pi-\Bigl(2+{3\over2}\pi\Bigr) r^2= {1\over2}\pi-\Bigl(2+{3\over2}\pi\Bigr)(\sqrt2-1)^2.\)
Zadanie 5
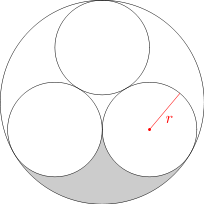
Trzy okręgi o promieniu r są styczne zewnętrznie i wpisane w koło o promieniu 1, jak pokazano na rysunku. Oblicz r oraz pole zacieniowanego fragmentu.
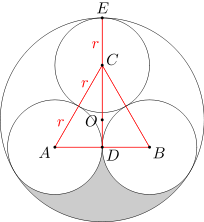
Oznaczmy przez A, B, C środki danych okręgów o promieniu r. Niech ponadto O będzie środkiem danego koła o promieniu 1, a D punktem styczności danych okręgów o środkach A i B. Wówczas trójkąt ABC jest równoboczny, punkt D jest środkiem odcinka AB, a punkt O jest środkiem trójkąta ABC.
Oznaczmy przez E punkt styczności okręgów o środkach C i O. Wówczas punkty O, C, E leżą na jednej prostej. Ponadto długość odcinka CE wynosi r, a długość odcinka OE wynosi 1. Wobec tego długość odcinka OC wynosi 1-r.
Ponieważ punkt O jest środkiem trójkąta równobocznego ABC, więc długość odcinka OC jest równa 2/3 długości odcinka CD. Stąd wynika, że długość odcinka CD wynosi 3(1-r)/2.
Korzystając z twierdzenia Pitagorasa dla trójkąta prostokątnego ADC dostajemy
AD2 + CD2 = AC2.
Stąd dostajemy równanie
\(r^2+{9(1-r)^2\over 4}=4r^2.\)
Mnożąc stronami przez 4 oraz grupując wyrazy podobne uzyskujemy
3(1 − r)2 = 4r2.
Ponieważ zarówno r jak i 1-r są liczbami dodatnimi, więc możemy wyciągnąć pierwiastek kwadratowy z obu stron powyższej równości otrzymując
\((1-r)\sqrt3=2r.\)
Stąd po kilku przekształceniach wyznaczmy r:
\(r=2\sqrt3-3.\)
Niech S oznacza pole szukanego obszaru. Usuwając z danego koła o środku O i promieniu 1 trójkąt równoboczny ABC oraz trzy kawałki, z których każdy równa się 5/6 części okręgu o promieniu r, uzyskujemy obszar, którego pole równa się 3S. A zatem
\(3S=\pi\cdot 1^2-{(2r)^2\sqrt3\over 4}-3\cdot {5\over 6}\pi r^2= \pi-\Bigl(\sqrt3+{5\over2}\pi\Bigr)r^2= \pi-\Bigl(\sqrt3+{5\over2}\pi\Bigr)(2\sqrt3-3)^2. \)
Wobec tego ostatecznie
\(S={\pi\over 3}-\Bigl({\sqrt3\over 3}+{5\over6}\pi\Bigr)(2\sqrt3-3)^2. \)
Zadanie 6
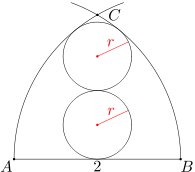
Dane są punkty A, B o odległości 2. Okrąg o środku A i promieniu 2 przecina okrąg o środku B i promieniu 2 w punkcie C (zob. rysunek). W figurę ograniczoną odcinkiem AB oraz łukami BC i CA rozpatrywanych okręgów wpisano dwa okręgi styczne zewnętrznie, każdy o promieniu r, jak pokazano na rysunku. Oblicz r.
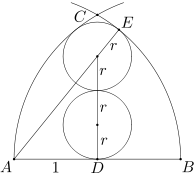
Oznaczmy przez O środek górnego okręgu, a przez D punkt styczności dolnego okręgu z odcinkiem AB. Wówczas punkt D jest środkiem odcinka AB. Ponadto odcinek OD ma długość 3r.
Niech E będzie punktem styczności górnego okręgu z łukiem BC. Wówczas punkty A, O, E leżą na jednej prostej. Ponadto długość odcinka AE wynosi 2 (jest to promień danego łuku o środku A), a długość odcinka OE równa się r. Stąd wniosek, że długość odcinka AO wynosi 2-r.
Wykorzystując twierdzenia Pitagorasa dla trójkąta ADO uzyskujemy
AD2 + DO2 = AO2.
Stąd otrzymujemy równanie
12 + (3r)2 = (2 − r)2.
Rozwiązując to równanie dostajemy dwa rozwiązania
\(r={-1\pm\sqrt{7}\over 4},\)
z których tylko jedno jest dodatnie. Stąd ostatecznie
\(r={-1+\sqrt{7}\over 4}.\)
Zadanie 7
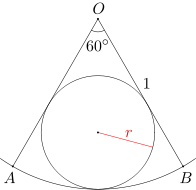
Okrąg o promieniu r jest wpisany w wycinek koła OAB o kącie 60 stopni i promieniu 1, jak pokazano na rysunku. Oblicz r.
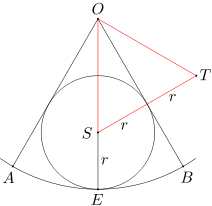
Oznaczmy przez S środek danego okręgu o promieniu r, a przez T punkt symetryczny do punktu S względem prostej OB. Wówczas OS=OT oraz
\(\angle SOT=2\angle SOB=2\cdot 30^\circ=60^\circ.\)
Z równości tych wynika, że trójkąt SOT jest trójkątem równobocznym. Ponadto długość boku ST wynosi 2r, a więc długość boku OS także równa się 2r.
Oznaczmy przez E punkt styczności danego okręgu o promieniu r z łukiem AB. Wówczas długość odcinka OE równa się 1. Stąd uzyskujemy OS+SE=OE, czyli 2r+r=1. A zatem ostatecznie r=1/3.
Zadanie 8
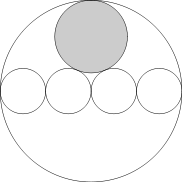
Cztery okręgi, każdy o promieniu 1 są styczne zewnętrznie, jak pokazano na rysunku. Oblicz promień zacieniowanego okręgu.
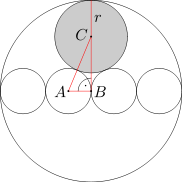
Niech A będzie środkiem tego okręgu o promieniu 1, który jest styczny do zacieniowanego okręgu, B środkiem największego okręgu oraz C środkiem zacieniowanego okręgu. Ponieważ punkt B jest także punktem styczności dwóch danych okręgów o promieniu 1, więc kąt ABC jest prosty.
Długość odcinka AB wynosi 1. Ponieważ promień największego okręgu wynosi 4, więc długość odcinka BC równa się 4-r. Ponadto długość odcinka AC wynosi 1+r. Stąd na mocy twierdzenia Pitagorasa otrzymujemy
AB2 + BC2 = AC2.
Wobec tego
12 + (4 − r)2 = (1 + r)2,
skąd bezpośrednio wyznaczamy r uzyskując r=8/5.
Zadanie 9
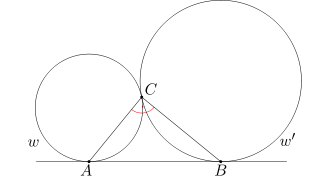
Okręgi w oraz w' są styczne zewnętrznie w punkcie C. Do okręgów tych poprowadzono wspólną styczną zewnętrzną AB (punkty A i B są punktami styczności tej stycznej odpowiednio z okręgami w i w'. Udowodnij, że kąt ACB jest kątem prostym.
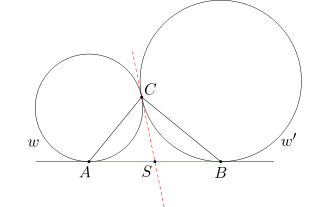
Przez punkt C poprowadźmy prostą, która jest styczna do obu danych okręgów i która przecina odcinek AB w punkcie S. Wówczas SA=SC oraz SB=SC. Stąd wniosek, że punkt S jest środkiem okręgu opisanego na trójkącie ABC. A ponieważ punkt S leży na boku AB, więc trójkąt ABC musi być trójkątem prostokątnym.
Zadanie 10
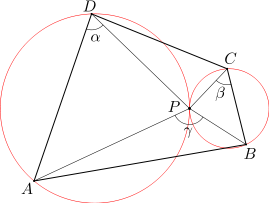
Punkt P leży wewnątrz czworokąta wypukłego ABCD, przy czym miara kąta APB jest równa sumie miar kątów ADP i BCP. Udowodnij, że okręgi opisane na trójkątach ADP i BCP są styczne.
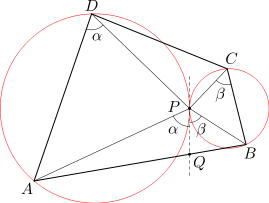
Niech Q będzie takim punktem leżącym na odcinku AB, że miara kąta ADP jest równa mierze kąta APQ. Wówczas z podanej w treści zadania równości kątów wynika, że miara kąta BCP jest równa mierze kąta BPQ.
Wobec tego na mocy twierdzenia o kącie miedzy styczną a cięciwą okrąg opisany na trójkącie ADP jest styczny do prostej PQ. Analogicznie, okrąg opisany na trójkącie BCP jest także styczny do prostej PQ. Stąd wynika, że okręgi opisane na trójkątach ADP i BCP są styczne w punkcie P.
