Najpierw zdefiniowaliśmy potęgę liczby o wykładniku całkowitym dodatnim, następnie rozszerzyliśmy definicję potęgi tak, by wykładnikiem mogła być dowolna liczba całkowita, i wreszcie określiliśmy potęgę, gdy wykładnikiem jest dowolna liczba wymierna. Rozszerzenie zakresu zmienności dla wykładnika potęgi odbywało się kosztem zwężania zakresu zmienności dla podstawy. Ostatnim etapem konstrukcji potęgi o wykładniku rzeczywistym jest określenie jej w przypadku wykładnika niewymiernego. Ten fragment teorii jest trudny i wymaga użycia bardziej złożonych pojęć matematycznych. Dlatego ograniczymy się tutaj do pokazania tylko pewnych intuicji. Chodzi o to, aby nadać znaczenie zapisom takim, jak \(5^{\sqrt{2}}, 5^{\sqrt{3}},\left(\frac{1}{2}\right)^{\pi}\;\) itd.
Wiadomo, że każda liczba niewymierna ma nieskończone rozwinięcie dziesiętne nieokresowe. Na ogół stykamy się z taką sytuacją, że wprawdzie zdajemy sobie sprawę, iż istnieje nieskończony ciąg cyfr rozwinięcia liczby, ale nie potrafimy, bez skomplikowanych rozważań, uzyskać kolejnych cyfr rozwinięcia. Umiemy ewentualnie uzyskać kilka, kilkanaście początkowych cyfr rozwinięcia, np.
- \(\sqrt{2}=1,41421356\ldots\;\)
- \(\sqrt{3}=1,73205080\ldots\;\)
- \(\pi=3,1415926\ldots\;\)
- \(\frac{1}{2\pi}=0,4774648\ldots\;\)
Wyobraźmy sobie zatem, że \(\beta\;\) jest liczbą niewymierną dodatnią i
\(\beta=\alpha_0+0,a_1a_2a_3\ldots,\)
gdzie \(\alpha_0\;\) jest największą liczbą całkowitą mniejszą niż \(\beta\;\), a \(a_1, a_2, a_3, \ldots\;\) są kolejnymi cyframi rozwinięcia liczby \(\beta-\alpha_0\;\).
Niech
\(w_1=\alpha_0+0,a_1=\alpha_0+\frac{a_1}{10}\)
\(w_2=\alpha_0+0,a_1a_2=\alpha_0+\frac{a_1}{10}+\frac{a_2}{10^2}\)
\(w_3=\alpha_0+0,a_1a_2a_3=\alpha_0+\frac{a_1}{10}+\frac{a_2}{10^2}+\frac{a_3}{10^3}\)
i, ogólnie,
\(w_n=\alpha_0+0,a_1a_2\ldots a_n=\alpha_0+\frac{a_1}{10}+\frac{a_2}{10^2}+\ldots+\frac{a_n}{10^n}\; \textrm{ dla} n\in\mathrm{C}_+.\)
Liczby \(w_1, w_2,\ldots\;\) są kolejnymi przybliżeniami dziesiętnymi z niedomiarem liczby \(\beta\;\). Stanowią ciąg niemalejący i ograniczony góry przez liczbę \(\beta\;\) :
\(w_1\leq w_2\leq w_3\leq\ldots\leq w_n\leq w_{n+1}\leq \ldots\)
i dla każdego \(n\in \mathrm{C}_+\;\) prawdziwa jest nierówność \(w_n<\beta\;\).
\((*)\;\) Dla przykładu weźmy \(\beta=\sqrt{2}\;\).
Wówczas
w1 = 1,4
w2 = 1,41
w3 = 1,414
w4 = 1,4142
w5 = 1,41421
Mamy \(w_1\leq w_2\leq w_3\leq w_4\leq w_5\leq \ldots\;\) i każda liczba \(w_n\;\) jest mniejsza niż \(\sqrt{2}\;\).
Niech
\(t_1=\alpha_0+0,a_1+0,1=\alpha_0+\frac{a_1}{10}+\frac{1}{10}\)
\(t_2=\alpha_0+0,a_1a_2+0,01=\alpha_0+\frac{a_1}{10}+ \frac{a_2}{10^2}+\frac{1}{10^2}\)
\(t_3=\alpha_0+0,a_1a_2a_3+0,001=\alpha_0+\frac{a_1}{10}+ \frac{a_2}{10^2}+\frac{a_3}{10^3}+\frac{1}{10^3}\)
i, ogólnie,
\(t_n=\alpha_0+0,a_1a_2\ldots a_n+10^{-n}=\alpha_0+\frac{a_1}{10}+\frac{a_2}{10^2}+ \ldots+\frac{a_n}{10^n}+\frac{1}{10^n} \textrm{dla} n\in\mathrm{C}_+.\)
Liczby \(t_1, t_2,\ldots\;\) są kolejnymi przybliżeniami dziesiętnymi z nadmiarem liczby \(\beta\;\). Stanowią ciąg nierosnący i ograniczony dołu przez liczbę \(\beta\;\)
\(t_1\geq t_2\geq t_3\geq\ldots\geq t_n\geq t_{n+1}\geq \ldots\)
oraz dla każdego \(n\in \mathrm{C}_+\;\) prawdziwa jest nierówność \(t_n>\beta\;\).
\((*)\;\)Wróćmy do przykładu \(\beta=\sqrt{2}\;\).
t1 = 1,4 + 0,1 = 1,5
t2 = 1,41 + 0,01 = 1,42
t3 = 1,414 + 0,001 = 1,415
t4 = 1,4142 + 0,0001 = 1,4143
t5 = 1,41421 + 0,00001 = 1,41422
Mamy \(t_1\geq t_2\geq t_3\geq t_4\geq t_5\geq \ldots\;\) i każda liczba \(t_n\;\) jest większa niż \(\sqrt{2}\;\). Zauważmy, że dla każdego \(n\in\mathrm{C}_+\;\)
\(t_n=w_n+\frac{1}{10^n}, \textrm{czyli} t_n-w_n=\frac{1}{10^n}.\)
Jeśli wyobrazić sobie na osi liczbowej przedziały
\((w_1,t_1), (w_2,t_2),\ldots, (w_n,t_n),\ldots\)
to do każdego z nich należy liczba \(\beta\;\). Można udowodnić, że \(\beta\;\) jest jedyną liczbą, która należy do wszystkich tych przedziałów.
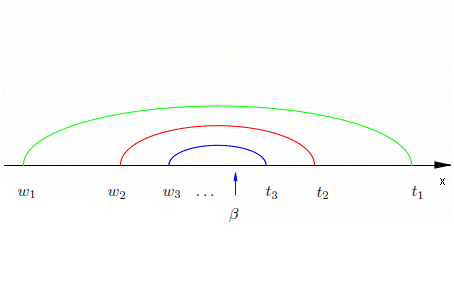
\((*)\;\) W przypadku \(\beta=\sqrt{2}\;\) to liczba \(\sqrt{2}\;\) jest jedyną liczbą rzeczywistą, która należy równocześnie do wszystkich przedziałów
\((1,4;1,5), (1,41;1,42), (1,414;1,415), (1,4142;1,4143), \dots\)
Teraz można próbować zrozumieć, jaka liczba rzeczywista odpowiada symbolowi \(5^{\beta}\;\) (w naszym \((*)\;\) przykładzie \(5^{\sqrt{2}}\;\)).
Ponieważ zarówno liczby \(w_1, w_2,\ldots\;\) jak i liczby \(t_1, t_2,\ldots\;\) są wymierne, to rozumiemy, jaką interpretację mają liczby
\(5^{w_1},5^{w_2},5^{w_3},\ldots \textrm{oraz} 5^{t_1},5^{t_2},5^{t_3},\ldots\)
Można pokazać, że skoro \(w_1\leq w_2\leq w_3\leq\ldots\;\) i \(t_1\geq t_2\geq t_3\geq\ldots\;\), to prawdziwe są nierówności
\(5^{w_1}\leq 5^{w_2}\leq 5^{w_3}\leq\ldots \textrm{i} 5^{t_1}\geq 5^{t_2}\geq 5^{t_3}\geq\ldots\)
oraz, że
\(5^{w_1}<5^{t_1}, 5^{w_2}<5^{t_2}, 5^{w_3}<5^{t_3},\ldots.\)
Dzieje się tak nie tylko dla podstawy \(5\;\), ale dla każdej liczby \(a\;\), która jest większa od liczby \(1\;\). Można sobie te liczby wyobrazić na osi liczbowej.
Można dalej udowodnić, że długości odcinków
\((5^{w_1},5^{t_1}), (5^{w_2},5^{t_2}), (5^{w_3},5^{t_3}),\ldots\)
stają się coraz mniejsze, ,,zmierzają do 0'' i że istnieje tylko jedna liczba, która równocześnie należy do wszystkich tych odcinków. Ta jedna jedyna liczba, która należy do wszystkich odcinków jest właśnie tą liczbą, która odpowiada symbolowi \(5^{\beta}\;\).
Sytuację tę ilustruje poniższy rysunek.
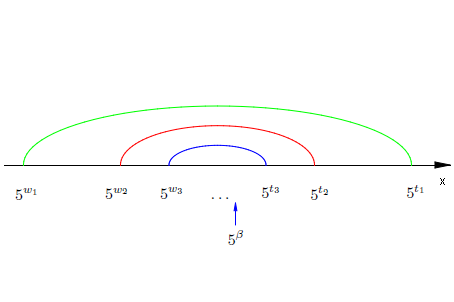
\((*)\;\) W naszym przykładzie w ten sposób nadamy znaczenie symbolowi \(5^{\sqrt{2}}\;\). Jest to jedyna liczba, która należy równocześnie do wszystkich przedziałów
\((5^{1,4},5^{1,5}), (5^{1,41},5^{1,42}), (5^{1,414},5^{1,145}),(5^{1,4142},5^{1,4143}),\ldots\)
Analogiczne rozumowanie dla dowolnej liczby \(a>1\;\) doprowadzi nas do interpretacji symbolu \(a^{\beta}\;\).
W przypadku podstawy \(a\in (0,1)\;\) (np. \(a=\frac{1}{3}\;\)) można powtórzyć całą konstrukcję z tym, że z nierówności \(w_1\leq w_2\leq w_3\leq\ldots\;\) i \(t_1\geq t_2\geq t_3\geq\ldots\;\) wynikają tym razem nierówności
\(a^{t_1}\leq a^{t_2}\leq a^{t_3}\leq\ldots \textrm{i} a^{w_1}\geq a^{w_2}\geq a^{w_3}\geq\ldots\)
oraz
\(a^{t_1}<a^{w_1}, a^{t_2}<a^{w_2}, a^{t_3}<a^{w_3},\ldots.\)
\((*)\;\) Dla przykładu
\(\left(\frac{1}{3}\right)^{t_1}\leq \left(\frac{1}{3}\right)^{t_2}\leq \left(\frac{1}{3}\right)^{t_3}\leq\ldots \textrm{i} \left(\frac{1}{3}\right)^{w_1}\geq \left(\frac{1}{3}\right)^{w_2}\geq \left(\frac{1}{3}\right)^{w_3}\geq\ldots\)
oraz
\(\left(\frac{1}{3}\right)^{t_1}<\left(\frac{1}{3}\right)^{w_1}, \left(\frac{1}{3}\right)^{t_2}<\left(\frac{1}{3}\right)^{w_2}, \left(\frac{1}{3}\right)^{t_3}<\left(\frac{1}{3}\right)^{w_3},\ldots.\)
Symbol \(a^{\beta}\;\) oznacza jedyną liczbę rzeczywistą, która należy do wszystkich przedziałów:
\((a^{t_1},a^{w_1}), (a^{t_2},a^{w_2}), (a^{t_3},a^{w_3}),\ldots\)
\((*)\;\) W naszym przykładzie symbol \(\left(\frac{1}{3}\right)^{\sqrt{2}}\;\) oznacza jedyną liczbę rzeczywistą, która należy do wszystkich przedziałów
\(\left(\left(\frac{1}{3}\right)^{1,5},\left(\frac{1}{3}\right)^{1,4}\right), \left(\left(\frac{1}{3}\right)^{1,42}, \left(\frac{1}{3}\right)^{1,41}\right), \left(\left(\frac{1}{3}\right)^{1,415},\left(\frac{1}{3}\right)^{1,414}\right), \left(\left(\frac{1}{3}\right)^{1,4143}, \left(\frac{1}{3}\right)^{1,4142}\right),\ldots\)
Jeśli \(\beta< 0\;\), to dla podstawy \(a>0\;\) można przyjąć
\(a^{\beta}\stackrel{\textrm{def}}{=}\left(\frac{1}{a}\right)^{-\beta}, \textrm{gdyz} \frac{1}{a}>0 \textrm{i} -\beta>0.\)
Można udowodnić twierdzenie analogiczne do Twierdzenia 5.8.
| Twierdzenie 6.1: |
Niech \(a\;\) i \(b\;\) będą dowolnymi liczbami rzeczywistymi dodatnimi, a \(\gamma\;\) i \(\delta\;\) dowolnymi liczbami rzeczywistymi. Prawdziwe są następujące własności:
|
| Przykład : |
Z Twierdzenia wynikają na przykład równości:
|
