Definicja 5.1. Wielomian \(W(x)\;\) nazywamy podzielnym przez niezerowy wielomian \(U(x)\quad\;\), jeżeli istnieje wielomian \(V(x)\;\) taki, że wielomian \(W(x)\;\) jest iloczynem wielomianów \(U(x)\quad\;\) i \(V(x)\;\), tzn. prawdziwa jest równość wielomianów \(W(x)=U(x)\cdot V(x)\;\).
| Przykłady: |
|
Uwaga 5.1. Z przykładu 2. wynika następujący wniosek.
- Dla dowolnych liczb rzeczywistych \(a\;\) i \(b\;\) oraz liczby całkowitej \(k\;\) większej od \(1\;\) prawdziwa jest równość
\(a^ k-b^ k = (a-b)(a^{k-1}+a^{k-2}b+a^{k-3}b^2+\ldots +ab^{k-2}+b^{k-1}).\;\)
Jest to uogólnienie znanych wzorów na różnicę kwadratów i różnicę sześcianów
\(\begin{array}{rl} a^2-b^2 & =(a-b)(a+b),\\ a^3-b^3 & =(a-b)(a^2+ab+b^2). \end{array}\;\)
Zadanie 5.1. Sprawdzić, czy wielomian \(W(x)\;\) jest podzielny przez \(U(x)\quad\;\), jeśli
- \(W(x) = 2x^3-x^2-5x-2\;\),\(U(x)=x-2\qquad\;\),
- \(W(x) = x^6-1\;\),\(U(x)=x^2-1\quad\;\),
- \(W(x) = 2x^4-3x^3+4x^2-5x+6\;\),\(U(x)=x^2-3x+1\quad\;\),
- \(W(x) = x^6-x-1\;\),\(U(x)=x^3-1\qquad\;\).
Uwaga 5.2. W Zadaniu 5.1. podpunkt 4. wykorzystana została własność, którą warto zapamiętać.
- Jeśli wielomian \(W(x)\;\) jest podzielny przez \(U(x)\quad\;\) i dla pewnej liczby rzeczywistej \(a\;\) \(U(a)=0\;\), to także \(W(a)=0\;\). Istotnie, skoro istnieje wielomian \(V(x)\;\) taki, że \(W(x)=U(x)\cdot V(x)\;\), to\(W(a)=U(a)\cdot V(a)=0\cdot V(a)=0\;\).
W trakcie opisywania własności wielomianów warto zwrócić uwagę na podobieństwa między wielomianami i liczbami całkowitymi. Mówi się o dodawaniu, odejmowaniu i mnożeniu zarówno liczb całkowitych, jak i wielomianów. Definicje podzielności liczb całkowitych, jak i podzielności wielomianów, wyglądają identycznie. Można także przenieść na wielomiany kolejne pojęcie — dzielenie z resztą.
Przypomnijmy
| Twierdzenie 5.1.: |
|
Dla dowolnej liczby całkowitej \(n\;\) i dowolnej liczby całkowitej dodatniej \(m\;\) istnieje tylko jedna para liczb całkowitych \(q\;\), \(r\;\) taka, że
Liczbę \(q\;\) nazywamy ilorazem, a liczbę \(r\;\) resztą. |
| Przykłady: |
|
Sformułujemy odpowiednik tego twierdzenia dla wielomianów w zakresie omawianym w szkole i podamy jego dowód. Następnie podamy, już bez dowodu, ogólną wersję wielomianowego odpowiednika twierdzenia o dzieleniu z resztą.
| Twierdzenie 5.2.: |
|
Dla dowolnego wielomianu \(W(x)\;\) i dowolnej liczby rzeczywistej \(c\;\) istnieją jednoznacznie wyznaczone wielomian \(Q(x)\qquad\;\) i liczba rzeczywista \(r\;\) takie, że |
Uwaga 5.3. Dzielenie z resztą liczby całkowitej przez daną liczbę, jak i dzielenie wielomianu przez dany wielomian, polega na przedstawieniu liczby czy wielomianu w pewnej postaci — postaci opisanej w twierdzeniu. Pomimo słowa "dzielenie" w nazwie do zapisu tych operacji nie używa się symbolu dzielenia.
Zanim zostaną omówione i zademonstrowane różne algorytmy znajdowania ilorazu i reszty w dzieleniu wielomianu przez dwumian, podajemy ważne konsekwencje Twierdzenia 5.2.
| Twierdzenie 5.3.: |
|
Reszta z dzielenia wielomianu \(W(x)\;\) przez dwumian \(x-c\;\) jest równa wartości wielomianu \(W(x)\;\) dla \(x=c\;\), tzn. liczbie \(W(c)\quad\;\). |
| Twierdzenie 5.4.: |
|
Jeżeli w dzieleniu wielomianu \(W(x)\;\) przez dwumian \(x-c\;\) reszta z dzielenia jest równa 0, to wielomian \(W(x)\;\) jest podzielny przez dwumian \(x-c\;\). |
| Twierdzenie 5.5. (Bézouta): |
|
Liczba \(c\;\) jest pierwiastkiem wielomianu \(W(x)\;\) wtedy i tylko wtedy, gdy wielomian \(W(x)\;\) jest podzielny przez dwumian \(x-c\;\). |
Teraz omówione zostaną algorytmy pozwalające wyznaczyć iloraz oraz resztę w dzieleniu \(W(x)\;\) przez dwumian \(x-c\;\).
Odpowiedź na pytanie jak praktycznie znaleźć iloraz i resztę w dzieleniu wielomianu \(W(x)\;\) przez dwumian \(x-c\;\) ukryta jest w równości \(W(x)=(x-c)Q(x)+r\;\), a także w rozwiązaniu Zadania 5.1. podpunkt 1. Sposób wyznaczania wielomianu \(Q(x)\qquad\;\) i liczby \(r\;\) pokazujemy jeszcze raz w rozwiązaniu kolejnego zadania.
Zadanie 5.2. (jak dzielimy z resztą wielomian przez dwumian - METODA I) Podziel z resztą wielomian \(W(x)=x^4-2x^3+4x^2+1\;\) przez dwumian \(x-2\;\).
Rozwiązanie: Zgodnie z Twierdzeniem 5.2. szukamy wielomianu \(Q(x)=ax^3+bx^2+cx+d\;\), gdzie \(a,b,c,d\;\) są liczbami rzeczywistymi, oraz liczby \(r\;\) takich, że zachodzi równość wielomianów
\(\begin{array}{rl} x^4-2x^3+4x^2+1 & = (ax^3+bx^2+cx+d)(x-2)+r=\\ & = ax^4+x^3(-2a+b) +x^2(-2b+c)+x(-2c+d)-2d+r. \end{array}\;\)
Z porównania współczynników otrzymujemy układ równań
\({\left\{ \begin{array}{rl} 1=a \\ -2=-2a+b\\ 4=-2b+c \\ 0 = -2c+d \\ 1 = -2d+r. \end{array} \right.}\;\)
Stąd \(a=1\;\), \(b=-2+2=0\;\), \(c=4\;\), \(d=8\;\), \(r=17\;\). Zatem
\(x^4-2x^3+4x^2+1 = (x^3+4x+8)(x-2)+17.\;\)
Omówiony poniżej schemat Hornera jest uogólnieniem metody opisanej w rozwiązaniu Zadania 5.2. Podaje się w nim wzory na wszystkie współczynniki ilorazu wielomianu \(W(x)\;\) przez dwumian \(x-c\;\) oraz wzór na resztę.
Schemat Hornera (jak dzielimy z resztą wielomian przez dwumian — METODA II).
Niech \(W(x)=a_ nx^ n+a_{n-1}x^{n-1}+\ldots +a_1x+a_0\;\) będzie wielomianem stopnia \(n\;\) i niech \(c\;\) będzie ustaloną liczbą rzeczywistą. Szukamy wielomianu \(Q(x)\qquad\;\) i takiej liczby \(r\;\), że
\(W(x) = (x-c)\cdot Q(x) +r.\;\)
Z Twierdzenia 2.2. wielomian \(Q(x)\qquad\;\) jest stopnia \(n-1\;\). Ma zatem postać
\(Q(x) = b_{n-1}x^{n-1}+b_{n-2}x^{n-2}+\ldots +b_1x+b_0.\;\)
Powinna być spełniona równość:
\(\begin{array}{rl} W(x) & = (x-c)Q(x)+r=\\ & = (x-c)(b_{n-1}x^{n-1}+b_{n-2}x^{n-2}+\ldots +b_1x+b_0)+r=\\ & = b_{n-1}x^ n+(b_{n-2}-cb_{n-1})x^{n-1} +(b_{n-3}-cb_{n-2})x^{n-2}+\ldots +\\ & \quad +(b_1-cb_2)x^2+(b_0-cb_1)x-cb_0+r. \end{array}\;\)
Porównując współczynniki otrzymanego właśnie wielomianu i wielomianu \(W(x)\;\), otrzymujemy układ równań
\({\left\{ \begin{array}{rl} b_{n-1}=a_ n\\ b_{n-2}-cb_{n-1}=a_{n-1}\\ b_{n-3}-cb_{n-2}=a_{n-2}\\ \vdots \\ b_1-cb_2 = a_2\\ b_0-cb_1=a_1\\ r-cb_0=a_0, \end{array} \right.}\;\)
który może być zapisany następująco:
\(\begin{array}{rl}(\ast ){\left\{ \begin{array}{rl} b_{n-1}=a_ n\\ b_{n-2}=cb_{n-1}+a_{n-1}\\ b_{n-3}=cb_{n-2}+a_{n-2}\\ \vdots \\ b_1=cb_2 + a_2\\ b_0=cb_1+a_1\\ r=cb_0+a_0. \end{array} \right.} \end{array}\;\)
Układ równań pozwala wyliczyć wszystkie współczynniki \(b_{n-1},b_{n-2},\ldots,b_1,b_0\;\) oraz \(r\;\), gdy dane są współczynniki \(a_ n,a_{n-1},\ldots,a_1,a_0\;\).
Obliczanie współczynników wielomianu \(Q(x)\qquad\;\) oraz reszty z dzielenia ułatwia dwuwierszowa tabela, w której w pierwszym wierszu wypisuje się współczynniki wielomianu \(W(x)\;\), a w drugim współczynniki wielomianu \(Q(x)\qquad\;\) oraz resztę \(r\;\).
| \(a_n\;\) | \(a_{n-1}\;\) | \(a_{n-2}\;\) | … | \(a_2\;\) | \(a_1\;\) | \(a_0\;\) | |
| \(c\;\) | \(a_n\! =\! b_{n-1}\quad\;\) | \(cb_{n-1}\! +\! a_{n-1}\! =\! b_{n-2}\;\) | \(cb_{n-2}\! +\! a_{n-2}\! =\! b_{n-3}\;\) | … | \(cb_2\! +\! a_2\! =\! b_1\;\) | \(cb_1\! +\! a_1\! =\! b_0\quad\;\) | \(cb_0\! +\! a_0\! =\! r\;\) |
| \(\underbrace{\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad }\;\) | \(\underbrace{\qquad \qquad \quad }\;\) | ||||||
| to są współczynniki wielomianu \(Q(x)\qquad\;\) | to jest \(r\;\), | ||||||
| czyli \(W(c)\;\) | |||||||
Powyższą tabelę, czyli układ \((\ast )\;\) nazywamy schematem Hornera.
Zadanie 5.3. Stosując schemat Hornera znaleźć iloraz i resztę przy dzieleniu wielomianu\(W(x) = x^3-3x-2\;\) przez
- dwumian \(x-3\;\),
- dwumian \(x+1\;\).
Uwaga 5.4. Przy wpisywaniu współczynników wielomianu \(W(x)\;\) do tabeli musimy pamiętać, iż każda potęga zmiennej ma swoje "miejsce" w tabeli i jeśli któryś ze współczynników wielomianu \(W(x)\;\) jest równy \(0\;\), to ten współczynnik musi być także zapisany w tabeli.
Uwaga 5.5. Schemat Hornera jest szybkim algorytmem obliczania wartości wielomianu dla określonej liczby. Możemy go wykorzystać w zadaniach podobnych do Zadań 4.3. – 4.6. Odniesiemy przy tym korzyść podwójną, bo uzyskamy również współczynniki ilorazu. Rozwiązanie poniższego zadania pokazuje, w jaki sposób można to wykorzystać.
Zadanie 5.4. Znaleźć wszystkie pierwiastki wielomianu
\(W(x) = 2x^4-2x^3-3x^2-x-2.\;\)
Dzielenie "pisemne" (jak dzielimy z resztą wielomian przez dwumian — METODA III
Opisany poniżej algorytm przypomina algorytm pisemnego dzielenia liczb naturalnych.
Niech \(W(x) = a_ nx^ n+a_{n-1}x^{n-1}+\ldots +a_1x+a_0\;\) i niech \(c\;\) będzie ustaloną liczbą rzeczywistą. Zauważmy, że
\(\begin{array}{rl} W(x) -a_ nx^{n-1}(x-c) & = (a_ nx^ n+a_{n-1}x^{n-1}+\ldots +a_1x+a_0)-(a_ nx^ n-a_ ncx^{n-1})=\\ & = (a_{n-1}+a_ nc)x^{n-1}+a_{n-2}x^{n-2}+\ldots +a_1x+a_0. \end{array}\;\)
Oznaczamy
\((a_{n-1}+a_ nc)x^{n-1}+a_{n-2}x^{n-2}+\ldots +a_1x+a_0 = R_1(x).\;\)
Wówczas
\(W(x) = a_ nx^{n-1}(x-c)+R_1(x).\;\)
Jeśli \(R_1(x)\;\) nie jest wielomianem stałym, to powtarzamy "dzielenie z resztą" w stosunku do \(R_1(x)\;\) i \(x-c\;\). Operację tę powtarzamy tak długo, aż ostatni z otrzymanych w ten sposób wielomianów \(R_i(x)\;\) będzie wielomianem stałym.
\(\begin{array}{rl} W(x) & = a_ nx^{n-1}(x-c)+R_1(x)=\\ & = a_ nx^{n-1}(x-c)+a'_{n-1}x^{n-2}(x-c)+R_2(x)=\ldots =\\ & = a_ nx^{n-1}(x-c)+a'_{n-1}x^{n-2}(x-c)+a''_{n-2}x^{n-3}(x-c)+R_3(x)=\\
& = a_nx^{n-1}(x-c)+a'_{n-1}x^{n-2}(x-c)+a''_{n-2}x^{n-3}(x-c)+\ldots+R_n(x)\\
& = (x-c)(a_ nx^{n-1}+a'_{n-1}x^{n-2}+a''_{n-2}x^{n-3}+\ldots) +R_n(x)=\\ & = (x-c)Q(x)+R_n(x). \end{array}\;\)
\(Q(x)\qquad\;\) jest ilorazem, a \(R_n(x)=r\;\) jest wielomianem stopnia 0 (\(r\ne 0\;\) ) lub wielomianem zerowym (\(r=0\;\) ).
Ponieważ \(a_ nx^{n-1}\;\) możemy traktować jako iloraz \(a_ nx^ n\;\) przez \(x\;\), a więc iloraz jednomianów z najwyższymi potęgami zmiennej w wielomianach \(W(x)\;\) i \(x-c\;\), całą tę operację możemy zapisywać podobnie jak w pisemnym dzieleniu liczb całkowitych w postaci
\(\begin{array}{rl}& \underline{a_ nx^{n-1}\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \quad \quad}\\ & a_ nx^ n+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\ldots +a_1x+a_0\, :\, x-c\\ -\quad & \! \! \underline{(a_ nx^ n-ca_ nx^{n-1})}\\ & (a_{n-1}\! +\! ca_ n)x^{n-1}+a_{n-2}x^{n-2}+\ldots +a_1x+a_0 \end{array}\;\)
W pierwszym wierszu pod kreską piszemy wielomian \(W(x)\;\). Iloraz "z dzielenia" jednomianów \(a_ nx^ n\;\) i \(x\;\) zapisujemy nad kreską. Następnie mnożymy otrzymany iloraz \(a_ nx^{n-1}\;\) przez \(x-c\;\) i zapisujemy go w drugim wierszu pod kreską, po czym odejmujemy otrzymany iloczyn od wielomianu \(W(x)\;\). Różnicę zapisujemy pod druga kreską. Czynności te powtarzamy w stosunku do otrzymanej różnicy.
Niektórzy zalecają zamiast odejmowania kolejnych iloczynów zapisywanie ich od razu z przeciwnym znakiem i dodawanie. Taka operacja zapobiega błędom rachunkowym. Zapis wówczas wygląda następująco:
\(\begin{array}{rl}& \underline{\quad a_ nx^{n-1}\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad}\\ & \quad (a_ nx^ n+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\ldots +a_1x+a_0)\, :\, (x-c)\\ + &\, \, \, \underline{\, -a_ nx^ n+ca_ nx^{n-1}}\\ & \quad \, (a_{n-1}\! +\! ca_ n)x^{n-1}+a_{n-2}x^{n-2}+\ldots +a_1x+a_0 \end{array}\;\)
Zadanie 5.5. Wykonać dzielenie z resztą wielomianu \(W(x)=x^4-2x^3+4x^2-6x+8\;\) przez dwumian \(x-1\;\).
Zadanie 5.6. Wykonać dzielenie z resztą wielomianu \(W(x)=2x^5-5x^3+8x\;\) przez dwumian \(x+3\;\).
Zadanie 5.7. Wykonać dzielenie z resztą wielomianu \(W(x)=x^5-4x^3+6x^2-8x+10\;\) przez dwumian \((2x-4)\;\).
Uwaga 5.6. W rozwiązaniu Zadania 5.7 mogliśmy najpierw wykonać dzielenie dla wielomianu \(W(x)\;\) i dwumianu \(x-2\;\), ponieważ \(2x-4=2(x-2)\;\), a następnie otrzymany iloraz pomnożyć przez \(\frac{1}{2}\;\). Tak otrzymane iloraz i reszta są identyczne z wyliczonymi. Dlaczego? Tę kwestię wyjaśnia rachunek:
\(\begin{array}{rl} x^5-4x^3+6x^2-8x+10 & = (2x-4)\bigg(\frac{1}{2}x^4+x^3+3x+2\bigg)+18=\\ & = (x-2)\cdot 2\bigg(\frac{1}{2}x^4+x^3+3x+2\bigg)+18=\\ & = (x-2)(x^4+2x^3+6x+4)+18 \end{array}\;\)
Uwaga 5.7. W każdym z omówionych algorytmów iloraz \(Q(x)\qquad\;\) i reszta \(r\;\) są wyznaczone jednoznacznie.
Uwaga 5.8. Algorytm "pisemnego" dzielenia z resztą wielomianu przez dwumian, podobnie jak dodawanie, odejmowanie i mnożenie wielomianów, można opisać bez używania zmiennej \(x\;\). Na przykład, operację dzielenia z pierwszego przykładu można opisać następująco:
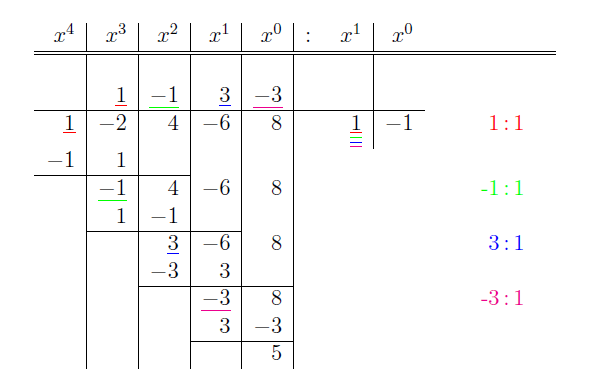
Stąd
![]()
Prawdziwe jest ogólne twierdzenie
| Twierdzenie 5.6 (o dzieleniu z resztą dla dowolnych wielomianów): |
|
Dla dowolnego wielomianu \(W(x)\;\) i dowolnego niezerowego wielomianu \(U(x)\quad\;\), istnieje tylko jedna para wielomianów \(Q(x)\qquad\;\) i \(R(x)\;\) taka, że
|
Dowód twierdzenia pomijamy.
Uwaga 5.9. Opisane METODA I i METODA III dzielenia z resztą dla wielomianu \(W(x)\;\) i dwumianu \(x-c\;\) przenoszą się na dowolne wielomiany. Zilustrujemy ten fakt na przykładach.
Przykład 5.1. Wykonać dzielenie z resztą wielomianu \(W(x)=2x^4-3x^3+4x^2-5x+6\;\) przez \(U(x)=x^2-3x+1\;\).
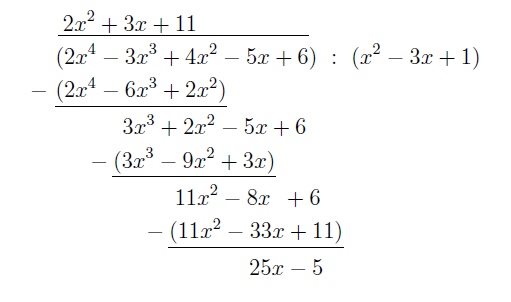
Tak, jak poprzednio, za każdym razem "dzielimy" jednomian z najwyższą potęgą zmiennej dzielnej przez jednomian z najwyższą potęgą zmiennej dzielnika. Stąd
\(2x^4-3x^3+4x^2-5x+6=(x^2-3x+1)(2x^2+3x+11)+25x-5.\;\)
i \(Q(x) = 2x^2+3x+11\;\) oraz \(R(x) = 25x-5\;\).
Drugi sposób wynika z tego, że zgodnie z Twierdzeniem 2.2. stopień wielomianu \(Q(x)\qquad\;\) jest równy różnicy stopni wielomianów \(W(x)\;\) i \(U(x)\quad\;\), zaś \(R(x)\;\) jest wielomianem zerowym lub jego stopień jest mniejszy od stopnia wielomianu \(U(x)\quad\;\). Wśród takich wielomianów szukamy wielomianów \(Q(x)\qquad\;\) i \(R(x)\;\), wyznaczając ich współczynniki z równości \(W(x)=Q(x)U(x)+R(x)\;\). Zilustrujemy tę metodę na przykładzie.
Przykład 5.2. Podzielić z resztą wielomian \(W(x)=x^3-3x^2-x-1\;\) przez wielomian\(U(x)=3x^2-2x+1\;\). Ponieważ \(\mathrm{st}\, W(x)=3\;\) i \(\mathrm{st}\, U(x)=2\;\), więc \(\mathrm{st}\, Q(x)=1\;\) natomiast \(R(x)=0\;\) lub \(\mathrm{st}\, R(x)<2\;\). Zatem
\(Q(x) = ax+b \qquad \mathrm{i} \qquad R(x)=cx+d.\;\)
Z równości
\(x^3-3x^2-x-1 = (3x^2-2x+1)(ax+b)+cx+d\;\)
otrzymujemy
\(x^3-3x^2-x-1 = 3ax^3+(3b-2a)x^2+(-2b+a+c)x+b+d.\;\)
Porównując współczynniki, mamy
\({\left\{ \begin{array}{rl} 1=3a\\ -3=3b-2a\\ -1=-2b+a+c\\ -1=b+d. \end{array} \right.}\;\)
Stąd \(a=\frac{1}{3}\;\), \(b=-\frac{7}{9}\;\), \(c=-\frac{26}{9}\;\), \(d=-\frac{2}{9}\;\), czyli \(Q(x)=\frac{1}{3}x-\frac{7}{9}\;\) i \(R(x)=-\frac{26}{9}x-\frac{2}{9}\;\) oraz
\(x^3-3x^2-x-1 = (3x^2-2x+1)\bigg(\frac{1}{3}x-\frac{7}{9}\bigg)-\frac{26}{9}x-\frac{2}{9}.\;\)
Przykład 5.3. Podzielić z resztą wielomian \(W(x)=x^3+2x^2+1\;\) przez wielomian \(U(x)=x^4-2x+2\;\).
Zauważmy, że \(\mathrm{st}{W(x)}=3\;\), \(\mathrm{st}U(x)=4\;\) i \(\mathrm{st}{W(x)}<\mathrm{st}{U(x)}\;\). Zatem
\(
W(x) = U(x) \cdot 0 +W(x),
\;\)
czyli \(Q(x)=0\;\) i \(R(x)=W(x)\;\).
Uwaga 5.10. Przedstawienie wielomianu \(W(x)\;\) w postaci iloczynu wielomianów stopni dodatnich nazywamy rozkładem wielomianu na czynniki. Operacja rozkładu wielomianu na czynniki jest niezwykle użyteczna przy rozwiązywaniu równań i nierówności wielomianowych. Rozkład na czynniki związany jest więc z poszukiwaniem jego dzielników, tzn. wielomianów stopni dodatnich, przez które wielomian jest podzielny. W czynności tej można wykorzystać wzory skróconego mnożenia, operacje wyłączania czynnika przed nawias oraz twierdzenie Bézouta.
Zilustrujemy to w rozwiązanich kilku zadań
Zadanie 5.8. Rozłożyć na czynniki wielomian \(W(x)=x^8-1\;\).
Zadanie 5.9. Rozłożyć na czynniki wielomian \(W(x)=2x^5-5x^3-3x\;\).
Zadanie 5.10. Rozłożyć na czynniki wielomian \(W(x)=x^5-5x^4+7x^3-2x^2+4x-8\;\).
Ogólnie, jeśli \(a\;\) jest pierwiastkiem wielomianu \(W(x)\;\), to możemy napisać \(W(x)=(x-a)Q(x)\;\), a następnie powtórzyć całą operację rozkładania na czynniki dla wielomianu \(Q(x)\qquad\;\).
Na zakończenie przytoczymy główne twierdzenie o rozkładzie wielomianu na czynniki (bez dowodu).
| Twierdzenie 5.7.: |
|
Każdy wielomian o wspólczynnikach rzeczywistych stopnia dodatniego bądź nie daje się rozłożyć na czynniki, bądź jest iloczynem wielomianów stopni dodatnich, z których żaden nie daje się rozłożyć na czynniki. |
| Twierdzenie 5.8: |
|
Jedynymi wielomianami o wspólczynnikach rzeczywistych stopni dodatnich, które nie dają się rozłożyć na czynniki, są wielomiany pierwszego stopnia oraz trójmiany kwadratowe o wyróżniku ujemnym. |
Poniższy przykład pokazuje, że można wskazać wielomian, który nie ma pierwiastków i nie jest trójmianem kwadratowym.
Przykład 5.4.: Niech \(W(x)=x^4+4\;\). Wielomian ten przyjmuje tylko wartości dodatnie, więc nie ma pierwiastków. Zauważmy, że
\(x^4+4 = x^4+4x^2+4-4x^2 = (x^2+2)^2-(2x)^2 = (x^2+2+2x)(x^2+2-2x).\;\)
Wielomian \(W(x)\;\) jest iloczynem dwóch trójmianów kwadratowych o wyróżnikach ujemnych.
