Odcinek AB ma długość 425 km. Po prostej AB poruszają się z prędkością jednostajną dwa ciała. Pierwsze w pewnej chwili mija punkt B i kieruje się w stronę punktu A. Godzinę później drugie ciało mija punkt A i porusza się w kierunku punktu B. Ciała te spotykają się w odległości 126 km od punktu A. Prędkość drugiego ciała jest o 36 km/h mniejsza od prędkości drugiego ciała. Oblicz prędkości obu ciał.
Rozwiązanie.
Zadanie to na pozór nie różni się istotnie od poprzedniego. Rozwiążemy je metodą podobną do poprzedniej, tzn. za pomocą układu równań z dwiema niewiadomymi v i t:
-
-
v prędkość (w km/h) drugiego ciała, t czas (w godzinach) poruszania się drugiego ciała, v + 36 prędkość pierwszego ciała, t + 1 czas poruszania się pierwszego ciała.
-
Mamy zatem układ równań:
-
- vt = 126
- (v + 36)(t + 1) = 299
Przekształcając ten układ równań, można zeń wyprowadzić równanie kwadratowe 36t2 − 137t + 126 = 0. Oto szczegóły:
-
- vt = 126
- vt + v + 36t + 36 = 299
Podstawiając vt = 126 do drugiego równania, otrzymujemy równanie liniowe
-
- 126 + v + 36t + 36 = 299,
czyli
-
- v = 137 − 36t.
Podstawiając tę wartość v do pierwszego równania, otrzymujemy po uporządkowaniu
-
- 36t2 − 137t + 126 = 0.
To równanie kwadratowe ma dwa rozwiązania: \(t_1 = \frac{14 }{ 9}\) i \(t_2 = \frac{9 }{ 4}\). Stąd dostajemy
-
- \((v_A = 81, \quad v_B = 117)\qquad\) lub \(\qquad (v_A = 56, \quad v_B = 92)\)
(vA i vB oznaczają tu prędkości obu ciał; vA – prędkość ciała, które zmierza od punktu A w kierunku punktu B, vB – prędkość drugiego ciała).
Dlaczego są dwa rozwiązania?
Dziwić może to, że otrzymaliśmy dwa rozwiązania. Spróbujmy obliczyć, w jakiej odległości od punktu A spotkają się te ciała w zależności od prędkości v, z jaką porusza się ciało zmierzające od punktu A w kierunku punktu B. Czas t do spotkania obliczymy z równania
-
- vt + (v + 36)(t + 1) = 425.
Otrzymamy
-
- \( t = \frac{389 - v }{ 2v + 36}. \)
Poszukiwana droga wynosi wtedy
-
- \( f(v) = \frac{v(389 - v) }{ 2(v + 18)}. \)
Nietrudno zauważyć, że ten wzór ma sens dla \(v \in \langle 0,389 \rangle\). Wykres funkcji f wygląda następująco (na wykresie zaznaczone są dane z zadania):
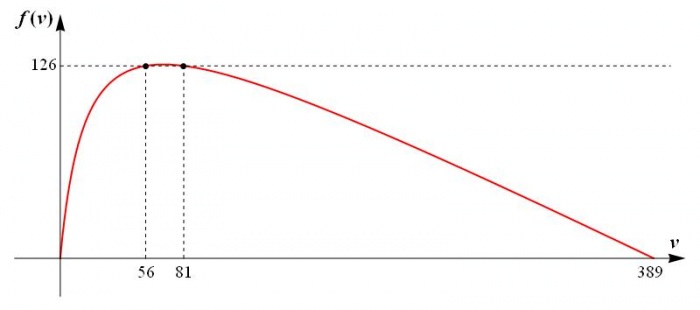
Teraz już nie powinno dziwić to, że są dwa rozwiązania.
Komentarz
Oczywiście zadanie można próbować rozwiązywać metodą przeszukiwania.
-
- Jeden sposób polega na przeszukiwaniu kolejno wszystkich całkowitych wartości v.
- Drugi polega na stosowaniu metody kolejnych przybliżeń.
Nie będę tu omawiał wszystkich szczegółów tych metod. Zauważę tylko, że nie musi dla ucznia być oczywiste to, że zadanie ma dwa rozwiązania; może się okazać, że uczeń zaprzestanie dalszych poszukiwań po znalezieniu pierwszego rozwiązania. Pamiętajmy też o tym, że znaleziona wyżej funkcja f nie jest monotoniczna, a rozwiązania zadania leżą blisko jej maksimum. Ten brak monotoniczności, który uczeń może zaobserwować, może utrudnić poszukiwania i sprawić, że uczeń zrezygnuje przed znalezieniem jakiegokolwiek rozwiązania.
Ostatnie zadanie pokazuje jednak, że problem jednoznaczności rozwiązania nie jest problemem sztucznym. Rozwiązanie tego zadania, w którym zostanie znaleziona tylko jedna para prędkości (np. 56 km/h i 92 km/h) z całą pewnością nie jest kompletne. Gdyby takie zadanie rozwiązywał gimnazjalista, to z całą pewnością uznałbym rozwiązanie za duże osiągnięcie. Tym bardziej, że gimnazjalista nie dysponuje środkami pozwalającymi mu rozwiązać to zadanie dokładnie. Natomiast od maturzysty muszę wymagać więcej. Jeśli maturzysta zdecyduje się w jakimś zadaniu zastosować metodę prób i błędów (czy kolejnych przybliżeń), musi wykazać, że zadanie ma dokładnie jedno rozwiązanie. Zadanie 13 nie różni się na pierwszy rzut oka od Zadania 12 tak bardzo, by dostrzec, że jedno z nich ma rozwiązanie jednoznaczne, a drugie ma dwa rozwiązania.
Zatem rozwiązania Zadania 12 metodą prób i błędów są niekompletne; z matematycznego punktu widzenia nie są więc całkowicie poprawne.
