Dziadek Grzesia ma 5 razy tyle lat, ile tata Grzesia miał wtedy, kiedy dziadek miał tyle lat, ile tata ma teraz. Dziadek i tata Grzesia mają razem 136 lat. Ile lat ma dziadek Grzesia i ile lat ma tata Grzesia?
Omówię rozwiązanie graficzne. Długością odcinków wyrażę ważne wielkości występujące w zadaniu. Długość odcinka AB to obecny wiek dziadka. Długość odcinka AC to obecny wiek taty Grzesia. Długość odcinka CB to różnica wieku dziadka i taty.
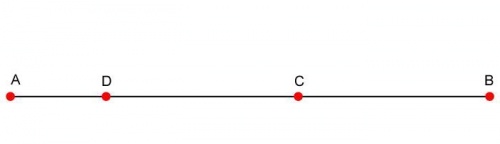
Ta różnica to wielkość, która ma duże znaczenie w zadaniu. Zastanówmy się, kiedy dziadek miał tyle lat, ile tata ma teraz. Otóż było to tyle lat temu, ile właśnie wynosi ta różnica wieku. A wtedy tata miał o tyle lat mniej. Wiek taty Grzesia wtedy to długość odcinka AD; odcinki DC i CB mają równe długości. O tyle lat bowiem tata był młodszy, o ile młodszy był dziadek.
W tym zadaniu mamy dwie podstawowe wielkości nieznane: wiek dziadka Grzesia i wiek taty Grzesia. Mamy też dwa warunki wiążące te dwie wielkości nieznane. Pierwszy warunek jest łatwy do odczytania w treści zadania: razem mają 136 lat. Drugi warunek jest bardziej skomplikowany. Aby go dobrze zrozumieć, nazwijmy dwa momenty, o których mowa w zadaniu. Pierwszy z nich, to TERAZ, czyli dzisiaj. Dziadek ma pewną liczbę lat, tata Grzesia jest od dziadka sporo młodszy. Drugi moment nazwiemy WTEDY; jest to ten moment, w którym dziadek Grzesia był sporo młodszy i miał dokładnie tyle lat, ile tata Grzesia ma dzisiaj. Tata Grzesia był wtedy też młodszy; oczywiście o tyle samo lat, o ile młodszy był dziadek Grzesia. Drugi warunek mówi, że wiek dziadka TERAZ jest 5 razy większy od wieku taty WTEDY. Mamy dwie wielkości nieznane i dwa warunki. Możemy więc ułożyć co najmniej cztery równania. Omówimy dokładnie wszystkie cztery, by pokazać różne sposoby wykorzystania tego skomplikowanego warunku "TERAZ-WTEDY".
Sposób B1. Niewiadomą x będzie wiek dziadka Grzesia TERAZ (wyrażony w latach). Wiek taty Grzesia (także wyrażony w latach) wyznaczymy z pierwszego warunku, a drugi warunek zapiszemy jako równanie. Mamy zatem:
-
-
x wiek dziadka Grzesia TERAZ, 136 − x wiek taty Grzesia TERAZ, 136 − x wiek dziadka Grzesia WTEDY, x − (136 − x) tyle lat minęło od WTEDY do TERAZ, (136 − x) − (x − (136 − x)) wiek taty Grzesia WTEDY.
-
Otrzymujemy równanie
-
- \(x = 5 \cdot [ (136 - x) - ( x - (136-x) ) ], \)
którego rozwiązaniem jest x = 85. Zatem dziadek Grzesia ma teraz 85 lat, a tata Grzesia ma w takim razie 51 lat.
Sposób B2. Niewiadomą x będzie wiek dziadka Grzesia TERAZ (wyrażony w latach). Wiek taty Grzesia (także wyrażony w latach) wyznaczymy tym razem z drugiego warunku, a pierwszy warunek zapiszemy jako równanie. Korzystamy tu z dokonanej wyżej obserwacji, że tata Grzesia WTEDY był o tyle samo lat młodszy, o ile młodszy był dziadek Grzesia. A zatem wiek dziadka Grzesia WTEDY (czyli wiek taty Grzesia TERAZ) leży dokładnie pośrodku odcinka od wieku taty WTEDY do wieku dziadka TERAZ. Mamy zatem:
-
-
x wiek dziadka Grzesia TERAZ, \(\frac{1 }{ 5}x\) wiek taty Grzesia WTEDY, \(\frac{4 }{ 5}x\) tyle lat dzieli wiek taty WTEDY i wiek dziadka TERAZ, \(\frac{2 }{ 5}x\) tyle lat minęło od WTEDY do TERAZ, \(\frac{1 }{ 5}x + \frac{2 }{ 5}x\) wiek taty Grzesia TERAZ.
-
Otrzymujemy równanie
-
- \( x + \frac{1 }{ 5}x + \frac{2 }{ 5}x = 136,\)
którego rozwiązaniem jest x = 85. Zatem dziadek Grzesia ma teraz 85 lat, a tata Grzesia ma w takim razie 51 lat.
Sposób B3. Niewiadomą x będzie wiek taty Grzesia TERAZ (wyrażony w latach). Wiek dziadka Grzesia (także wyrażony w latach) wyznaczymy z pierwszego warunku, a drugi warunek zapiszemy jako równanie. Mamy zatem:
-
-
x wiek taty Grzesia TERAZ, 136 − x wiek dziadka Grzesia TERAZ, x wiek dziadka Grzesia WTEDY, 136 − 2x tyle lat minęło od WTEDY do TERAZ, x − (136 − 2x) wiek taty Grzesia WTEDY.
-
Otrzymujemy równanie
-
- \(136 - x = 5 \cdot \bigl ( x - (136-2x) \bigr ), \)
którego rozwiązaniem jest x = 51. Zatem tata Grzesia ma teraz 51 lat, a dziadek Grzesia ma w takim razie 85 lat.
Niewiadomymi będą obie wielkości nieznane: wiek dziadka dzisiaj i wiek taty dzisiaj (oba wyrażone w latach). Oba warunki zostaną zapisane w postaci równań. Mamy zatem:
-
-
x wiek dziadka Grzesia TERAZ, y wiek taty Grzesia TERAZ, y wiek dziadka Grzesia WTEDY, x − y tyle lat minęło od WTEDY do TERAZ, y − (x − y) wiek taty Grzesia WTEDY.
-
Otrzymujemy układ równań
-
- \(x + y = 136; \qquad x = 5 ( y - (x-y) )\)
którego rozwiązaniem jest
-
- \(x = 85; \qquad y = 51\)
Zatem dziadek Grzesia ma teraz 85 lat, a tata Grzesia 51 lat.
