Związki pomiędzy kwantyfikatorami \(\forall,\exists\) obrazuje tzw. kwadrat Arystotelesa. Poniżej jest on zaprezentowany w rozszerzonej formie, tzw. sześciokąta logicznego:
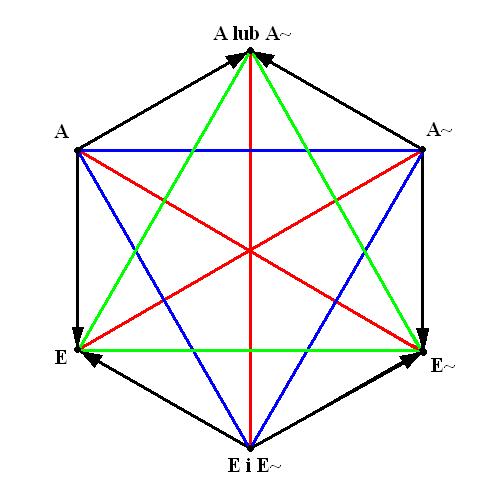
Załóżmy, że mówimy o jakiś obiektach, na przykład jabłkach w jakimś koszyku. Dodatkowo, załóżmy że w danym koszyku istotnie są jakieś jabłka - przynajmniej jedno. Niech Z(x) oznacza, że jabłko x jest zielone. Możemy interpretować powyższy sześciokąt w następujący sposób:
- A - \(\forall_x Z(x)\) - każde jabłko jest zielone,
- A~ - \(\forall_x \lnot Z(x)\) - każde jabłko nie jest zielone,
- E - \(\exists_x Z(x)\) - istnieje jabłko które jest zielone,
- E~ - \(\exists_x \lnot Z(x)\) - istnieje jabłko które nie jest zielone.
Przy tej interpretacji:
- Strzałki oznaczają implikacje - na przykład \(\forall_x Z(x)\Rightarrow \exists_x W(x)\): jeśli każde jabłko jest zielone, to też istnieje zielone jabłko.
- Czerwone linie oznaczają pary zdań z których prawdziwe jest zawsze dokładnie jedno - na przykład albo każde jabłko jest zielone albo istnieje jabłko które nie jest zielone.
- Niebieskie linie oznaczają pary zdań sprzecznych - na przykład nie może być tak, że jednocześnie każde jabłko jest zielone i jednocześnie każde nie jest zielone.
- Zielone linie oznaczają pary zdań które nie mogą być jednocześnie fałszywe - na przykład nie może być tak, że ani nie ma zielonego jabłka, ani nie ma jabłka które by nie było zielone.
Ważne jest założenie, że w rozpatrywanym koszyku są pewne jabłka. Gdyby bowiem żadnych jabłek nie było, prawdą było by zdanie:
- Każde jabłko w tym koszyku jest zielone i jednocześnie każde jabłko w tym koszyku nie jest zielone.
Czyli pisząc formalnie \(\left(\forall_x Z(x)\right)\wedge\left(\forall_x \lnot Z(x)\right)\).
